Статистический образ мышления. Научная публикация. (Лекция 3)

Основные выводы
предыдущих лекций
Научная публикация – основной результат деятельности исследователя.
Максимальную ценность в среднем имеет публикация статьи в международном журнале с высоким импакт-фактором.
Для подготовки подобной публикации необходимо понимание методов оценки качества научного продукта.
Первичную оценку качества осуществляют рецензенты; рецензент – бесплатный помощник автора.
Вторичную оценку качества осуществляют пользователи (читатели), которые цитируют либо не цитируют научную публикацию.

Задачи лекции
Ознакомление со статистическим образом мышления.
Ознакомление с вероятностными суждениями.
Демонстрация критического анализа научной публикации.
Обучение способам интерпретации статистических выводов.

Поездка из дома на работу
Запереть дверь квартиры.
Спуститься на 1й этаж.
Дойти до остановки.
Дождаться транспорта.
Поездка в транспорте.
Дойти до здания университета.
Дойти от дверей до рабочего места.

Поездка из дома на работу
Запереть дверь квартиры. – 30 с.
Спуститься на 1й этаж. – 90 с.
Дойти до остановки. – 120 с.
Дождаться автобуса. – 600 с.
Поездка в автобусе. – 600 с.
Дойти до здания университета. – 120 с.
Дойти от дверей до рабочего места.–120с.
ВСЕГО 1680 с. (=28 мин.)

Поездка из дома на работу
Что представляет собой, с точки зрения математической статистики, полученная величина (1680 с.)?

Поездка из дома на работу
Что представляет собой, с точки зрения математической статистики, полученная величина (1680 с.)?
Это - среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины.

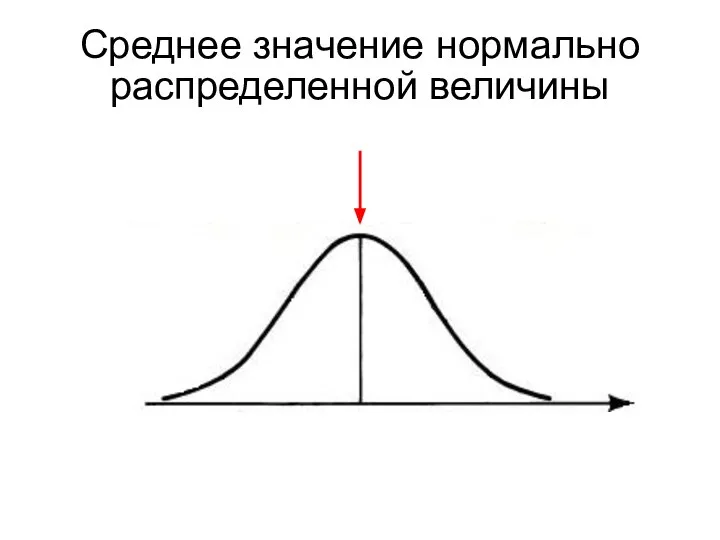
Среднее значение нормально распределенной величины

Поездка из дома на работу
Что представляет собой, с точки зрения математической статистики, полученная величина (1680 с.)?
Это - среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины.
Откуда взялась эта величина?

Поездка из дома на работу
Что представляет собой, с точки зрения математической статистики, полученная величина (1680 с.)?
Это - среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины.
Откуда взялась эта величина?
В результате неосознанного анализа множественных наблюдений.

Поездка из дома на работу
Что представляет собой, с точки зрения математической статистики, полученная величина (1680 с.)?
Это - среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины.
Означает ли это, что я гарантированно приду вовремя, если выйду из дома за 29 мин. до начала рабочего дня?

Поездка из дома на работу
Дождаться автобуса. – 600 с.
Доверительный интервал (CI95) 100-1100 с. (с вероятностью 95% я уложусь в это время).
Опоздание автобуса – дело обычное; но в конце концов он все-таки придет.
При расчете запаса времени это событие необходимо учитывать.
Для расчета запаса времени необходимо знать ответ на вопрос: «Какова цена опоздания на работу?».

Какова цена опоздания на работу?
Тюремное заключение.
Штраф в размере 5-дневной зарплаты.
Штраф в размере дневной зарплаты.
Шеф накричит.
Скорее всего, никто не заметит.

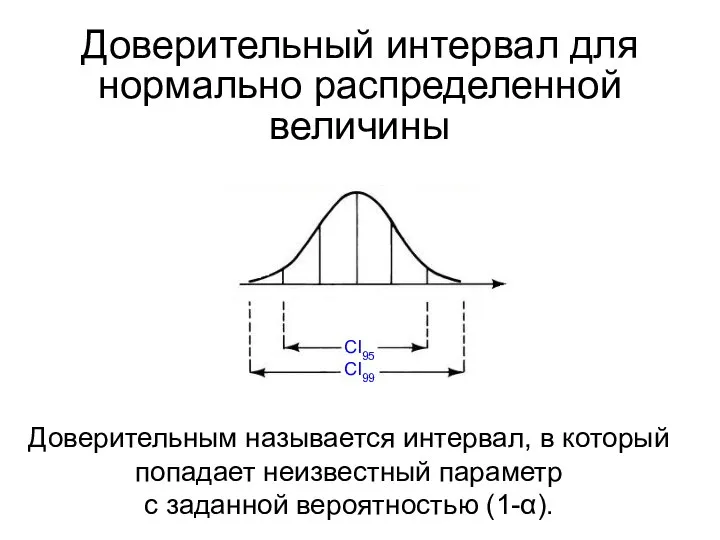
Доверительный интервал для нормально распределенной величины
Доверительным называется интервал, в который
попадает неизвестный параметр
с заданной вероятностью (1-α).
CI95
CI99

Какова цена опоздания на работу?
Какой принимаем доверительный интервал?*
Тюремное заключение. - CI99.99
Штраф в размере 5-дневной зарплаты.-CI99
Штраф в размере дневной зарплаты. - CI95
Шеф накричит. - CI90
Скорее всего, никто не заметит. – CI80
*Приведенные примеры доверительных интервалов не стоит
рассматривать как рекомендованные лектором.

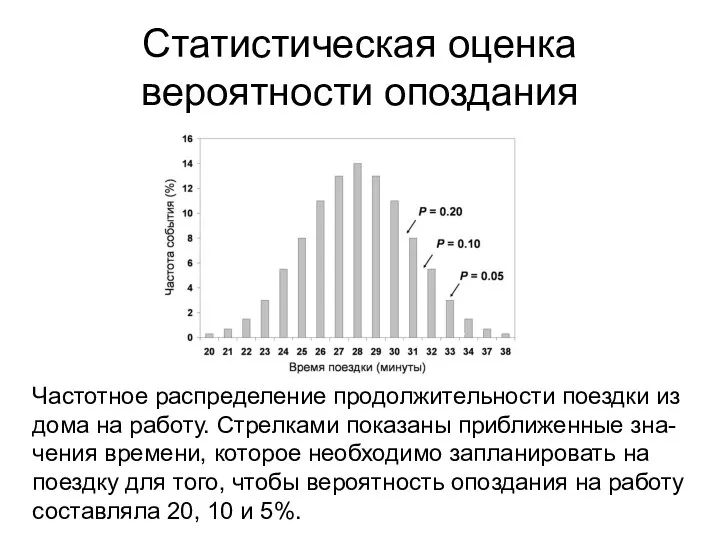
Статистическая оценка вероятности опоздания
Частотное распределение продолжительности поездки из
дома на работу. Стрелками показаны приближенные зна-
чения времени, которое необходимо запланировать на
поездку для того, чтобы вероятность опоздания на работу
составляла 20, 10 и 5%.

Статистическая природа «жизненного опыта»
Существенная часть «жизненного опыта» представляет собой результат неосознанной статистической обработки множественных наблюдений.
Мы используем теорию вероятностей гораздо чаще, чем сами об этом догадываемся.
Многие наши суждения носят вероятностный характер.

Примеры вероятностных высказываний
Команда А сильнее команды Б.
Овощи на колхозном рынке дешевле, чем в супермаркете.
Питбули агрессивнее пуделей.
Черемуха зацветает раньше рябины.
… … …

Примеры истинных высказываний
Площадь квадрата равна квадрату длины его стороны (функциональная связь).
Свинец тяжелее меди (фундаментальные свойства вещества).
Эйфелева башня выше главного здания Московского Государственного Университета (сравнение конечного количества однозначно определенных объектов).
Вчера в центре Архангельска шел снег (событие уже свершилось).

Биология / экология
Функциональные связи встречаются крайне редко.
Свойства объектов несводимы к фундаментальным свойствам вещества.
Ученые предпочитают делать выводы о неопределенном количестве объектов.
Ученые стараются делать выводы, имеющие предсказательную ценность.

Выводы
Биология – наука, основанная на вероятностных суждениях.
Следовательно, любое утверждение ученого должно сопровождаться оценкой вероятности того, что оно ложно (т.е. что из собранных материалов нужно было сделать иное заключение).

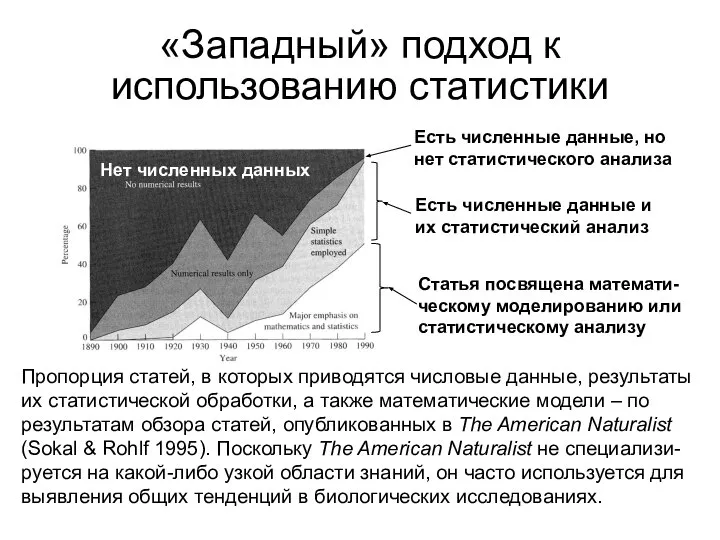
«Западный» подход к использованию статистики
Пропорция статей, в которых приводятся числовые данные, результаты
их статистической обработки, а также математические модели – по
результатам обзора статей, опубликованных в The American Naturalist
(Sokal & Rohlf 1995). Поскольку The American Naturalist не специализи-
руется на какой-либо узкой области знаний, он часто используется для
выявления общих тенденций в биологических исследованиях.
Нет численных данных
Статья посвящена математи-
ческому моделированию или
статистическому анализу
Есть численные данные, но
нет статистического анализа
Есть численные данные и
их статистический анализ

Частота встречаемости (%) статистических терминов (1990-1991)
>
>
>
>
≈
≈
>
>
<
Данные из: Будилова и др. (1995) Журн. Общ. Биол. Т. 56 № 2 с. 179-190

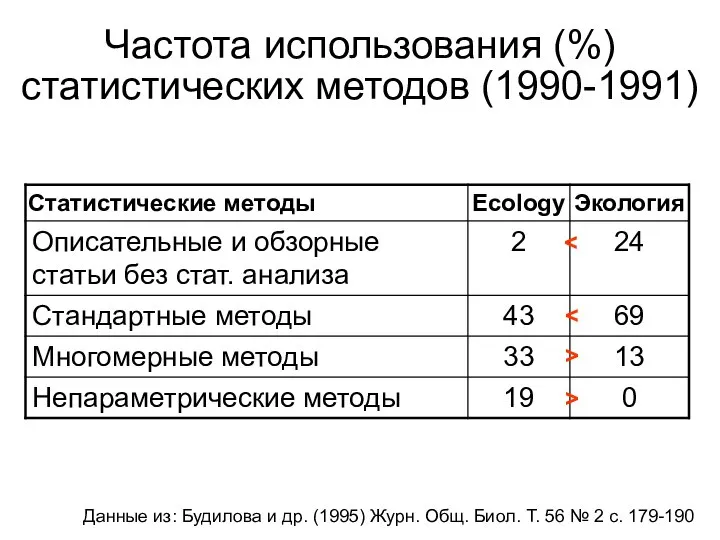
Частота использования (%) статистических методов (1990-1991)
<
>
>
<
Данные из: Будилова и др. (1995) Журн. Общ. Биол. Т. 56 № 2 с. 179-190

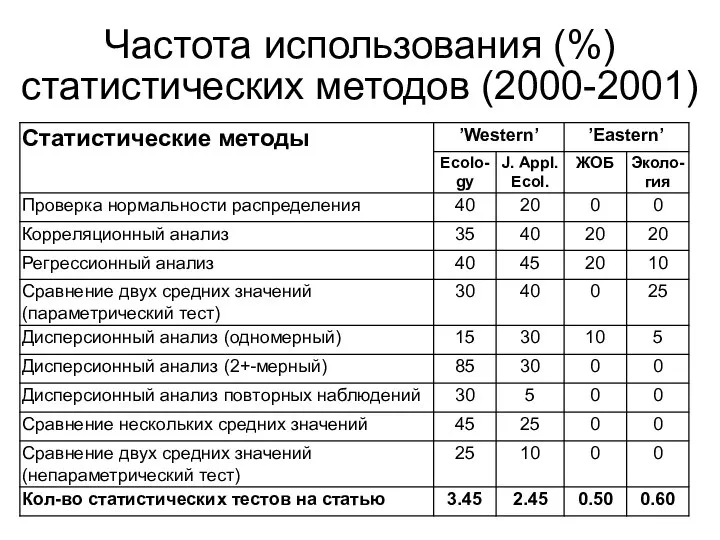
Частота использования (%) статистических методов (2000-2001)

Причины пренебрежения статистическим анализом
Практические:
Непонимание важности;
Неумение пользоваться;
Необязательность для публикации статьи;
Опасение за качество своих данных.
Теоретические:
Философы времен Т.Д. Лысенко;
Проф. В.С. Ипатов (СПбГУ).

Анализ статьи Ильина и Смирнова (2000) – Экология № 2, с. 118-124.
Каково методическое качество этого исследования?
Пригодны ли данные, приведенные авторами, для проверки выдвинутой ими гипотезы?
Согласуются ли выводы авторов с приведенными ими данными?

Анализ статьи Ильина и Смирнова (2000) – Экология № 2, с. 118-124.
Было ли спланировано это исследование?
Пригодны ли данные, приведенные авторами, для проверки выдвинутой ими гипотезы?
Согласуются ли выводы авторов с приведенными ими данными?

Анализ статьи Ильина и Смирнова (2000) – Экология № 2, с. 118-124.
Было ли спланировано это исследование? – Нет.
Пригодны ли данные, приведенные авторами, для проверки выдвинутой ими гипотезы?
Согласуются ли выводы авторов с приведенными ими данными? – Из статьи не ясно, но можно проверить.

Анализ статьи Ильина и Смирнова (2000) – Экология № 2, с. 118-124.
Было ли спланировано это исследование? – Нет.
Пригодны ли данные, приведенные авторами, для проверки выдвинутой ими гипотезы? – Нет.
Согласуются ли выводы авторов с приведенными ими данными? – Из статьи не ясно, но можно проверить.

Анализ статьи Ильина и Смирнова (2000) – Экология № 2, с. 118-124.
Было ли спланировано это исследование? – Нет.
Пригодны ли данные, приведенные авторами, для проверки выдвинутой ими гипотезы? – Нет.
Согласуются ли выводы авторов с приведенными ими данными? – Из статьи не ясно, но можно проверить.

Согласуются ли выводы Ильина и Смирнова (2000) с приведенными ими данными?
Гипотеза 1: связи с разными типами рельефа одинаковы в теплое и холодное время года;
Гипотеза 2: распространение видов не связано с рельефом (а – в теплое время года, б – в холодное время года).
В этом случае количество находок должно быть пропорционально площадям различных типов рельефа.
Определяем площади, занятые разными типами рельефа, и считаем количество находок на них.
Применяем простейший метод анализа (критерий Х2).

Согласуются ли выводы Ильина и Смирнова (2000) с приведенными ими данными?
Расчеты, выполненные лектором, показали: в целом – не согласуются!
15 из 30 утверждений авторов (в красных рамках) противоречат их собственным данным.

Анализ статьи Ильина и Смирнова (2000) – Экология № 2, с. 118-124.
Данные, собранные авторами, непригодны для проверки выдвинутой ими гипотезы. – Работа не была спланирована; основана на материалах, собранных для других целей!
Даже к том случае, если бы эти данные были пригодны для проверки этой гипотезы, половина сделанных авторами выводов противоречит их собственным данным. – Не было проведено статистического анализа данных!

Анализ статьи Ильина и Смирнова (2000) – Экология № 2, с. 118-124.
Данные, собранные авторами, непригодны для проверки выдвинутой ими гипотезы. – Работа не была спланирована; основана на материалах, собранных для других целей!
Даже к том случае, если бы эти данные были пригодны для проверки этой гипотезы, половина сделанных авторами выводов противоречит их собственным данным. – Не было проведено статистического анализа данных!

Старые НЕдобрые времена…
“…нас, биологов, не интересуют математические выкладки, подтверждающие практически бесполезные статистические формулы…”
“применение средств математики отводит нас, естествоиспытателей, от познания природы”
Цитировано по критической статье: Гнеденко Б.В.
О роли математических методов в биологических исследованиях // Вопросы философии. 1959.
№ 1. С. 85–97

Старые НЕдобрые времена…
Дополнительная информация:
Леонов В.П. Долгое прощание с лысенковщиной // Биометрика. 1999. URL: http://www.biometrica.tomsk.ru/lis.htm
Любищев А.А. Об ошибках в применении математики в биологии. I. Ошибки от недостатка осведомленности // Журн. общ. биол. 1969. Т. 30. № 5. С. 572–584.
Любищев А.А. Об ошибках в применении математики в биологии. 2. Ошибки, связанные с избытком энтузиазма // Журн. общ. биол. 1969. Т. 30. № 6, с. 715-723.

Современные противники статистического анализа
«применение вероятностной оценки оправдано только в тех случаях, когда исследуемые варьирующие признаки в выборке соответствуют нормальному случайному распределению или не слишком от него отличаются» (с. 1495)
Ипатов В.С. Осторожно – биометрика. (Об использовании оценок «достоверности» при исследовании количественных закономерностей // Бот. журн. 2010. Т. 95. № 10. С. 1494–1498.

Это полезно запомнить:
Существенная часть «жизненного опыта» представляет собой результат неосознанной статистической обработки множественных наблюдений.
В науке необходима бóльшая точность, чем в повседневной жизни.
Следовательно, любое утверждение ученого должно сопровождаться оценкой вероятности того, что оно ложно (т.е., что из собранных материалов нужно было сделать иное заключение).

Учимся понимать
статистические выводы
Пример 1
Газета Guardian, сообщая об участившихся случаях раковых заболеваний в городе Aldermaston (где находится производство расщепляющихся веществ): “probability of chance occurrence [вероятность случайного наблюдения] is 1 of 10,000,000”.
Вероятность того, что при случайном распределении раковых заболеваний по территории страны могла возникнуть наблюдаемая картина, составляет 1 : 10,000,000.

Учимся понимать
статистические выводы
Пример 1
Газета Guardian, сообщая об участившихся случаях раковых заболеваний в городе Aldermaston (где находится производство расщепляющихся веществ): “probability of chance occurrence [вероятность случайного наблюдения] is 1 of 10,000,000”.
Вероятность того, что при случайном распределении раковых заболеваний по территории страны могла возникнуть наблюдаемая картина, составляет 1 : 10,000,000.

Учимся понимать
статистические выводы
Какую именно гипотезу проверяли авторы?
Вариант 1
Нулевая гипотеза 1: случаи раковых заболеваний распределены по территории страны случайным образом.
Альтернативная гипотеза 1: случаи раковых заболеваний рас- пределены по территории страны НЕслучайным образом.
Вариант 2
Нулевая гипотеза 2: частота раковых заболеваний в городе Aldermaston не отличается от средней по стране.
Альтернативная гипотеза 2: частота раковых заболеваний в городе Aldermaston отличается от средней по стране.
Вариант 3
Нулевая гипотеза 3: частота раковых заболеваний в городе Aldermaston не отличается от средней по стране.
Альтернативная гипотеза 3: частота раковых заболеваний в городе Aldermaston выше, чем в среднем по стране.

Учимся понимать
статистические выводы
Все три варианта имеют право на существование.
Вариант 1 отличается от вариантов 2 и 3 методами как сбора, так и обработки данных.
Вариант 3 отличается от варианта 2 методом обработки данных.
Для решения задачи 3 требуется меньшая выборка, чем для решения задачи 2 с той же точностью.

Учимся понимать
статистические выводы
Из опубликованного вывода не ясно, какую именно гипотезу проверяли авторы исследования.
Эта гипотеза, несомненно, была упомянута в работе (просто газетчики про нее не написали).
От проверяемой гипотезы зависят способ сбора материала и объемы выборок.
Этим определяется необходимость тщательного планирования любого исследования, выводы которого будут носить вероятностный характер.

Учимся понимать
статистические выводы
Величина эффекта из опубликованного вывода не очевидна.
Для определения величины эффекта часто необходимо использовать иные методы, чем для определения его статистической значимости.
Величина эффекта часто важна для принятия решений (сравним, например, возрастание частоты раковых заболеваний на 1% и на 10%).

Учимся понимать
статистические выводы
Пример 2
«Размеры листа березы уменьшаются с широтой места сбора (r = -0.76, n = 10, P = 0.01).»
Вероятность того, что на самом деле в генеральной совокупности изучаемые признаки не связаны друг с другом (r = 0.00), составляет 1% (один случай из 100).

Учимся понимать
статистические выводы
Пример 2
«Размеры листа березы уменьшаются с широтой места сбора (r = -0.76, n = 10, P = 0.01).»
Вероятность того, что на самом деле в генеральной совокупности изучаемые признаки не связаны друг с другом (r = 0.00), составляет 1% (один случай из 100).

Учимся понимать
статистические выводы
Пример 2
«Размеры листа березы уменьшаются с широтой места сбора (r = -0.76, n = 10, P = 0.01).»
Вероятность того, что на самом деле в генеральной совокупности изучаемые признаки не связаны друг с другом (r = 0.00), составляет 1% (один случай из 100).
Достигнутый уровень значимости –
это вероятность получения такого же
(или более экстремального) значения
коэффициента корреляции в выборке из
генеральной совокупности, в которой
отсутствует корреляция между
изучаемыми признаками.

Учимся понимать
статистические выводы
Пример 2
«Размеры листа березы уменьшаются с широтой места сбора (r = -0.76, n = 10, P = 0.01).»
Вероятность того, что на самом деле в генеральной совокупности изучаемые признаки не скоррелированы друг с другом (r = 0.00), составляет 1% (один случай из 100).

Учимся понимать
статистические выводы
Пример 3
«Размеры листа березы не зависят от широты места сбора (r = -0.36, n = 10, P = 0.31).»
Вероятность того, что на самом деле в генеральной совокупности изучаемые признаки не связаны друг с другом (r = 0.00), составляет 1% (один случай из трех).

Учимся понимать
статистические выводы
Пример 3
«Размеры листа березы не зависят от широты места сбора (r = -0.36, n = 10, P = 0.31).»
Вероятность того, что на самом деле в генеральной совокупности изучаемые признаки не скоррелированы друг с другом (r = 0.00), составляет 31% (один случай из трех).

Учимся понимать
статистические выводы
В чем разница между примерами 2 и 3?
«Размеры листа березы уменьшаются с широтой места сбора (r = -0.76, n = 10, P = 0.01).»
«Размеры листа березы не зависят от широты места сбора (r = -0.36, n = 10, P = 0.31).»
Проверяли одну и ту же гипотезу.
Использовали однотипный материал.
Пришли к принципиально разным выводам (по бинарной шкале: да/нет).

Учимся понимать
статистические выводы
В чем разница между примерами 2 и 3?
«Размеры листа березы уменьшаются с широтой места сбора (r = -0.76, n = 10, P = 0.01).»
«Размеры листа березы не зависят от широты места сбора (r = -0.36, n = 10, P = 0.31).»
Проверяли одну и ту же гипотезу.
Использовали однотипный материал.
Пришли к принципиально разным выводам (по бинарной шкале: да/нет).

Учимся понимать
статистические выводы
Принципиальной разницы между примерами 2 и 3 нет!
Проверяли одну и ту же гипотезу.
Использовали однотипный материал.
Получили разную оценку вероятности того, что нулевая гипотеза (отсутствие корреляции) верна – 1% и 31%.
Договорились считать, что отклоняем нулевую гипотезу, если вероятность того, что она верна, не превышает 5%.

Практическая рекомендация
Не следует абсолютизировать «граничное» значение Р = 0.05 – это лишь условная граница между скорее всего верными и скорее всего ошибочными гипотезами.
Избегайте крайностей типа: «Значимые различия были найдены между популяциями А и В (Р = 0.045), в то время как популяции В и С не различались (Р = 0.055)» (пример реальный, приведен по: Yoccoz 1991).

Практическая рекомендация
Всегда приводите полученные значения вероятностей! Читатель вправе знать, насколько обоснован Ваш вывод:
«Значимые различия были найдены между популяциями А и В, в то время как популяции В и С не различались» - плохо!
«Значимые различия были найдены между популяциями А и В (Р = 0.045), в то время как популяции В и С не различались (Р = 0.055)» - хорошо!

Учимся понимать
статистические выводы
В примерах 2 и 3 получены разные оценки силы связи (-0.76 и -0.36) между размерами листа и широтой местности.
Однако с точки зрения проверяемой гипотезы (связь отсутствует / имеется) эти различия не представляют интереса.
С точки зрения здравого смысла эти различия представляют несомненный интерес.
Мы можем проверить гипотезу, что r1 = r2, но для этого потребуется другой метод анализа данных.

Величина эффекта и его статистическая значимость
Величина эффекта часто гораздо важнее его статистической значимости – как для принятий решений, так и для оценки важности полученного результата.
Сравним, например, сообщения о том, что в некоем городе частота раковых заболеваний за последние 10 лет возросла
на 10% при значимости 95.0%
на 0.1% при значимости 99.9%.
Очевидно, что первое сообщение встревожит жителей гораздо больше, хотя вероятность ошибочного вывода ниже во втором случае.
на 10% при значимости 95.0%
на 0.1% при значимости 99.9%.

Что значит «достоверно»?
Четкость формулировок чрезвычайно важна при описании как методики исследований, так и полученных результатов. Особенно важно стремиться к максимальному сужению смыслового спектра научных терминов.
В этом отношении описанию результатов статистического анализа явно «не повезло» в русскоязычной биологической и медицинской литературе, где прочно закрепилось слово «достоверность» (Зорин, 2000, 2011).

http://www.hta-rus.ru/files/s15_1352793575.pdf

Авторы отечественных медицинских статей достаточно произвольно употребляют статистическую терминологию наравне с обыденными значениями тех же слов, их однокоренными аналогами и синонимами.
Слова «достоверность» и «значимость» как употребляли в 1997 – 1998 гг., так и продолжают употреблять в 2018 г. как взаимозаменяемые, нередко в одном и том же тексте, наделяя их функцией термина, и по-прежнему используют наряду с терминами и как обыденные слова.

Что значит «достоверно»?

Что значит «достоверно»?
«Вероятность случайности различий соответствует достоверности».
(Пример реальный. Я так и не смог понять, оказались анализируемые различия значимыми или не значимыми.)
«Смутно пишут о том, о чем смутно представляют.»
М. В. Ломоносов

Что значит «достоверно»?
«Вероятность случайности различий соответствует достоверности».
(Пример реальный. Я так и не смог понять, оказались анализируемые различия значимыми или не значимыми.)
«Смутно пишут о том, о чем смутно представляют.»
М. В. Ломоносов

Что значит «достоверно»?
«Вероятность случайности различий соответствует достоверности».
(Пример реальный. Я так и не смог понять, оказались анализируемые различия значимыми или не значимыми.)
«Смутно пишут о том, о чем смутно представляют.»
М. В. Ломоносов

Что значит «достоверно»?
Изначально использование понятия «достоверность» было связано с некорректным переводом термина «significance».
Определенную роль в его широком распространении сыграла ошибочная ассоциация с одним из понятий теории вероятности – достоверным событием (событие, вероятность которого строго равна единице).

Что значит «достоверно»?
В любом случае, поскольку слово «достоверность» перегружено смыслом, в строго статистическом значении его лучше не употреблять, а использовать термин «статистическая значимость».
Прежде всего, это следует делать из-за того, что «достоверность» подсознательно ассоциируется с «абсолютной доказанностью», «надежностью», «несомненностью», «безошибочностью», а «достоверная связь» – с причинно-следственной, что некорректно по отношению к вероятностным выводам.

Что значит «достоверно»?
Статистика не занимается «определением достоверности» – статистический анализ позволяет лишь определить вероятность того, что некоторая гипотеза верна.

Что может статистика?
Выполнить свертку информации: подсчет некоторых характеристик выборки и (на основании этого) вынесение вероятностных суждений о характеристиках исследуемой популяции.
Пример: С вероятностью 0.95 средняя длина крыла комнатной мухи, пойманной в г. Мончегорске попадает в интервал от 5.73 до 6.28 мм.
Выполнить проверку гипотезы, то есть вынести вероятностное суждение по поводу истинности либо ложности некоего априорно сформулированного утверждения.
Пример: Вероятность того, что средняя длина крыла комнатной мухи в исследуемой выборке из г. Мончегорска отличается от средней длины крыла комнатной мухи в исследуемой выборке из г. Апатиты исключительно вследствие воздействия на эти выборки случайных факторов равна 0.8% (то есть Р = 0.008).
Провести статистическое моделирование.

Статистика не может:
Определить генеральную совокупность, которую Вы хотите изучить.
Взять репрезентативную выборку из этой генеральной совокупности.
Случайным образом распределить повторности по отношению к планируемым экспериментальным воздействиям.
Выбрать переменные для измерения / подсчета.
Выбрать способ измерения / учета, не приводящий к получению смещенной оценки.
Эти задачи решаются во время планирования
исследования (эксперимента).

Это полезно запомнить…
Отказ от использования статистического анализа может привести к ошибочной интерпретации данных и стать причиной заблуждений.
Отказ от использования статистического анализа (там, где он необходим) приведет к отклонению рукописи практически любым международным журналом.
Достигнутый уровень значимости – это вероятность получения такого же (или более экстремального) значения критерия в длинной серии повторных выборок при условии справедливости нулевой гипотезы.