Содержание
- 2. Содержание: 1. Коэффициенты квадратного уравнения теория задачи 2. Полные и неполные квадратные уравнения теория задачи 3.
- 3. Квадратное уравнение: ax2 + bx + c = 0, a ≠ 0 а – первый (старший)
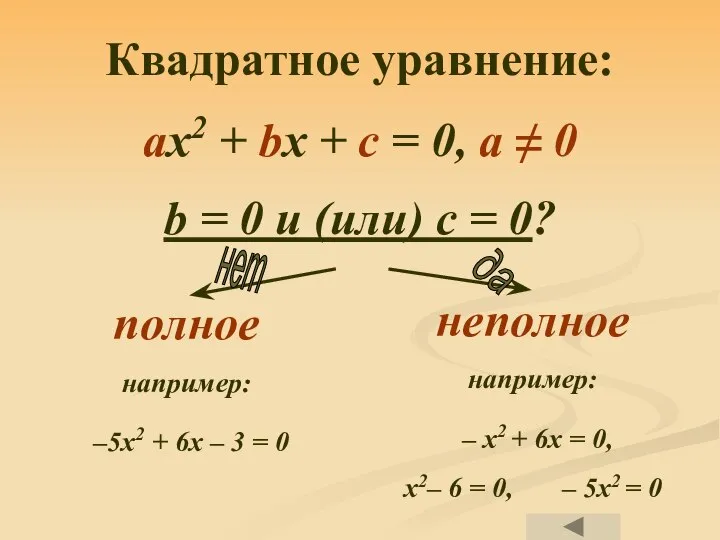
- 4. Квадратное уравнение: ax2 + bx + c = 0, a ≠ 0 b = 0 и
- 5. Квадратное уравнение: ax2 + bx + c = 0, a ≠ 0 Формула корней квадратного уравнения:
- 6. Исследование существования корней квадратного уравнения: ax2 + bx + c = 0, a ≠ 0 Если
- 7. Если а + b + с = 0, то уравнение имеет 2 корня: x = 1
- 8. Квадратное уравнение: ax2 + bx + c = 0, a ≠ 0 а = 1? уравнение
- 9. x2 + px + q = 0 – приведенное квадратное уравнение Теорема Виета прямая Если х1
- 10. Формулы Виета где р и q – коэффициенты приведенного квадратного уравнения х2 + рх + q
- 11. 1) 7х2 + 3х + 5 = 0; 2) х2 – 2х + 3,2 = 0;
- 12. Какие из данных квадратных уравнений являются неполными? 1) 7х2 + 3х + 5 = 0; 2)
- 13. Выясните, имеет ли заданное уравнение корни. В случае утвердительного ответа, укажите их количество. b2 – 4ac
- 14. Какие из данных квадратных уравнений являются приведенными? 1) 7х2 + 3х + 5 = 0; 2)
- 15. Выясните, имеют ли данные уравнения корни. В случае утвердительного ответа найдите их, используя формулы Виета. а
- 17. Скачать презентацию













 Задания на развитие логики
Задания на развитие логики Тригонометрические уравнения, приводимые к квадратным
Тригонометрические уравнения, приводимые к квадратным Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Системы линейных алгебраических уравнений. Лекция 1
Системы линейных алгебраических уравнений. Лекция 1 Треугольники
Треугольники Куб. Параллелепипед. Тест
Куб. Параллелепипед. Тест Удивительная симметрия
Удивительная симметрия Сравнение чисел. 1 класс
Сравнение чисел. 1 класс В мире математики
В мире математики Пересекающиеся прямые
Пересекающиеся прямые Кенгуру – математика для всех
Кенгуру – математика для всех Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Парная регрессия и корреляция
Парная регрессия и корреляция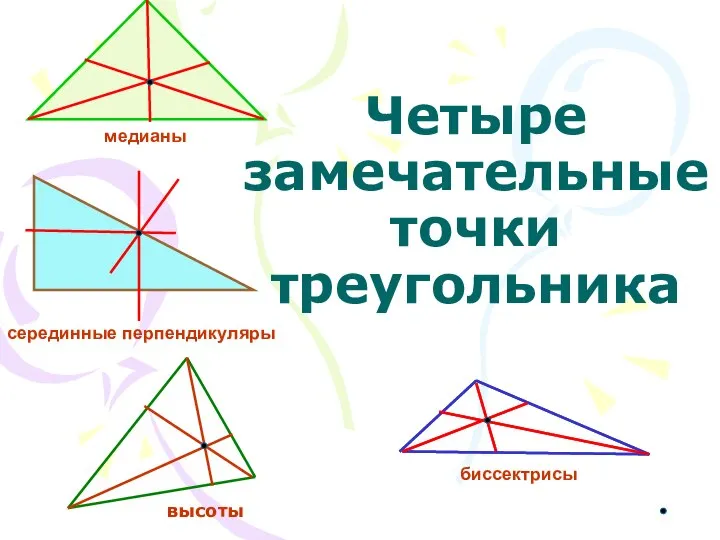 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Математика. Раздел 6. Метод координат в пространстве. Занятие 66. Уравнение плоскости
Математика. Раздел 6. Метод координат в пространстве. Занятие 66. Уравнение плоскости Перестановки. Размещения
Перестановки. Размещения Вычисление определителя третьего порядка по правилу треугольников
Вычисление определителя третьего порядка по правилу треугольников Эконометрика. Семинар 2. Решение задачи 4
Эконометрика. Семинар 2. Решение задачи 4 Множества
Множества Дроби
Дроби Первые единицы измерения длины. 1 класс
Первые единицы измерения длины. 1 класс Algebraic constructions generated by causal structure of space-times
Algebraic constructions generated by causal structure of space-times Пивкин ИКС-34 (2)
Пивкин ИКС-34 (2) Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Загадки и тайны треугольника
Загадки и тайны треугольника Аксиомы стереометрии
Аксиомы стереометрии Разложение определителя. Нахождение обратной матрицы
Разложение определителя. Нахождение обратной матрицы