Векторы на плоскости

План.
1.Историческая справка.
2.Определение вектора.
3.Нулевой вектор.
4.Длина вектора.
5.Коллинеарные векторы.
6.Виды коллинеарных векторов.
7.Противоположные векторы.
8.Равные векторы.
9.Откладывание вектора от данной точки.

Историческая справка
Термин вектор (от лат. Vector – “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем.

Что такое вектор?
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением: например, скорость, сила, давление. Такие величины называются векторными величинами или векторами.

Геометрическое понятие вектора
ОПР: Отрезок, для которого указано , какой из его концов считается началом , а какой – концом, называется направленным отрезком или вектором.

Геометрическое понятие вектора
Направление вектора указывается стрелкой. Точка A называется началом вектора, а точка B – концом.
Векторы обозначаются латинскими буквами a, b, c, …, а также AB, CD, … (на первом месте ставится начало вектора).
В
А
Начало вектора
Конец вектора
C
D
a
b
c

Нулевой вектор
Любую точку плоскости можно считать вектором. Такой вектор называется нулевым.
Начало нулевого вектора совпадает с его концом.
Нулевой вектор обозначается 0 или СС.
М
С

Длина (модуль) вектора.
ОПР: Расстояние между началом и концом вектора называется длиной или модулем вектора.
Обозначение: |а| или |АВ|.
Длина нулевого вектора равна нулю.
|0| =0

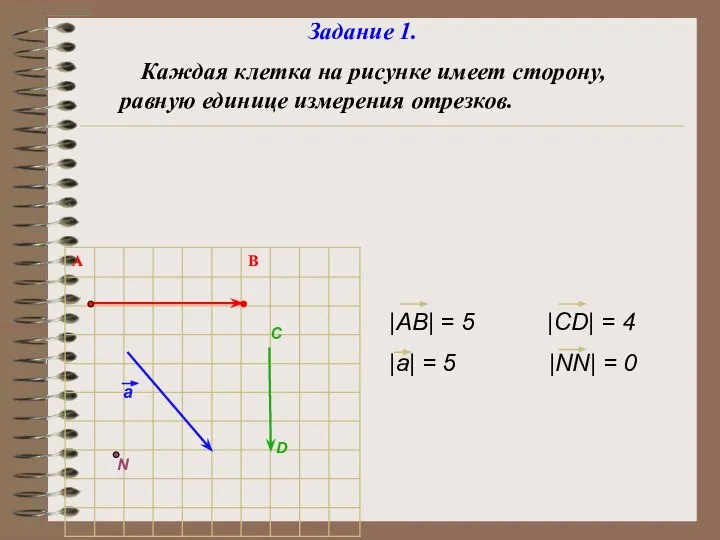
Каждая клетка на рисунке имеет сторону, равную единице измерения отрезков.
a
C
D
N
|AB| = 5 |CD| = 4
|a| = 5 |NN| = 0
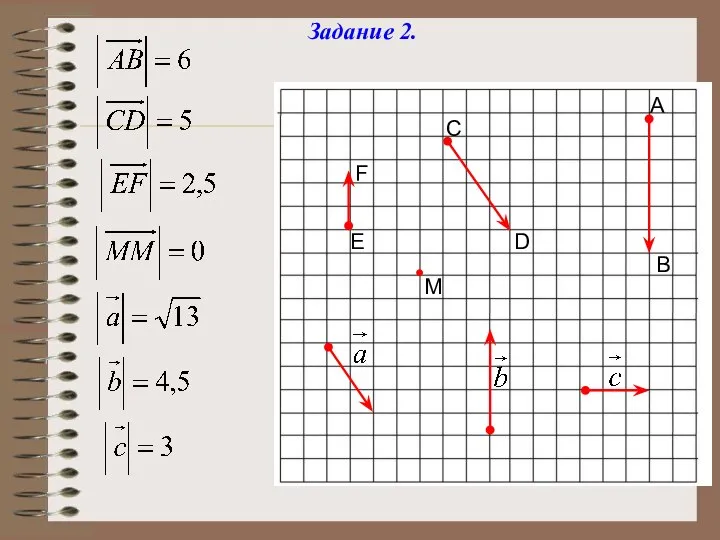
Задание 1.

Задание 2.
А
B
C
D
E
F
M

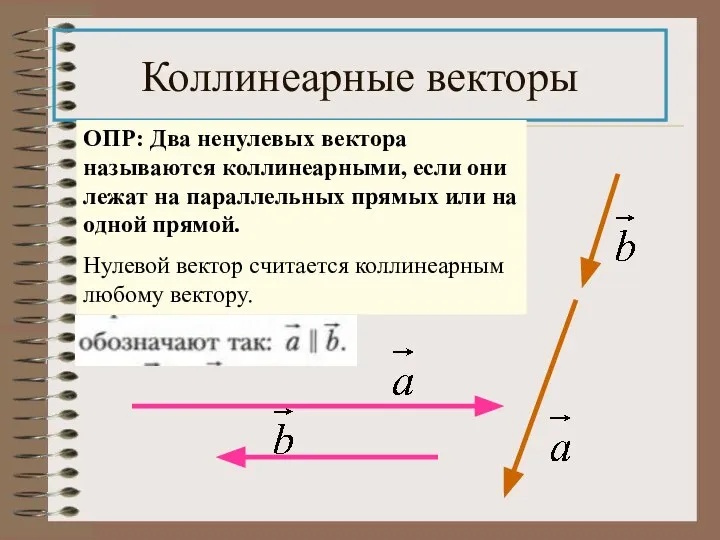
Коллинеарные векторы
ОПР: Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Нулевой вектор считается коллинеарным любому вектору.

Задание: укажите коллинеарные векторы
CD, KF, O, a, b – коллинеарные
O, a – коллинеарные
O, NP – коллинеарные
NP, m – не коллинеарные

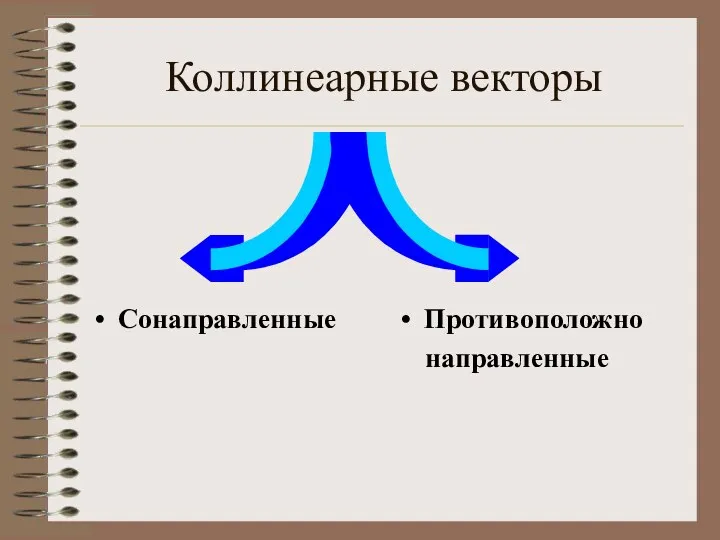
Коллинеарные векторы
Сонаправленные
Противоположно
направленные

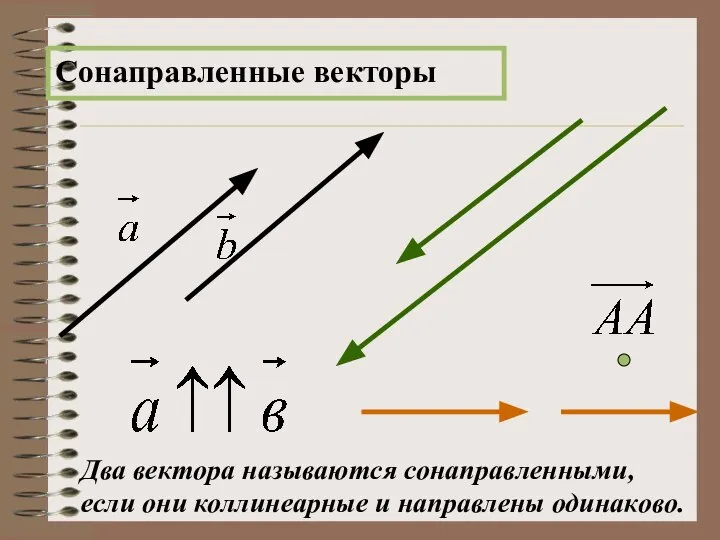
Сонаправленные векторы
Два вектора называются сонаправленными,
если они коллинеарные и направлены одинаково.

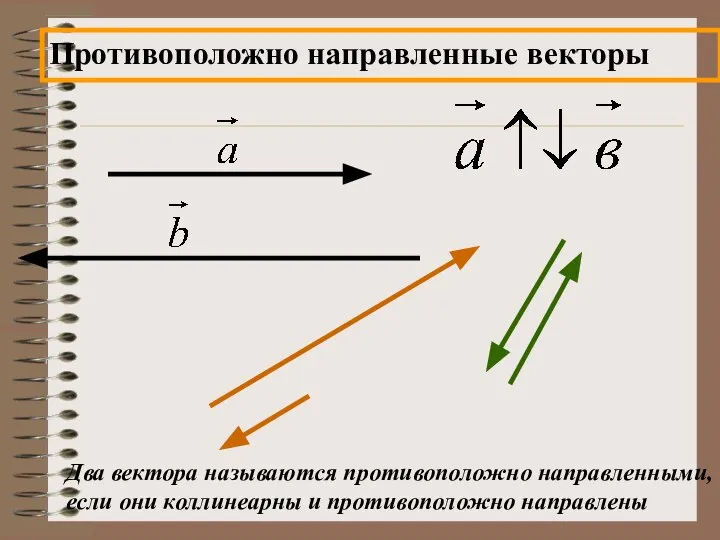
Противоположно направленные векторы
Два вектора называются противоположно направленными,
если они коллинеарны и противоположно направлены

Свойства коллинеарных векторов.

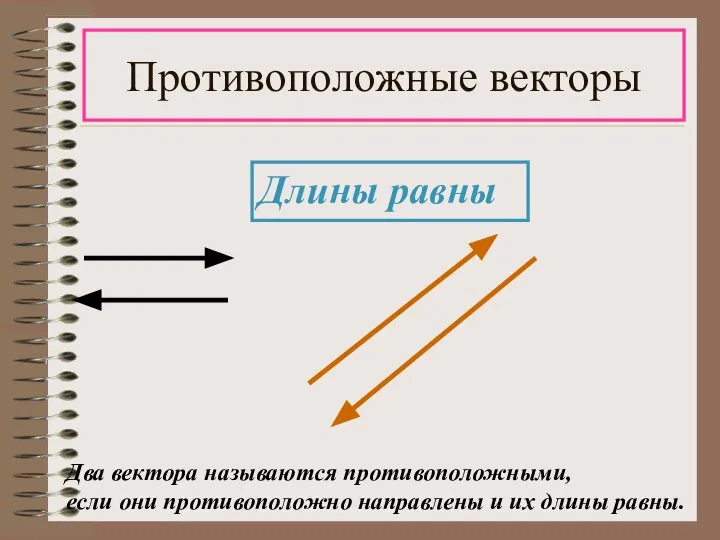
Противоположные векторы
Длины равны
Два вектора называются противоположными,
если они противоположно направлены и их длины равны.

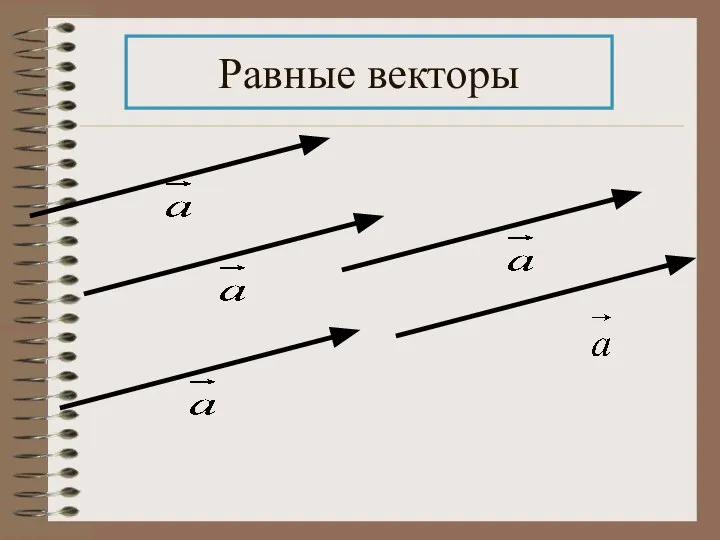
Равные векторы

ОПР: Ненулевые векторы называются равными, если они сонаправлены и их модули равны. Все нулевые векторы равны друг другу.
Свойство равных векторов.

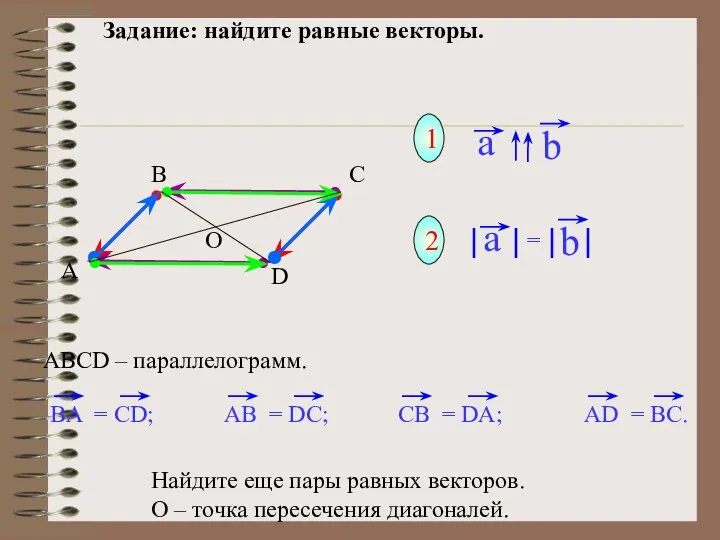
Задание: найдите равные векторы.
1
2
Найдите еще пары равных векторов.
О – точка пересечения диагоналей.

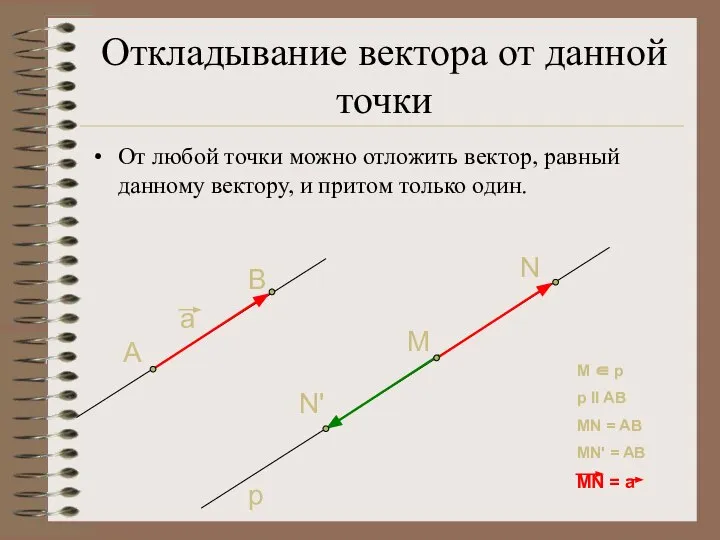
Откладывание вектора от данной точки
От любой точки можно отложить вектор, равный данному вектору, и притом только один.
а
А
В
М
N'
N
p
M ∈ p
p II AB
MN = AB
MN' = AB
MN = a

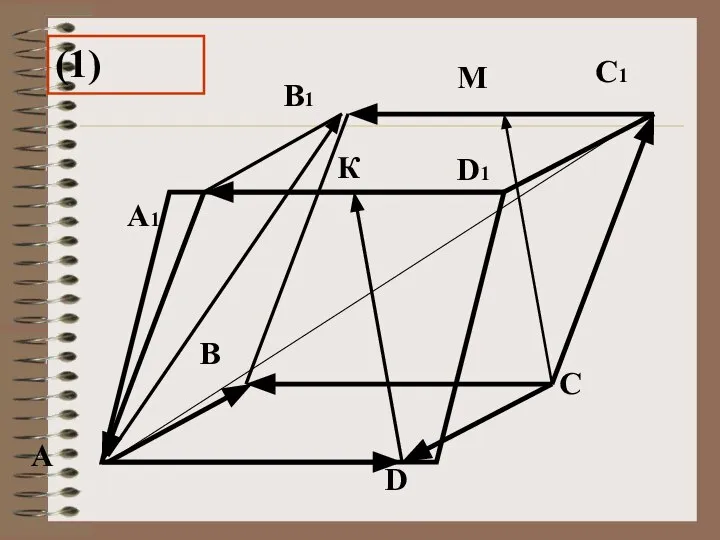
Упражнение
На рисунке 1 изображён параллелепипед ABCDA1B1C1D1.
Точки М и К – середины рёбер В1С1 и А1D1. Укажите все пары:
А) сонаправленных векторов
Б) противоположно направленных векторов
В) равных векторов.

В
С
D
А
D1
С1
В1
А1
М
К
(1)

Ответы.
А)KD и MC ,BC и B1C1 , A1D1 и BC , A1D1 и B1C1.
Б)DC и AB , AD и BC , AD и B1C1 ,
AD и A1D1.
В)DK и MC , AB и CD , AB1 и AC , B1C1 и BC ,
AD и B1C1.

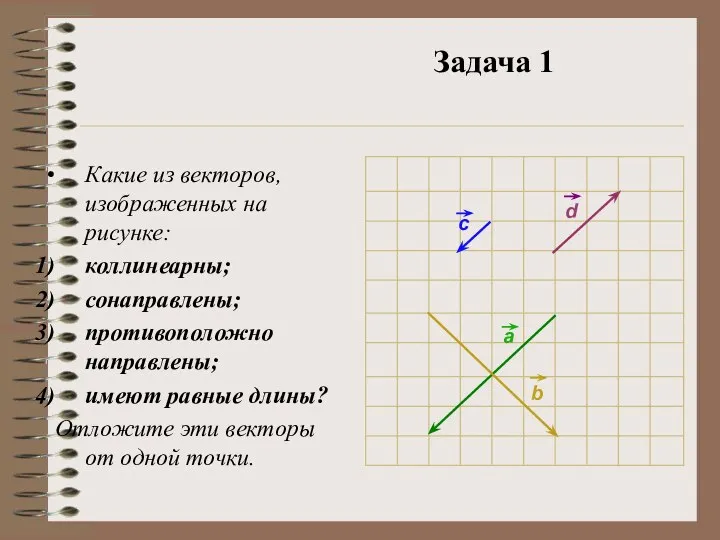
Задача 1
Какие из векторов, изображенных на рисунке:
коллинеарны;
сонаправлены;
противоположно направлены;
имеют равные длины? Отложите эти векторы от одной точки.
a
b
d
c

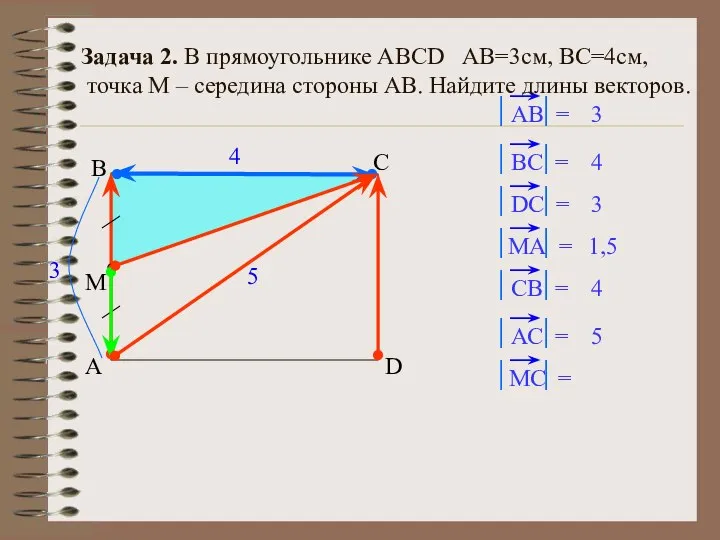
С
А
В
D
4
3
4
3
1,5
4
5
5
M
Задача 2. В прямоугольнике АВСD АВ=3см, ВС=4см,
точка М – середина стороны АВ. Найдите длины векторов.

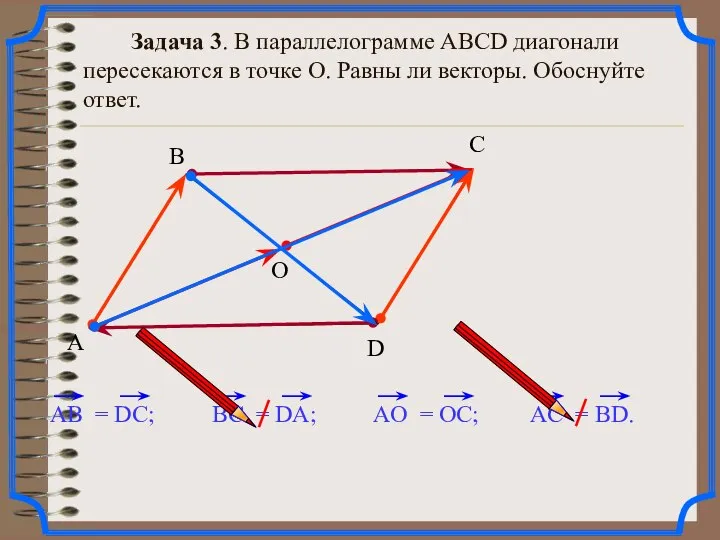
Задача 3. В параллелограмме АВСD диагонали пересекаются в точке О. Равны ли векторы. Обоснуйте ответ.
А
В
С
D