Содержание
- 2. Область определения булевой функции конечна -> можно задать значения во всех точках (таблица истинности)
- 3. Наиболее важные функции Отрицание Конъюнкция Дизъюнкция Импликация Эквиваленция (или эквивалентность)
- 4. Отрицание
- 5. Конъюнкция
- 6. Дизъюнкция
- 7. Импликация
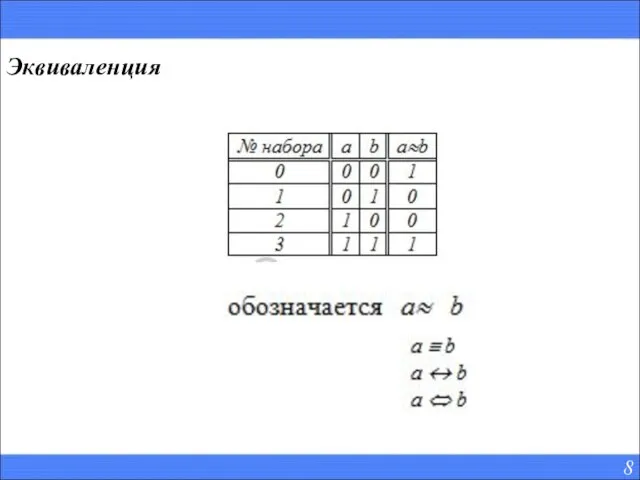
- 8. Эквиваленция
- 9. Способы задания булевых функций Задание булевой функции таблицей истинности
- 10. Задание булевой функции вектором значений f(0,0,...,0,0), f(0,0,...,0,1), f(0,0,...,1,0), f(0,0,...,1,1),..., f(1,1,...,0,0), f(1,1,...,0,1), f(1,1,...,1,0), f(1,1,...,1,1) φf=00010111
- 11. Задание булевой функции номером Каждой функции присваивается порядковый номер в виде натурального числа, двоичный код которого
- 12. Пример Найти порядковый номер функции f(x,y), принимающей следующие значения: f(0,0)=1, f(0,1)=1, f(1,0)=0, f(1,1)=1. Двоичный код, соответствующий
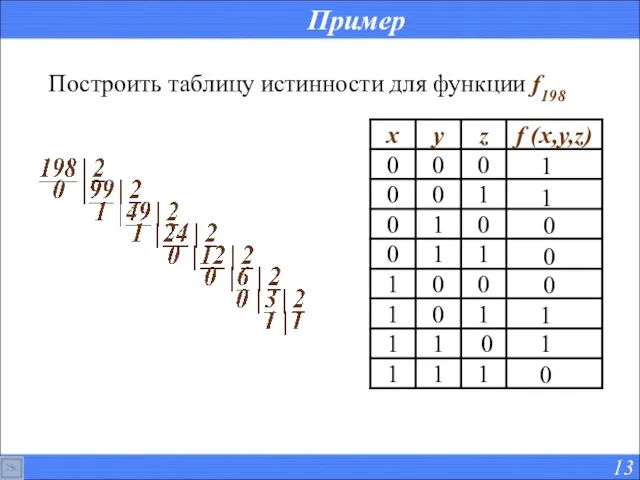
- 13. Пример Построить таблицу истинности для функции f198 0 0 0 0 1 1 1 1
- 14. Формулами
- 15. Приоритет выполнения операций Если в формуле отсутствуют скобки, то операции выполняются в следующей последовательности: Отрицание. Конъюнкция.
- 16. Формула называется выполнимой (опровержимой), если существует такой набор значений переменных, при которых эта формула принимает значение
- 17. Пусть А и В – две формулы, зависящие от одного и того же списка переменных. Будем
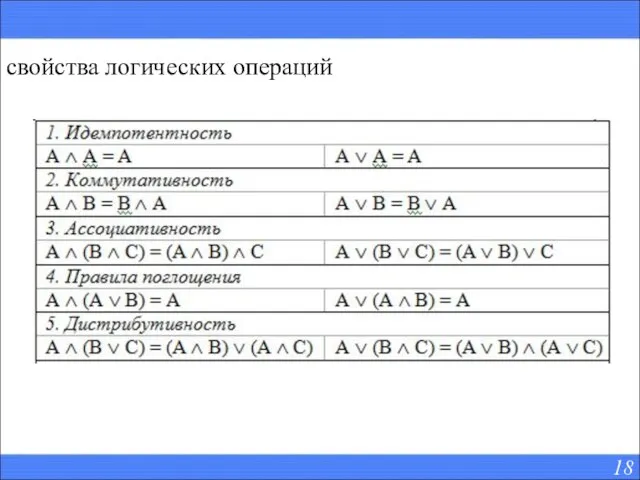
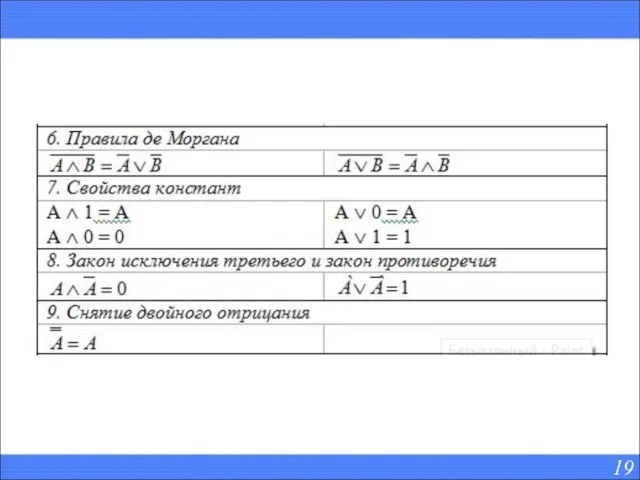
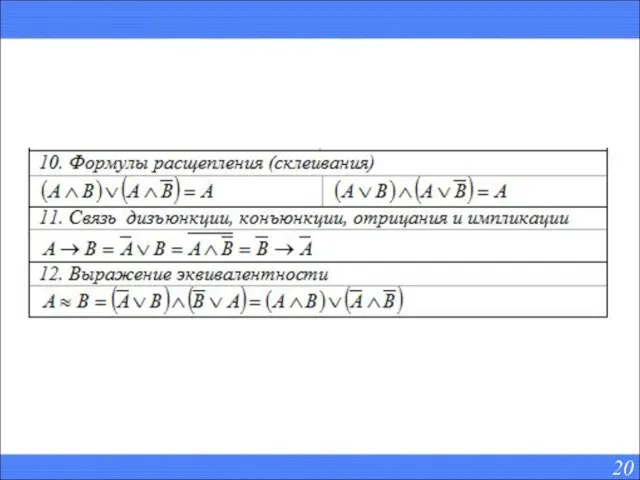
- 18. свойства логических операций
- 21. Любая из равносильностей легко может быть доказана с помощью таблицы истинности
- 23. Однако часто равносильность экономнее доказывать без составления полной таблицы истинности, а с помощью приведенных равносильностей Доказать
- 26. Нормальные формы Элементарной конъюнкцией называется конъюнкция, составленная из попарно различных переменных или отрицаний переменных. Дизъюнктивной нормальной
- 27. Элементарной дизъюнкцией называется дизъюнкция, составленная из попарно различных переменных или отрицаний переменных. Конъюнктивной нормальной формой (КНФ)
- 28. Совершенные нормальные формы Cовершенной ДНФ называется ДНФ, в которой - нет одинаковых элементарных конъюнкций и все
- 29. Совершенные нормальные формы Cовершенной КНФ называется КНФ, в которой - нет одинаковых элементарных дизъюнкций и -
- 30. Алгоритм получения СДНФ по таблице истинности Отметить те строки ТИ, в последнем столбце которых стоят 1:
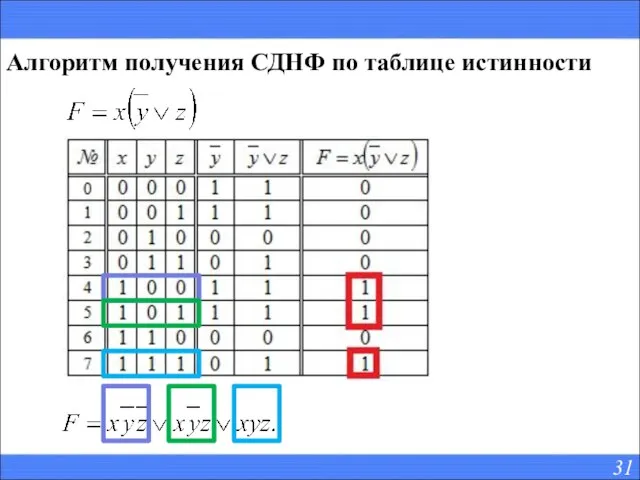
- 31. Алгоритм получения СДНФ по таблице истинности
- 32. Алгоритм получения СКНФ по таблице истинности Отметить те строки ТИ, в последнем столбце которых стоят 0:
- 33. Алгоритм получения СКНФ по таблице истинности
- 35. Скачать презентацию


























 Задачи на построение
Задачи на построение Магические цифры
Магические цифры Степенная функция и её график
Степенная функция и её график Производная
Производная Логика действий
Логика действий Работа с числами
Работа с числами Презентация на тему Логарифмическая функция, ее свойства и график
Презентация на тему Логарифмическая функция, ее свойства и график  Комбинаторика. Комбинаторные объекты
Комбинаторика. Комбинаторные объекты Лекция 5. Плоские и планарные графы
Лекция 5. Плоские и планарные графы Презентация по математике "Устные приемы вычисления и нумерация многозначных чисел" -
Презентация по математике "Устные приемы вычисления и нумерация многозначных чисел" - 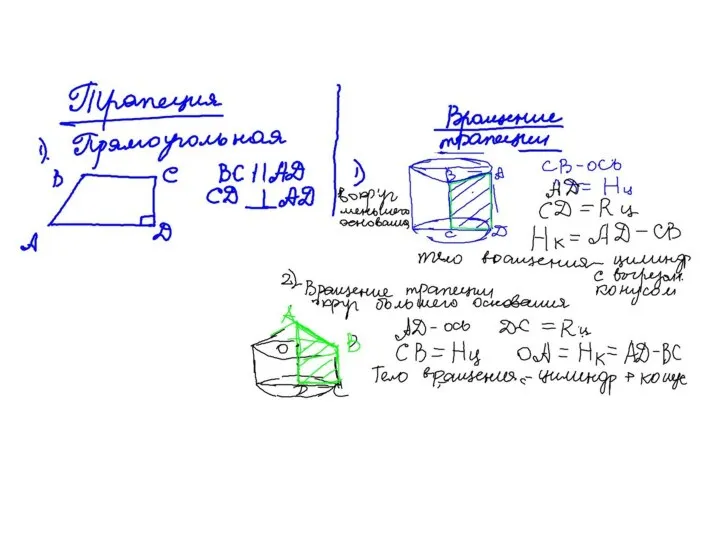 Вращение трапеции
Вращение трапеции Теорема Пифагора
Теорема Пифагора Косинус острого угла прямоугольного треугольника. 8 класс
Косинус острого угла прямоугольного треугольника. 8 класс Формулы логики
Формулы логики Окружность. Комбинации с окружностью. ЕГЭ
Окружность. Комбинации с окружностью. ЕГЭ История развития геометрии как науки
История развития геометрии как науки Матрицы и действия над ними
Матрицы и действия над ними Презентация на тему Факториал 9 класс
Презентация на тему Факториал 9 класс  Параллельность прямой и плоскости
Параллельность прямой и плоскости Повторение. Математика, 1 класс
Повторение. Математика, 1 класс Призма. Площади поверхностей. Объем призмы
Призма. Площади поверхностей. Объем призмы Умножение дробей
Умножение дробей Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ
Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ  חילוק מספרים מכוונים- למידה עצמאית
חילוק מספרים מכוונים- למידה עצמאית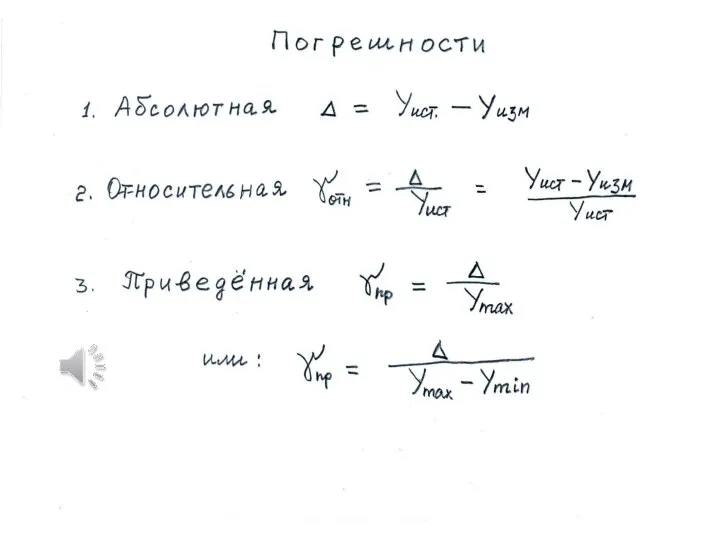 Погрешности. Погрешности измерений
Погрешности. Погрешности измерений Способы извлечения квадратного корня из многозначных чисел
Способы извлечения квадратного корня из многозначных чисел Теория вероятностей. Равновероятные возможности
Теория вероятностей. Равновероятные возможности Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений