Содержание
- 8. Решение
- 12. Матрица А - вырождена, то есть А = detA = 0. Тогда ее ранг r(А) =
- 13. Пусть базисный минор матрицы А, порядок которого равен r,находится в левом верхнем углу. В этом случае
- 14. Перепишем систему, оставив слева только r слагаемых в каждом уравнении: x1 , x2, …, xr -
- 16. Скачать презентацию













 математика дз
математика дз Делители и кратные
Делители и кратные Предметы геометрической формы. Логические задания
Предметы геометрической формы. Логические задания Первый признак равенства треугольников. Теорема
Первый признак равенства треугольников. Теорема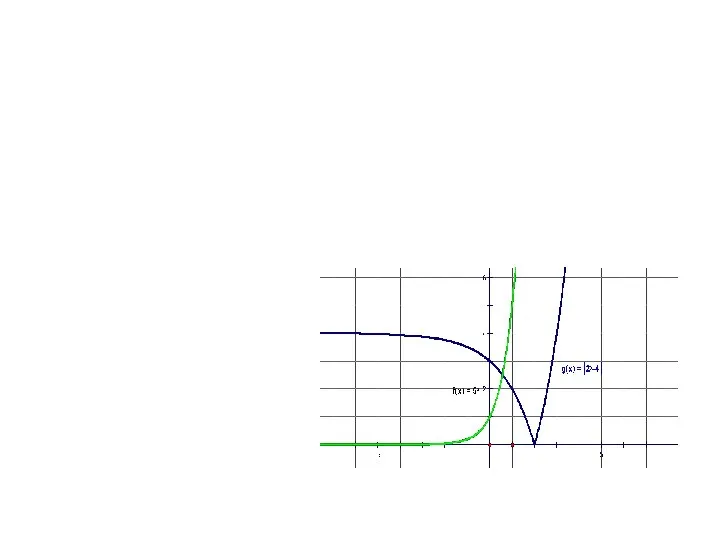 Показательные уравнения
Показательные уравнения Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата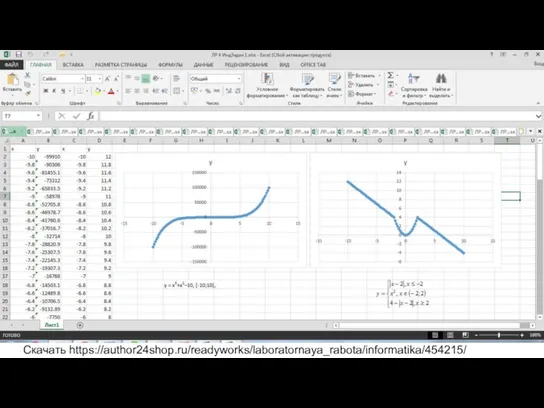 Постройте графики функций
Постройте графики функций Серединный перпендикуляр
Серединный перпендикуляр Решение задач на применение признаков равенства треугольников. 7 класс
Решение задач на применение признаков равенства треугольников. 7 класс Криволинейные интегралы (Лекция 6)
Криволинейные интегралы (Лекция 6) Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Презентация на тему Умножение и деление степеней
Презентация на тему Умножение и деление степеней  Измерение углов
Измерение углов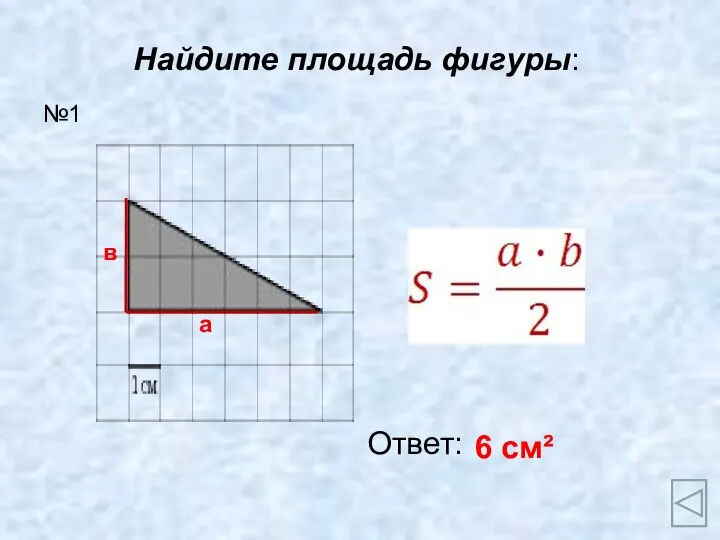 Формулы площадей
Формулы площадей Задача на тему: Прогрессия
Задача на тему: Прогрессия Неопределенный интеграл. Способы вычисления
Неопределенный интеграл. Способы вычисления Системы счисления
Системы счисления Правила с двумя решениями. Подход Неймана – Пирсона
Правила с двумя решениями. Подход Неймана – Пирсона Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и нас
Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и нас Весёлый ёжик. Дидактическая игра
Весёлый ёжик. Дидактическая игра Математическая сказка. Путешествие в сказку Царевна-лягушка
Математическая сказка. Путешествие в сказку Царевна-лягушка Презентация на тему Единицы массы (4 класс)
Презентация на тему Единицы массы (4 класс)  Числа по порялку
Числа по порялку Системы линейных дифференциальных уравнений
Системы линейных дифференциальных уравнений Математическая логика
Математическая логика Задачи на смеси
Задачи на смеси Логические задачки для дошкольников
Логические задачки для дошкольников Презентация на тему Итоговый зачет по математике (6 класс)
Презентация на тему Итоговый зачет по математике (6 класс)