Презентация на тему Парабола

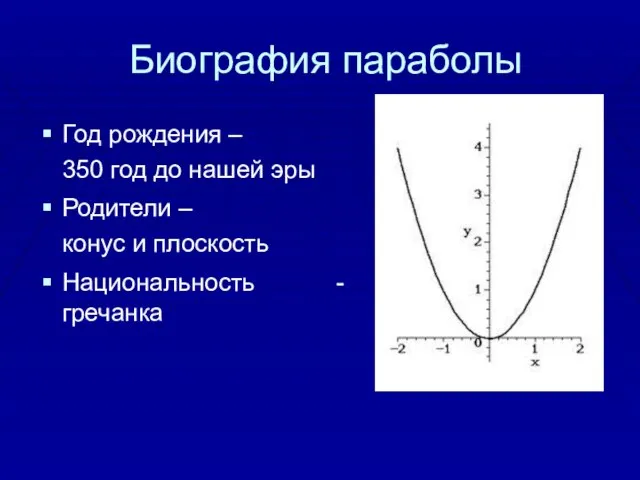
Биография параболы
Год рождения –
350 год до нашей эры
Родители –
конус и плоскость
Национальность -гречанка

Парабола
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.
Коническое сечение

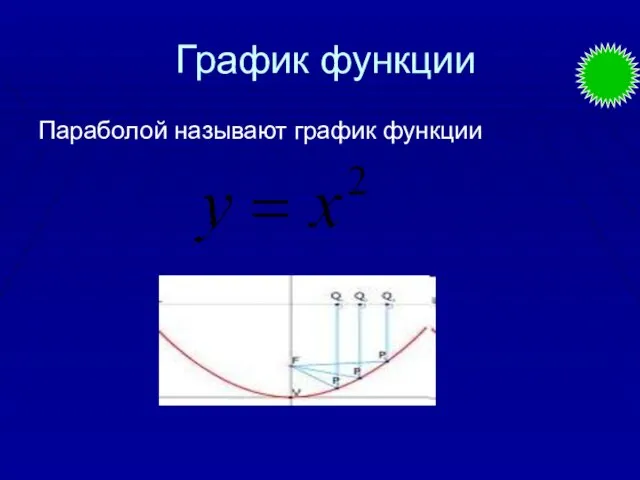
График функции
Параболой называют график функции

Парабола по точкам
Параболу можно построить «по точкам» с помощью циркуля и линейки, не зная уравнения и имея в наличии только фокус и директрису. Вершина является серединой отрезка между фокусом и директрисой.

ЭТО ДОЛЖЕН ЗНАТЬ КАЖДЫЙ!
Исследователи одним из первых источников называют Аристотеля. Стоики говорят о параболе в учении о тропах. В латинских риториках существует синонимичное по значению слово similitudo или collatio. Вплоть до поздней античности эти термины используются вместе с греческим вариантом.
В Ветхом завете и его толкованиях появляется синонимичное еврейское слово «машáль» (מָשָׁל). В раввинистической литературе термином «машаль» обозначались такие жанры, как притча и басня.

Парабола в природе

Парабола в космосе

Парабола в архитектуре

Парабола в творчестве художников