Квадратичная функция

Замечательное свойство параболы
Если в точке (0;0,25) поместить источник света, то лучи, отражаются от параболы параллельно оси Y.
Эту точку называют фокусом параболы.
Эта идея используется в автомобильных фарах.

Рассмотрим математическую модель
x – сторона квадрата
y – его площадь,
тогда y = x2
X – независимая переменная
y – зависимая переменная

Рассмотрим функцию y = x2
Дадим независимой переменной х конкретные значения и вычислим соответствующие значения зависимой переменной y.

Построим график функции
y = x2

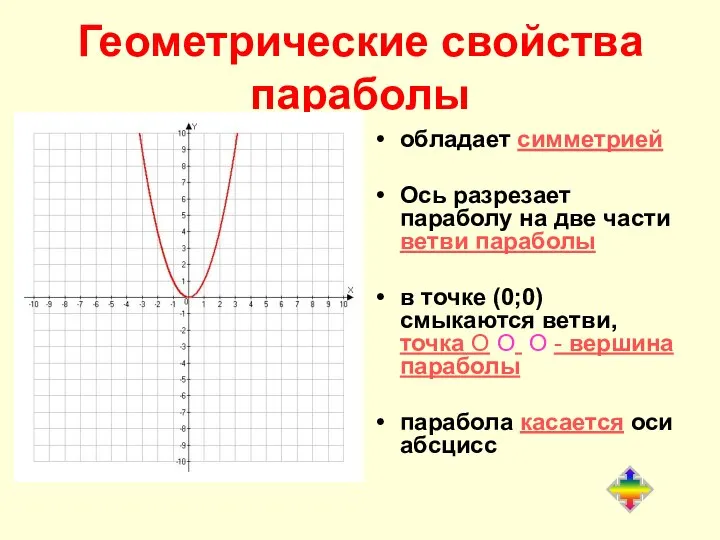
Геометрические свойства параболы
обладает симметрией
Ось разрезает параболу на две части ветви параболы
в точке (0;0) смыкаются ветви, точка О О О - вершина параболы
парабола касается оси абсцисс

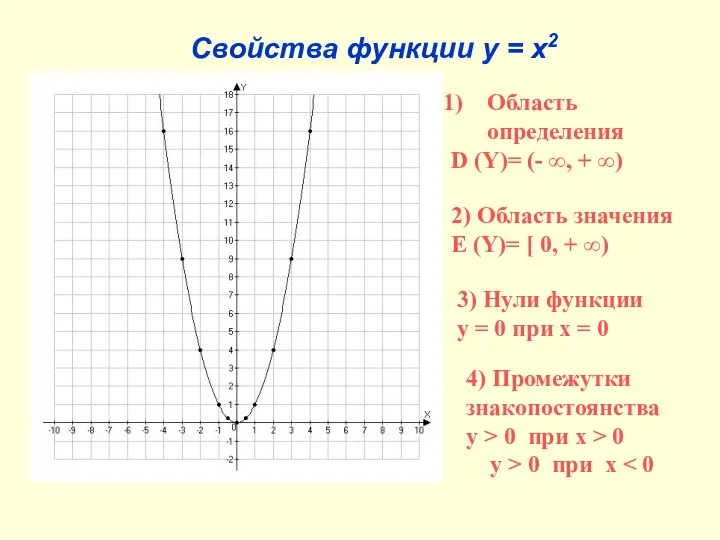
Свойства функции y = x2
3) Нули функции
y = 0 при x = 0
4) Промежутки знакопостоянства
y > 0 при x > 0
y > 0 при x < 0
2) Область значения E (Y)= [ 0, + ∞)
Область определения
D (Y)= (- ∞, + ∞)