Декартова система координат в пространстве

Определение
Упорядоченная система трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат в пространстве.

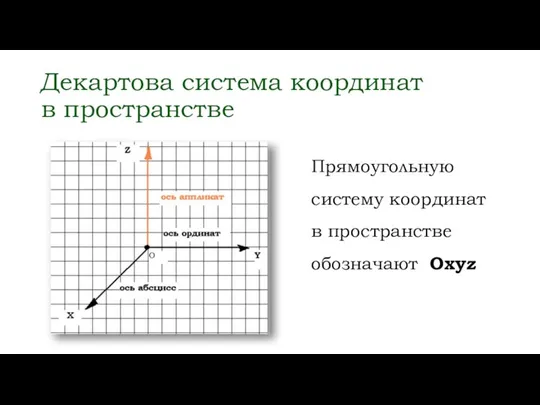
Декартова система координат
в пространстве
Прямоугольную систему координат в пространстве обозначают Охуz

Через каждые 2 оси координат проходят координатные плоскости:
xOy, xOz и yOz
Оz Оx

Каждая ось делится точкой О на два луча.
В соответствии с этим, лучи, направление которых совпадает с направлением оси, называют положительными полуосями, а оставшиеся лучи — отрицательными полуосями

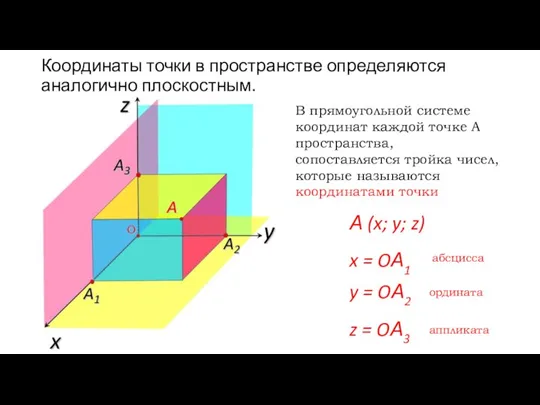
Координаты точки в пространстве определяются аналогично плоскостным.
В прямоугольной системе координат каждой точке А пространства, сопоставляется тройка чисел, которые называются координатами точки
А (x; y; z)

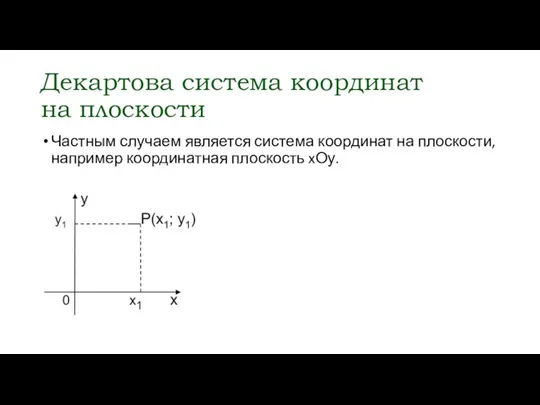
Декартова система координат
на плоскости
Частным случаем является система координат на плоскости, например координатная плоскость xОу.

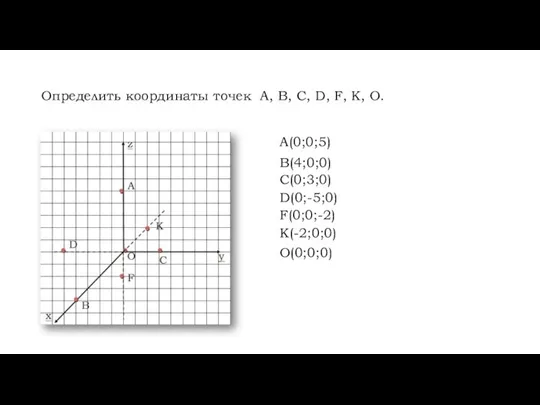
Определить координаты точек А, В, С, D, F, К, О.
А(0;0;5)
В(4;0;0)
С(0;3;0)
D(0;-5;0)
F(0;0;-2)
К(-2;0;0)
О(0;0;0)

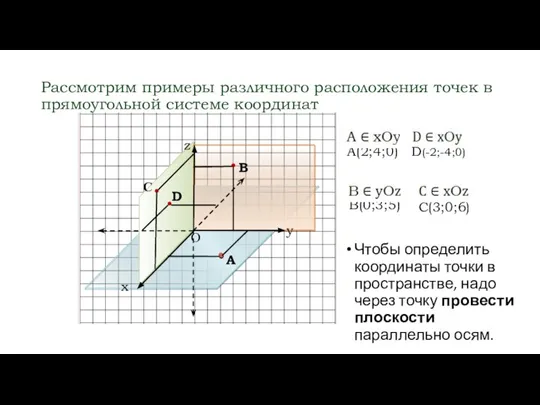
Рассмотрим примеры различного расположения точек в прямоугольной системе координат
А
О
А(2;4;0)
В
В(0;3;5)
С
С(3;0;6)
D(-2;-4;0)
D
Чтобы определить координаты точки в пространстве, надо через точку провести плоскости параллельно осям.

Задание 1:
По координатам точек
?(1;−1;0), ?(0;0;−3), ?(5;0;0),
?(−3;0;3), ?(0;−2;0), F(0;4;-6)
определить, какие из них лежат на той или иной координатной оси или в той или иной координатной плоскости.

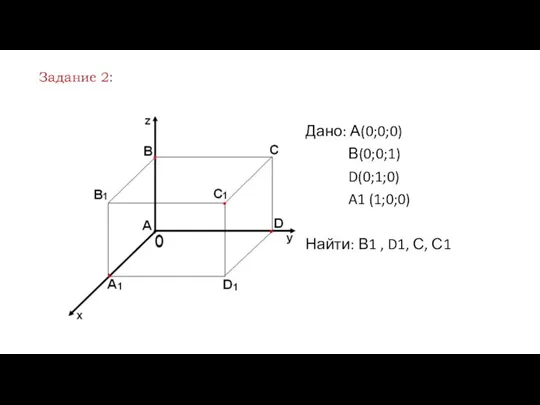
Дано: А(0;0;0)
В(0;0;1)
D(0;1;0)
A1 (1;0;0)
Найти: В1 , D1, С, С1
Задание 2: