Содержание
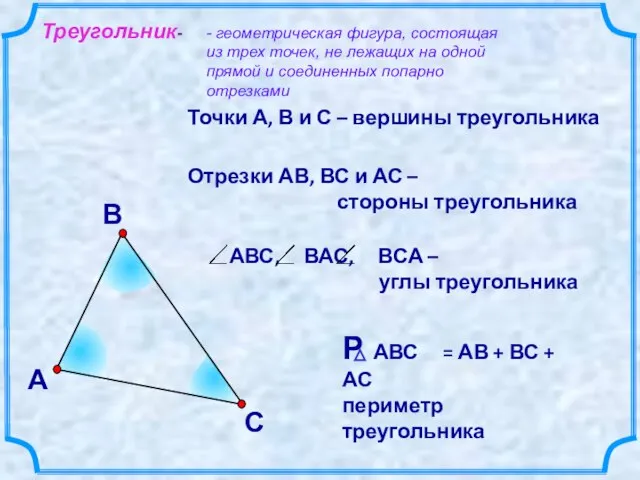
- 2. В А С Точки А, В и С – вершины треугольника Отрезки АВ, ВС и АС
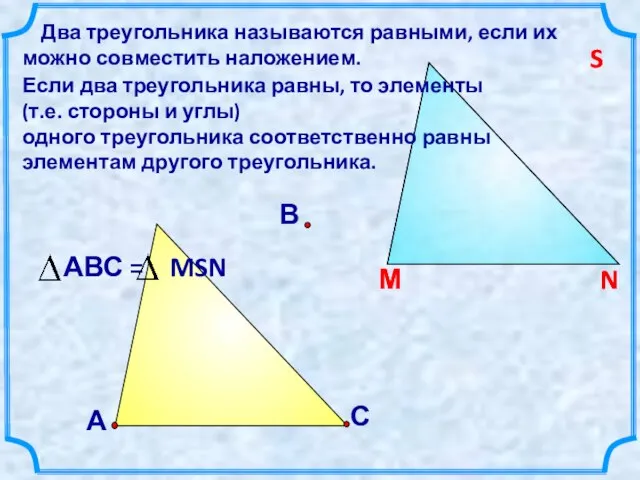
- 3. С В Два треугольника называются равными, если их можно совместить наложением. Если два треугольника равны, то
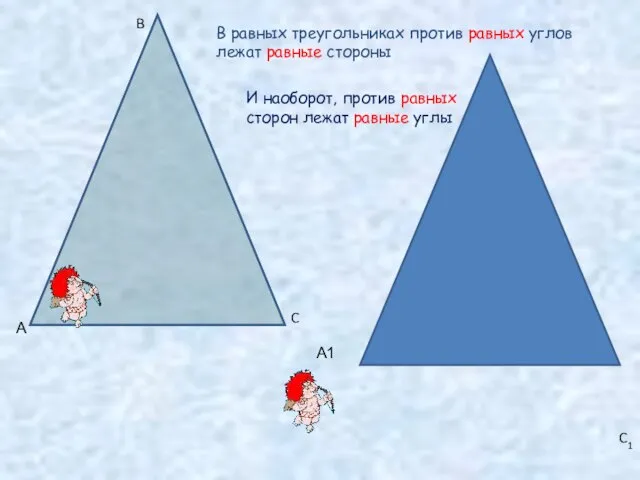
- 4. А B C B1 C1 В равных треугольниках против равных углов лежат равные стороны И наоборот,
- 5. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между
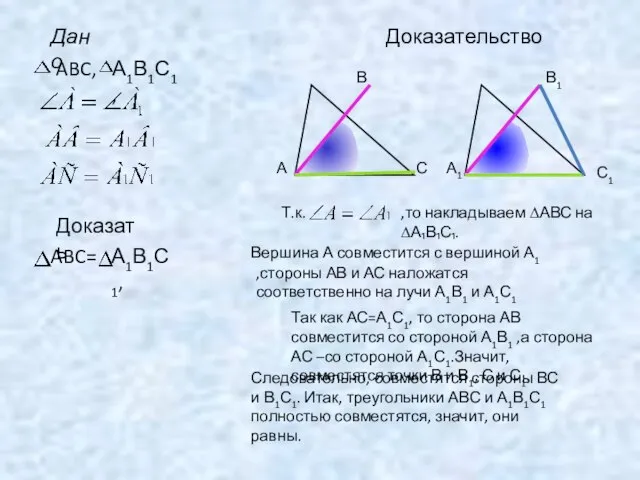
- 6. Доказать ABC= А1В1С1, Доказательство А В С А1 В1 С1 Т.к. ,то накладываем ∆АВС на ∆А₁В₁С₁.
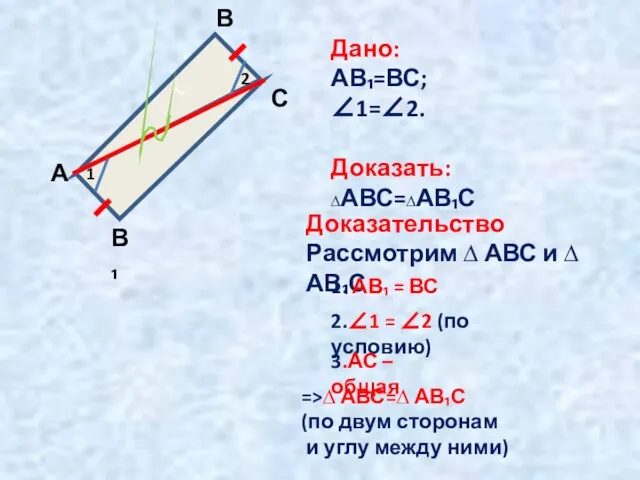
- 7. 1 1 2 А В С В₁ Дано: АВ₁=ВС; ∠1=∠2. Доказать: ∆АВС=∆АВ₁С Доказательство Рассмотрим ∆ АВС
- 8. Если Две стороны и угол между ними одного треугольника соответственно равны Двум сторонам и углу между
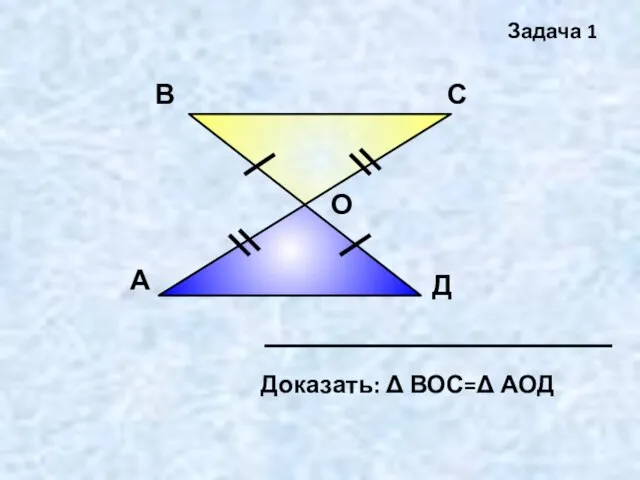
- 9. А В С Д О Задача 1
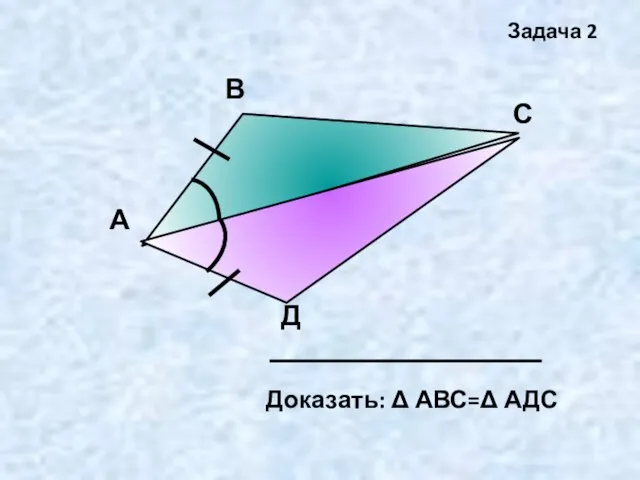
- 10. А В С Д Задача 2
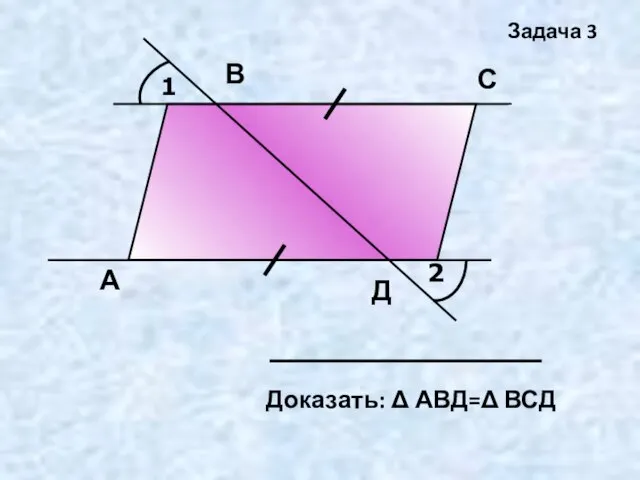
- 11. 1 2 А В С Д Задача 3
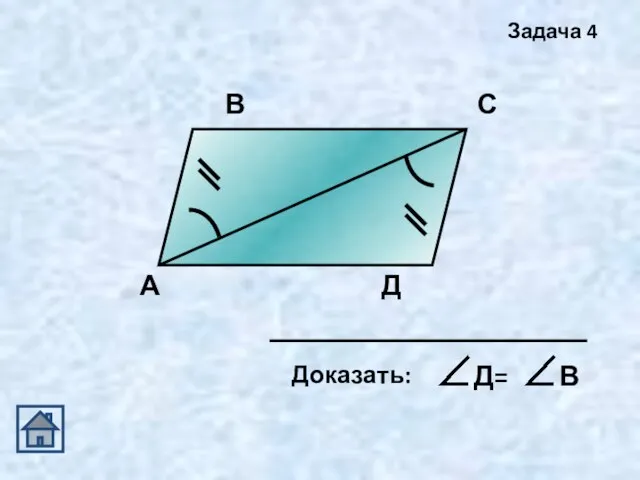
- 12. А В С Д Задача 4
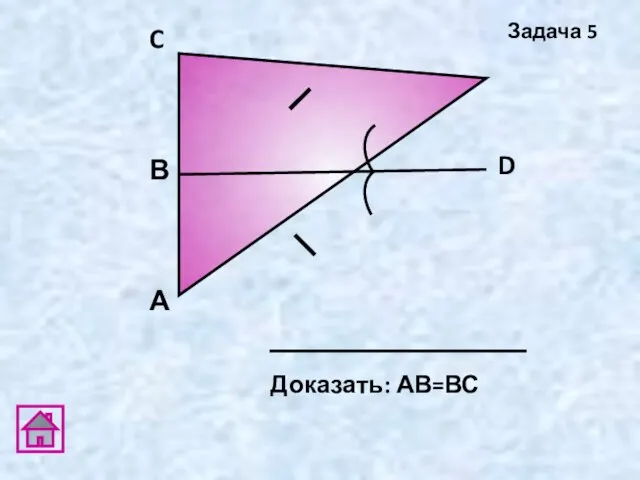
- 13. А D В C Доказать: АВ=ВС Задача 5
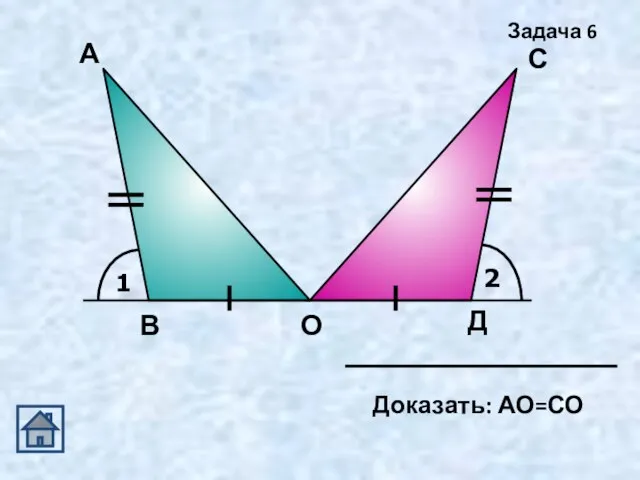
- 14. 1 2 А Д С О В Задача 6
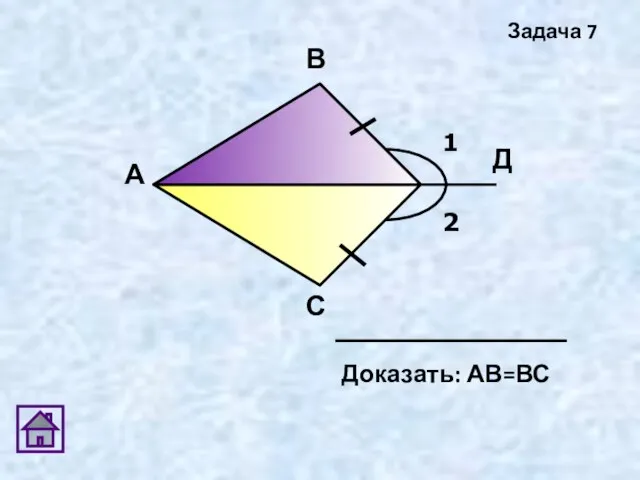
- 15. Задача 7
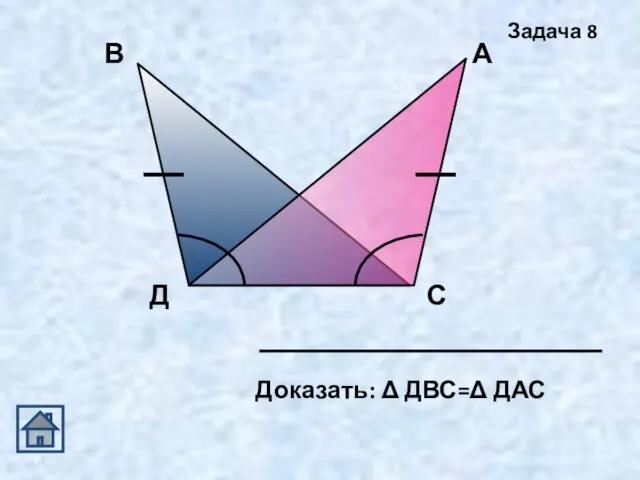
- 16. Доказать: Δ ДВС=Δ ДАС Задача 8
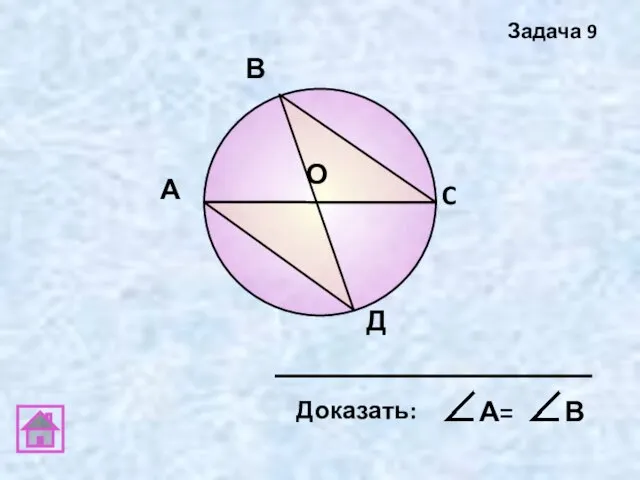
- 17. А В C Д О Задача 9
- 19. Скачать презентацию


 Физико-математический турнир. Интегрированный урок
Физико-математический турнир. Интегрированный урок ЕГЭ по профильной математике. Прототипы №3
ЕГЭ по профильной математике. Прототипы №3 Transformace. Ekvivalence
Transformace. Ekvivalence Метод следов. Построение следа секущей плоскости
Метод следов. Построение следа секущей плоскости Симметрия в технике
Симметрия в технике Устный счет на уроках математики
Устный счет на уроках математики Полярные координаты
Полярные координаты парні і непарні функції-1
парні і непарні функції-1 Действия со смешанными числами
Действия со смешанными числами Математика. Занятие 32
Математика. Занятие 32 Понятие ”тетраэдр”
Понятие ”тетраэдр” Случаи вычитания 15 -
Случаи вычитания 15 - Числа вокруг нас
Числа вокруг нас Интегрированный урок алгебры и экономики. 7 класс
Интегрированный урок алгебры и экономики. 7 класс Сравнение групп предметов. Свойства предметов (1 класс)
Сравнение групп предметов. Свойства предметов (1 класс) Размерные цепи
Размерные цепи Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД  Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска Примеры
Примеры Дисперсия случайной величины и ее свойства
Дисперсия случайной величины и ее свойства Приемы устного счета
Приемы устного счета Прямоугольник. Квадрат
Прямоугольник. Квадрат Физический и геометрический смысл производной
Физический и геометрический смысл производной Тесты свойств графических элементов в пространстве
Тесты свойств графических элементов в пространстве Функция у=log ах, ее свойства и график
Функция у=log ах, ее свойства и график Симметрия в искусстве
Симметрия в искусстве Пирамиды. Решение задач. C 12
Пирамиды. Решение задач. C 12 Пересекающиеся прямые. Отрезок и его длина
Пересекающиеся прямые. Отрезок и его длина