Содержание
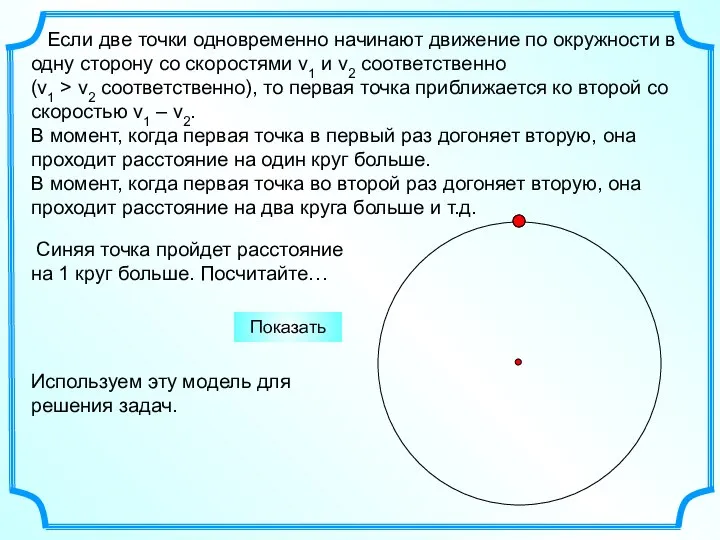
- 2. Если две точки одновременно начинают движение по окружности в одну сторону со скоростями v1 и v2
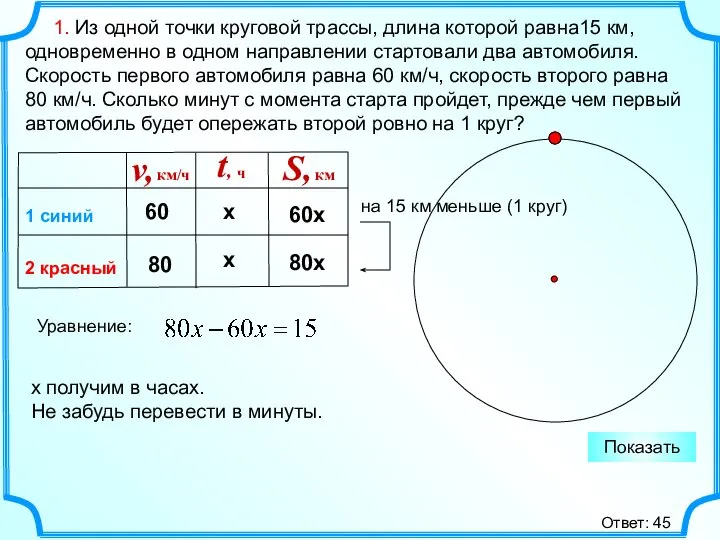
- 3. 1. Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два
- 4. 2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали
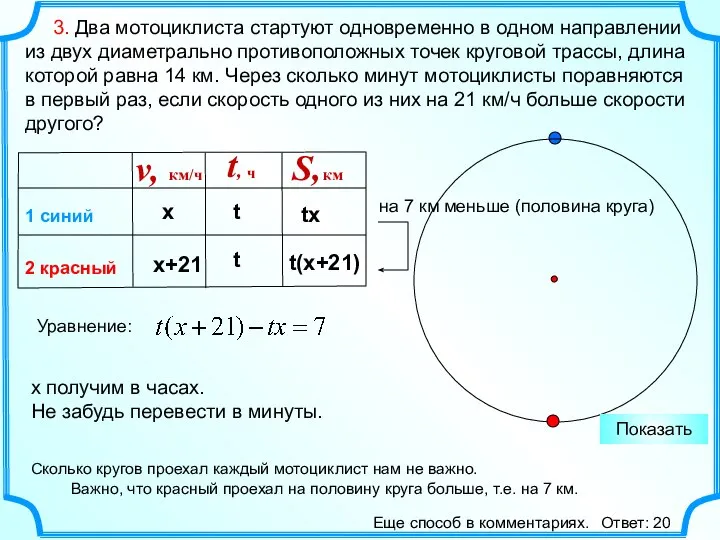
- 5. 3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина
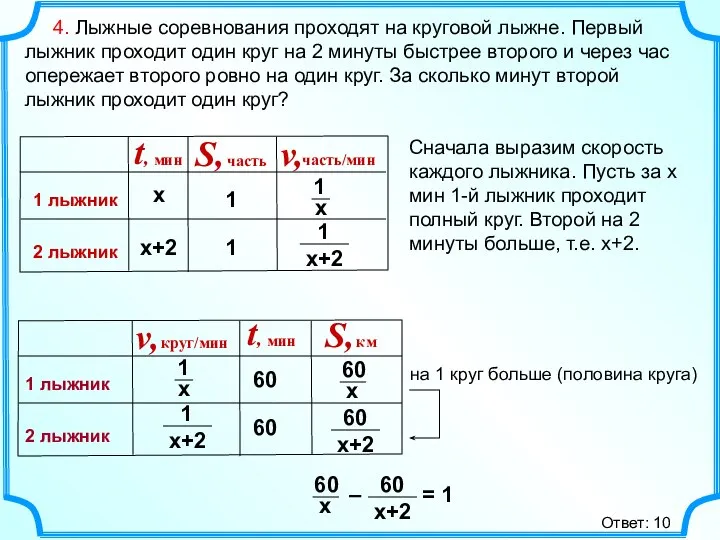
- 6. 4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее
- 7. 5. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали
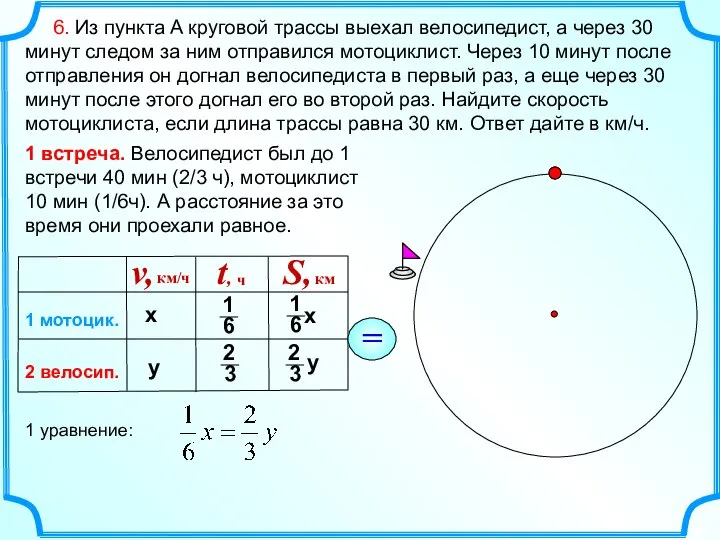
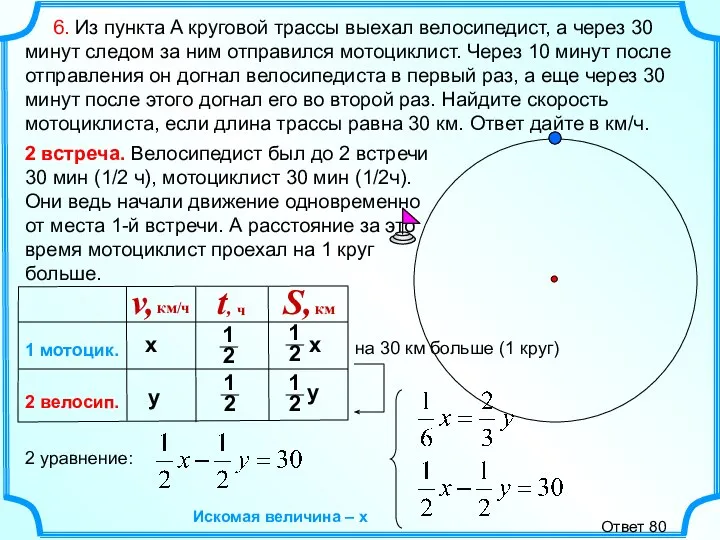
- 8. 6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился
- 9. 6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился
- 11. Скачать презентацию


 Понятие цилиндра
Понятие цилиндра Квадратичная функция у=х2 и ее свойства
Квадратичная функция у=х2 и ее свойства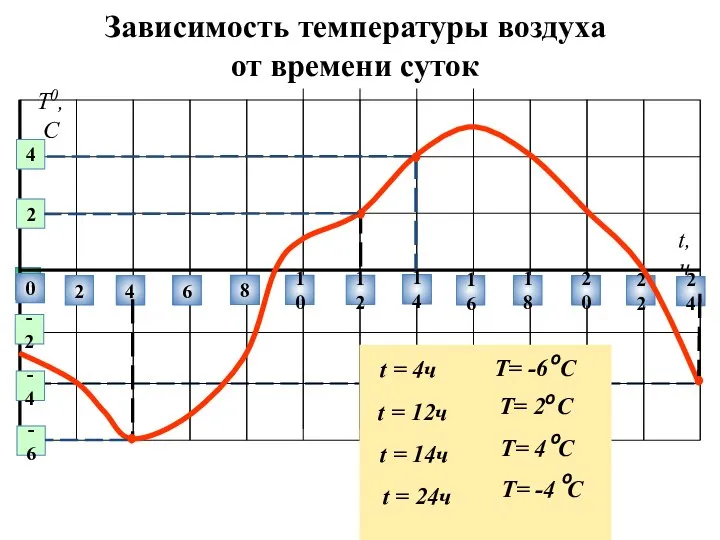 Зависимость температуры воздуха от времени суток
Зависимость температуры воздуха от времени суток Задачи на части
Задачи на части Осевая симметрия
Осевая симметрия Математическая игра Отгадайка
Математическая игра Отгадайка Найдите все значения параметра a,
Найдите все значения параметра a, А-11 Триг функции и их свойства 29.09.22 - копия
А-11 Триг функции и их свойства 29.09.22 - копия Евклидова геометрия
Евклидова геометрия Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Способ вычисления двойных интегралов путем сведения их к повторному интегралу
Способ вычисления двойных интегралов путем сведения их к повторному интегралу Ромб, квадрат
Ромб, квадрат Четырёхугольники. Задачи на готовых чертежах
Четырёхугольники. Задачи на готовых чертежах Презентация на тему Учим состав числа от 5 до 10
Презентация на тему Учим состав числа от 5 до 10  Matplotlib
Matplotlib Применение теоремы синусов
Применение теоремы синусов Математическая логика и теория алгоритмов. Алгебра логики. Часть 2
Математическая логика и теория алгоритмов. Алгебра логики. Часть 2 Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Решение прямоугольных треугольников
Решение прямоугольных треугольников Ряды
Ряды Презентация на тему Сдвиг графика функции y = x вдоль осей координат
Презентация на тему Сдвиг графика функции y = x вдоль осей координат  Гипотеза Пуанкаре
Гипотеза Пуанкаре Экзамен по математике
Экзамен по математике Подготовка к ГИА
Подготовка к ГИА Решение систем уравнений и неравенств графическим способом
Решение систем уравнений и неравенств графическим способом Презентация на тему Движение фигур в стереометрии
Презентация на тему Движение фигур в стереометрии  Презентация на тему Прямоугольный треуголиник: синус, косинус, тангенс угла
Презентация на тему Прямоугольный треуголиник: синус, косинус, тангенс угла