Слайд 2Делимость суммы на натуральное число
Если каждое из слагаемых делится на натуральное число,

то и сумма делится на натуральное число.
Например:
(12 + 60) : 12 = 12 : 12 + 60 : 12 = 1 + 5 = 6
(48 + 32) : 8 = 48 : 8 + 32 : 8 = 6 + 4 = 10
(52 + 26 + 39):13 = 52 : 13 + 26 : 13 + 39 : 13 = 4+2+3=9
(49а + 35с + 77) : 7 = 49а : 7 + 35с : 7 + 77 : 7 = 7а + 5с + 11
( а + b) : с = а : с + b : с
Слайд 3Делимость произведения на натуральное число
Если один из множителей делится на натуральное число,

то и произведение делится на натуральное число.
Например:
(65 * 52) : 13 = 65 : 13 * 52 = 5 * 52 = 260
(72 * 96) : 12 = 72 : 12 * 96 = 6 * 96 = 576
(65а * 130) : 13 = 65а : 13 * 130 = 5а *130 =650а
( а * b) : с = ( а : с) * b = а * ( b : с)
Слайд 4Признаки делимости на 2,5,10
Все натуральные числа запись которых оканчивается четной цифрой делится

на 2.
Все натуральные числа запись которых оканчивается цифрой 5 или цифрой 0 делится на 5.
Все натуральные числа запись которых оканчивается цифрой 0 делится на 10.
Слайд 5Признаки делимости на 3 и 9
Если сумма цифр делится на 3, то

и само число делится на 3.
522 делится на 3 так как 5 + 2 + 2 = 9, а 9 : 3 = 3
8136 делится на 3 так как 8 + 1 + 3 + 6 = 18, а 18 делится на 3
Если сумма цифр делится на 9, то и само число делится на 9.
1728 делится на 9, т.к. 1 + 7 + 2 + 8 = 18, а 18 делится на 9
8748 делится на 9, т.к. 8 + 7 + 4 + 8 = 27, а 27 делится на 9




 Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие reshenie_treugolnikov
reshenie_treugolnikov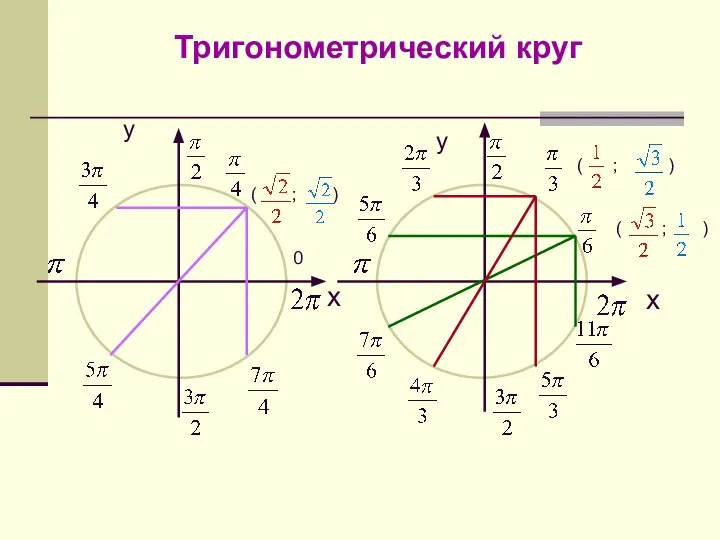 Тригонометрический круг
Тригонометрический круг Математика. Управление социальными системами .Тема 1. Векторная алгебра
Математика. Управление социальными системами .Тема 1. Векторная алгебра Последовательность чисел. Счет предметов. Сравнение предметов
Последовательность чисел. Счет предметов. Сравнение предметов Величины. Длина
Величины. Длина Четыре замечательные точки треугольника. 8 класс
Четыре замечательные точки треугольника. 8 класс Математическое моделирование природных комплексов Урюпинского района Волгоградской области
Математическое моделирование природных комплексов Урюпинского района Волгоградской области Квадратные неравенства
Квадратные неравенства Погрешность результата измерения
Погрешность результата измерения Решение неравенств. 8 класс
Решение неравенств. 8 класс Занимательная геометрия
Занимательная геометрия Материалы по теме Окружность и углы
Материалы по теме Окружность и углы Предмет и метод статистики
Предмет и метод статистики Цифровые средства измерения
Цифровые средства измерения Гласные звуки и буквы. Слова с буквой Э
Гласные звуки и буквы. Слова с буквой Э Подготовка к контрольной работе
Подготовка к контрольной работе Развитие интеллектуальных и творческих способностей одарённых учащихся в процессе преподавания математики
Развитие интеллектуальных и творческих способностей одарённых учащихся в процессе преподавания математики МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид
МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид Степенная функция
Степенная функция Пифагор Самосский
Пифагор Самосский Простейшие уравнения
Простейшие уравнения Правильный восьмиугольник
Правильный восьмиугольник Арифметико-логические устройства. Устройства управления
Арифметико-логические устройства. Устройства управления Основы линейной алгебры
Основы линейной алгебры Признаки параллельности прямых
Признаки параллельности прямых Большое развлечение с Винни и его друзьями
Большое развлечение с Винни и его друзьями Кубический корень
Кубический корень