Свойство биссектрисы угла. Свойства серединного перпендикуляра к отрезку

Цели урока:
Рассмотреть теорему о свойстве биссектрисы угла и её следствие, а также теорему о свойстве серединного перпендикуляра к отрезку и его следствия
Учить применять данные теоремы и следствия при решении задач.

Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является символом геометрии.
Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения - никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника.

C каждым треугольником связаны четыре точки:
• точка пересечения медиан;
• точка пересечения биссектрис;
• точка пересечения серединных перпендикуляров;
• точка пересечения высот.
Эти четыре точки называют замечательными точками треугольника.
Почему они «Замечательные»?
Это нам и предстоит узнать.

Свойство биссектрисы
Теорема (записать в тетрадь теорему и довазательство)
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Обратно:
Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

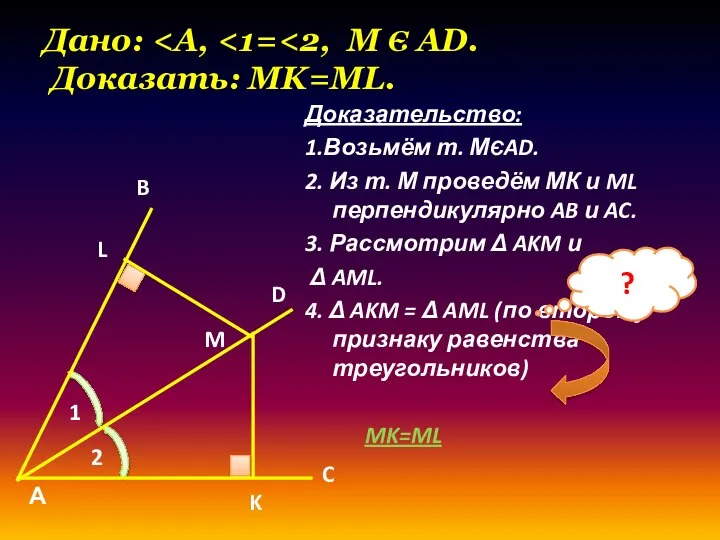
Дано:
Доказательство:
1.Возьмём т. МЄAD.
2. Из т. М проведём МК и ML перпендикулярно AB и AC.
3. Рассмотрим Δ AKM и
Δ AML.
4. Δ AKM = Δ AML (по второму признаку равенства треугольников)
MK=ML
?
А
2
1

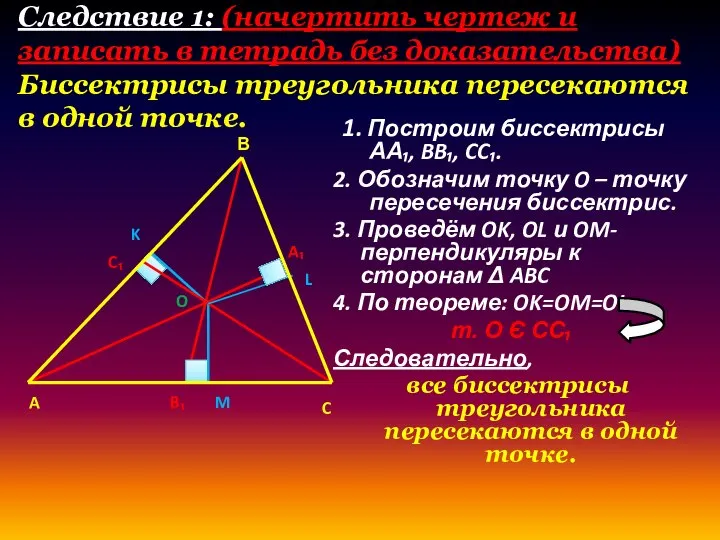
Следствие 1: (начертить чертеж и записать в тетрадь без доказательства)
Биссектрисы треугольника пересекаются в одной точке.
1. Построим биссектрисы АА₁, BB₁, CC₁.
2. Обозначим точку O – точку пересечения биссектрис.
3. Проведём OK, OL и OM-перпендикуляры к сторонам Δ ABC
4. По теореме: OK=OM=OL
т. О Є СС₁
Следовательно,
все биссектрисы треугольника пересекаются в одной точке.
O

Следствие 2: (зписать в тетрадь)
Геометрическим местом точек плоскости, лежащих внутри неразвернутого угла и равноудаленных от сторон угла, является биссектриса этого угла.

№ 676 б. (Записать задачу в тетрадь, самостоятельно справа написать дано)
Cтороны угла А, равного 90°, касаются окружности с центром О и радиусом r, ОА = 14 дм. Найдите: r.
Решение:
Проведём радиусы OP и OH из центра окружности в точки касания.
OP AP, OH AH
3. AO – биссектриса прямого угла А
Δ AOP – прямоугольный, равно– бедренный,
т.к <ОАР=90°:2 =45°
По теореме Пифагора:
AO²=OP²+AP²
AO²=r²+r²,
2r²=14², r=7√2.
Ответ: r=7√2дм.