Содержание
- 2. Элементарные функции алгебры логики x1 и x2 обозначают названия столбцов, f – символ, обозначающий отображение. Примечание.
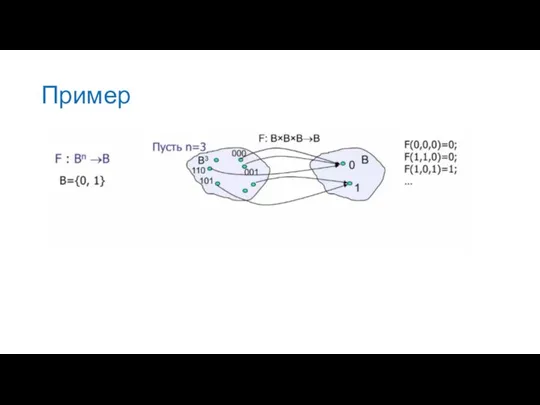
- 3. Пример
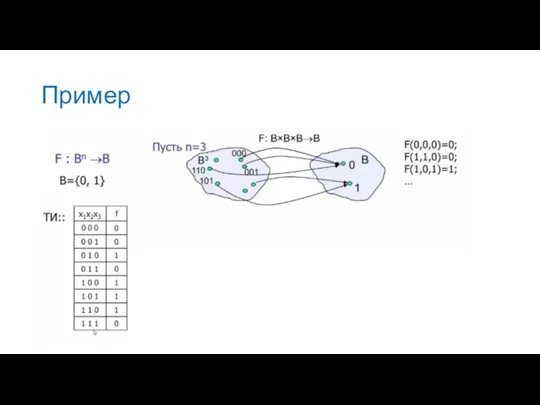
- 4. Пример
- 5. Классификация булевых функций Нульарные Унарные бинарные n-арные
- 6. Нульарные двоичные функции
- 7. Унарные функции
- 8. Классификация функций одной переменной
- 9. Рассмотрим классификацию функций двух переменных, приведенную в таблице: Классификация функций двух переменных
- 10. Классификация функций двух переменных
- 11. Классификация функций двух переменных
- 12. Классификация функций двух переменных
- 13. Классификация функций двух переменных
- 14. Стрелка Пирса и Штрих Шеффера
- 15. Существенные и несущественные переменные
- 16. Примеры
- 17. Примеры
- 18. Примеры Необходимо выяснить, какие переменные функции f (x, y, z) = 01011010 являются существенными, а какие
- 19. Примеры
- 20. Представление логической функции. Таблица истинности.
- 21. Пример Необходимо cоставить таблицу истинности f (x, y) = (x → y) v (y → x).
- 22. Пример Необходимо cоставить таблицу истинности f (x, y) = (x → y) v (y → x).
- 23. Пример
- 24. Пример
- 25. Сложности на практике
- 26. Решение В 1986 г. Было предложено использовать новые формы представления логических функций Binary Decision Diagram (BDD)
- 27. Представление логической функции. Геометрический способ. Для функции n – независимых логических переменных – рассматривается единичный n-мерный
- 28. Высказывание – повествовательное предложение, о котором можно сказать в данный момент, что оно истинно или ложно,
- 29. Для обозначения грамматических связок вводят символы, которые называют логическими (или пропозициональными) связками. Обычно рассматривают следующие логические
- 30. Понятие формулы алгебры логики Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения
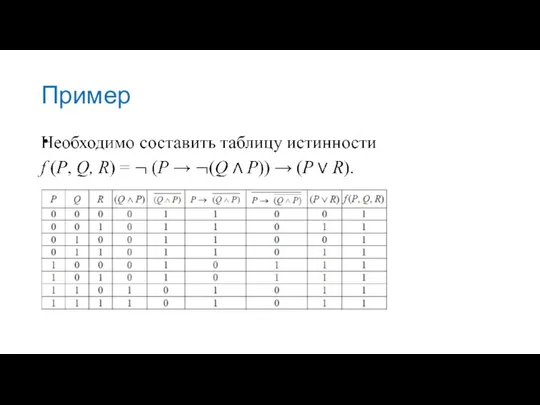
- 31. Пример
- 32. Пример
- 33. Пример
- 34. Пример Решение
- 35. Повторим вкратце Алгебра высказываний (Propositional logic) Высказывание (Proposition) – осмысленное предложение(sentence), о котором можно говорить, что
- 36. Повторим вкратце Правильно построенная формула (ППФ) АВ (Well-formed formula) Индуктивное определение Атом/элементарная формула (высказывательная переменная, логическая
- 37. Повторим вкратце Приоритет логических операций ¬, ∧, ∨, →, ↔
- 38. Логическое следствие
- 39. Логическое следствие
- 40. Логическое следствие
- 41. Логическое следствие
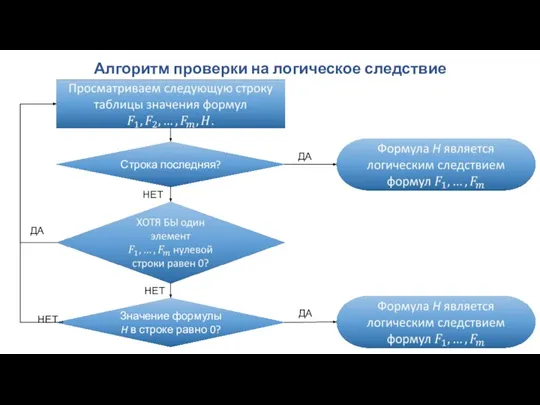
- 42. Алгоритм проверки на логическое следствие Значение формулы H в строке равно 0? Строка последняя? ДА ДА
- 43. Алгоритм проверки на логическое следствие
- 44. Пример 1
- 45. Пример 1
- 46. Пример 2
- 47. Пример 2
- 48. Эквивалентные формулы
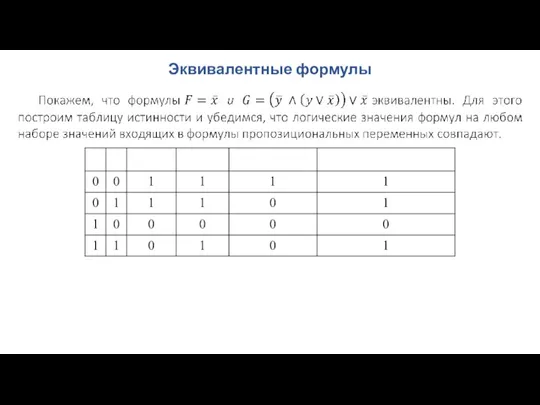
- 49. Эквивалентные формулы
- 50. Пример
- 51. Пример
- 52. Классы логических формул
- 53. Классы логических формул
- 54. Классы логических формул
- 55. Классы логических формул
- 56. Формула F называется выполнимой (опровержимой), если существует интерпретация, при которой формула F истинна (ложна). Эта терминология
- 57. Классы логических формул
- 58. Классы логических формул
- 59. Классы логических формул
- 60. Классы логических формул
- 61. Законы алгебры логики Булевой алгеброй, или алгеброй логики, называется множество всех логических функций с булевыми операциями:
- 62. Знание законов алгебры высказываний позволяет выполнять эквивалентные преобразования любых логических формул, т. е. такие преобразования, которые
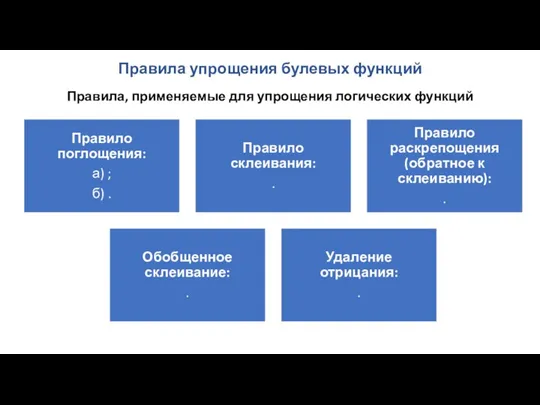
- 63. Правила упрощения булевых функций Правила, применяемые для упрощения логических функций
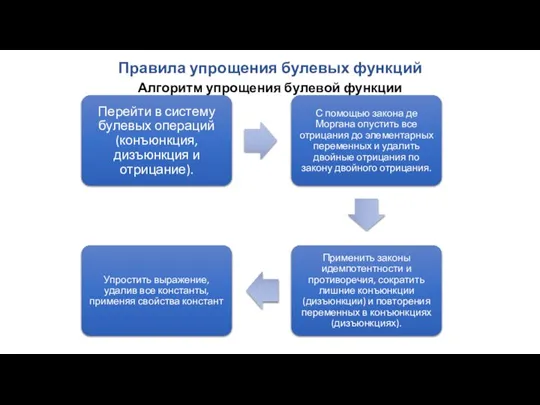
- 64. Правила упрощения булевых функций Алгоритм упрощения булевой функции
- 65. Пример
- 66. Пример
- 67. Нормальные формы формул алгебры логики Дизъюнктивная нормальная форма Элементарной конъюнкцией, или конъюнктивным одночленом от переменных A,
- 68. Нормальные формы формул алгебры логики Конъюнктивная нормальная форма
- 69. Алгоритм приведения к нормальной форме Шаг 2. Продвинуть отрицание до элементарной формулы (пропозициональной переменной) по законам
- 70. Пример
- 71. Пример Решение
- 72. Пример
- 73. Пример Решение
- 74. Пример
- 75. Пример
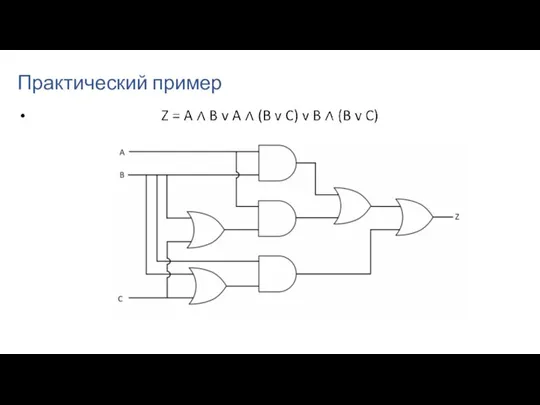
- 76. Практический пример
- 85. Теорема об эквивалентной формуле с тесными отрицаниями Для любой ППФ алгебры высказываний существует эквивалентная ей формула
- 86. Теорема об эквивалентной формуле с тесными отрицаниями Доказательство: Доказательство индукцией по числу логических связок, входящих в
- 87. Теорема об эквивалентной формуле с тесными отрицаниями Доказательство: n ≤ N,N ∈ ℕ n = N
- 88. Теорема об эквивалентной формуле с тесными отрицаниями Доказательство: Если A≡¬B, то возможны следующие случаи: B≡ ¬D,
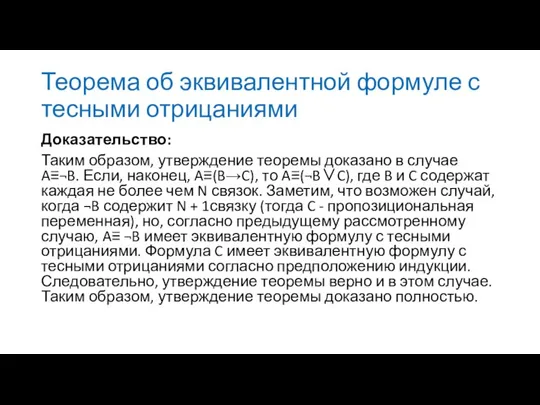
- 89. Теорема об эквивалентной формуле с тесными отрицаниями Доказательство: Таким образом, утверждение теоремы доказано в случае A≡¬B.
- 90. Теорема о существовании эквивалентной ДНФ Для любой ППФ АВ существует эквивалентная ей ДНФ. Доказательство. Согласно теореме
- 91. Теорема о существовании эквивалентной КНФ Для любой ППФ АВ существует эквивалентная ей КНФ.
- 92. Теорема о виде тождественно ложной ДНФ Если A – тождественно ложная ДНФ, то любая ее элементарная
- 93. Правила получения тавтологий Правило заключения (modus ponens) Правило подстановки
- 94. Правило заключения (modus ponens) Также называется правилом отделения Теорема: Если формулы F и F→H являются тавтологиями,
- 95. Правило заключения (modus ponens)
- 96. Правило подстановки
- 97. Алфавит - любое непустое не более чем счетное множество, элементы которого будем называть символами (буквами). Слово
- 98. Алфавит - любое непустое не более чем счетное множество, элементы которого будем называть символами (буквами). Слово
- 99. Совершенные нормальные формулы Основные способы задания булевых функций: Аналитический Истинностные таблицы Как перейти от ТИ к
- 100. Совершенные нормальные формы Если каждая элементарная конъюнкция (или элементарная дизъюнкция) формулы содержит символы всех пропозициональных переменных,
- 101. СДНФ ДНФ, в которой каждая элементарная конъюнкция зависит ото всех входящих в нее пропозициональных переменных и
- 102. СКНФ КНФ, в которой каждая элементарная дизъюнкция зависит от всех входящих в нее пропозициональных переменных и
- 103. Совершенные нормальные формы Алгоритм преобразования ДНФ к виду СДНФ
- 104. Совершенные нормальные формы Пример
- 105. Решение Совершенные нормальные формы Пример
- 106. Совершенные нормальные формы Алгоритм преобразования KНФ к виду СKНФ
- 107. Совершенные нормальные формы
- 108. Совершенные нормальные формы
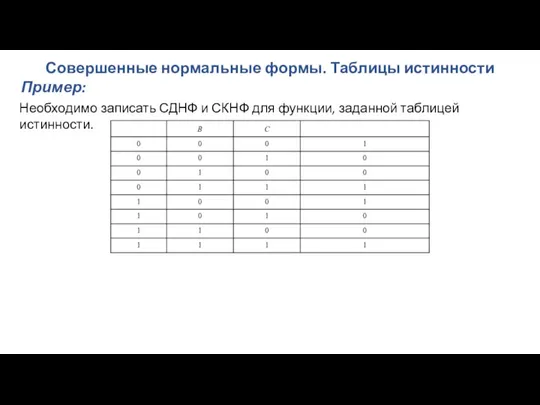
- 109. Совершенные нормальные формы. Таблицы истинности Элементарные конъюнкции СДНФ формируются для значений формулы 1. Число элементарных конъюнкций
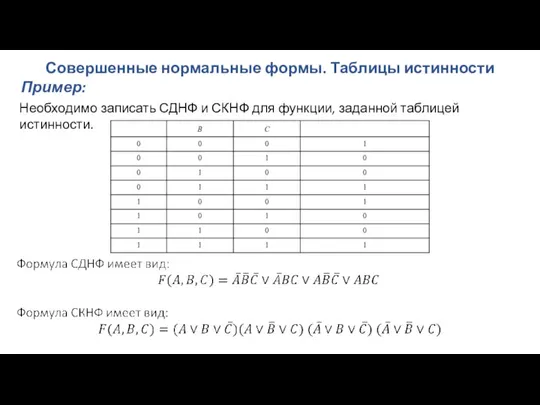
- 110. Совершенные нормальные формы. Таблицы истинности Необходимо записать СДНФ и СКНФ для функции, заданной таблицей истинности. Пример:
- 111. Совершенные нормальные формы. Таблицы истинности Необходимо записать СДНФ и СКНФ для функции, заданной таблицей истинности. Пример:
- 112. Теорема о существовании эквивалентной КНФ Для любой ППФ АВ существует эквивалентная ей КНФ. Доказательство: аналогично доказательству
- 113. Теорема о виде тождественно ложной ДНФ
- 114. Теорема о виде тождественно истинной КНФ
- 115. Условия существования с.д.н.ф., с.к.н.ф Теорема 2. Для любой опровержимой п.п.ф. существует эквивалентная с.к.н.ф. Кроме доказанных теорем
- 116. Условия существования с.д.н.ф., с.к.н.ф
- 117. Понятие логического высказывания в АВ
- 118. Понятие логического высказывания в АВ
- 119. Понятие логического высказывания в АВ
- 120. Понятие логического высказывания в АВ Пример
- 121. Непротиворечивые (выполнимые) и противоречивые (невыполнимые) множества посылок
- 122. Непротиворечивые (выполнимые) и противоречивые (невыполнимые) множества посылок
- 123. Установление факта логического следствия из данного множества посылок
- 124. Установление факта логического следствия из данного множества посылок
- 125. Установление факта логического следствия из данного множества посылок
- 126. Основные теоремы о логическом следствии
- 127. Основные теоремы о логическом следствии
- 128. Основные теоремы о логическом следствии
- 129. Основные теоремы о логическом следствии
- 130. Основные теоремы о логическом следствии
- 131. Основные теоремы о логическом следствии
- 132. Основные теоремы о логическом следствии
- 133. Основные теоремы о логическом следствии
- 134. Основные теоремы о логическом следствии
- 135. Основные теоремы о логическом следствии
- 136. Основные теоремы о логическом следствии
- 138. Скачать презентацию





















































































































 Метод Гаусса
Метод Гаусса Тренажер по логарифмам
Тренажер по логарифмам Пирамида – это многогранник, составленный из n-угольника
Пирамида – это многогранник, составленный из n-угольника Правильные многогранники
Правильные многогранники Презентация на тему Методы решения квадратных уравнений
Презентация на тему Методы решения квадратных уравнений  Задача по математике (1 класс)
Задача по математике (1 класс) Основы эконометрического моделирования
Основы эконометрического моделирования Физическое и математическое моделирование
Физическое и математическое моделирование Вычитание натуральных чисел
Вычитание натуральных чисел Новогодняя сказка в Стране математики. Для детей 5-ти лет
Новогодняя сказка в Стране математики. Для детей 5-ти лет Приём вычитания вида 15 -
Приём вычитания вида 15 - 1ce713f2e27cb837f4d7376560237c07
1ce713f2e27cb837f4d7376560237c07 Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Разложение вектора по базису
Разложение вектора по базису Задачи с параметрами.Расположение корней квадратного трёхчлена
Задачи с параметрами.Расположение корней квадратного трёхчлена Краткая история появления и развития пределов
Краткая история появления и развития пределов Центральная и осевая симметрия
Центральная и осевая симметрия Презентация на тему Формулы суммы и разности синуса и косинуса
Презентация на тему Формулы суммы и разности синуса и косинуса  Части множества
Части множества Угол между прямыми в пространстве
Угол между прямыми в пространстве Стандартизированные коэффициенты регрессии
Стандартизированные коэффициенты регрессии Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Булева алгебра
Булева алгебра Тайна табурета деда. Исследовательская работа студентов
Тайна табурета деда. Исследовательская работа студентов Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014
Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014 Производная степенной функции с действительным показателем
Производная степенной функции с действительным показателем Дюжина задач на параметры
Дюжина задач на параметры Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике