Делимость целых чисел

НА 2
На 2 делятся все четные натуральные числа, например: 172, 94,67 838.
НА 3
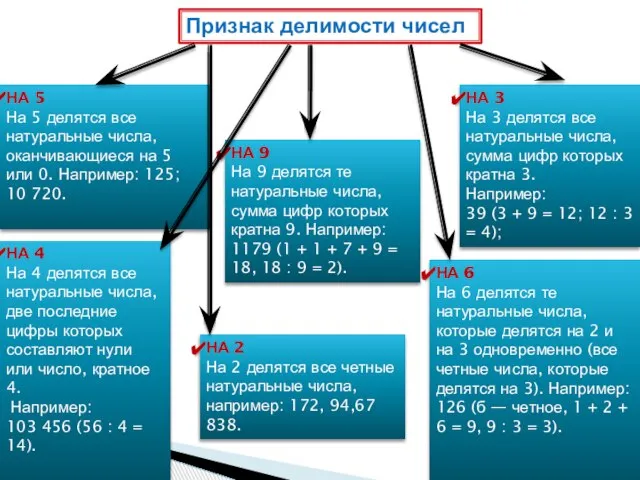
На 3 делятся все натуральные числа, сумма цифр которых кратна 3.
Например:
39 (3 + 9 = 12; 12 : 3 = 4);
НА 4
На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4.
Например:
103 456 (56 : 4 = 14).
НА 5
На 5 делятся все натуральные числа, оканчивающиеся на 5 или 0. Например: 125; 10 720.
НА 6
На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно (все четные числа, которые делятся на 3). Например: 126 (б — четное, 1 + 2 + 6 = 9, 9 : 3 = 3).
Признак делимости чисел
НА 9
На 9 делятся те натуральные числа, сумма цифр которых кратна 9. Например:
1179 (1 + 1 + 7 + 9 = 18, 18 : 9 = 2).

Признак делимости чисел
НА 10
На 10 делятся все натуральные числа, оканчивающиеся на 0. Например: 30; 980; 1 200; 1 570.
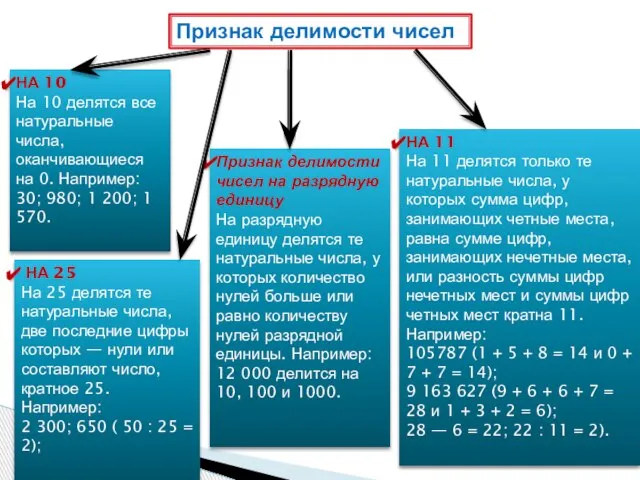
НА 11
На 11 делятся только те натуральные числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11. Например:
105787 (1 + 5 + 8 = 14 и 0 + 7 + 7 = 14);
9 163 627 (9 + 6 + 6 + 7 = 28 и 1 + 3 + 2 = 6);
28 — 6 = 22; 22 : 11 = 2).
НА 25
На 25 делятся те натуральные числа, две последние цифры которых — нули или составляют число, кратное 25. Например:
2 300; 650 ( 50 : 25 = 2);
Признак делимости чисел на разрядную единицу
На разрядную единицу делятся те натуральные числа, у которых количество нулей больше или равно количеству нулей разрядной единицы. Например: 12 000 делится на 10, 100 и 1000.

1 способ:
Для того, чтобы натуральное число делилось на 7 необходимо и достаточно, чтобы алгебраическая сумма чисел, образующих нечётные группы по три цифры (начиная с единиц) взятых со знаком «+» и чётных со знаком «-» делилась на семь.
Например: число 689255.
первая группа со знаком «+» 689, вторая со знаком «-» 255. Отсюда 689—255 = 434. Так как 434 : 7 = 62, то 689255 делится на 7.
2 способ:
Нужно последнюю цифру числа умножить на 2 и вычесть из «числа, оставшегося без последней цифры». Если получившееся число делится на 7, то и само число делится на 7.
Например: число 689255.
последняя цифра 5, значит 68925 – 2·5 = 68915
последняя цифра 5, значит 6891 – 2·5 = 6881
последняя цифра 1, значит 688 – 2·1 = 686
последняя цифра 6, значит 68 – 2·6 = 56
56 – делится на 7, значит 689255 делится на 7.
Признаки делимости на 7

1 способ:
Число делится на 13, если знакопеременная сумма чисел, образованных тройками его цифр, взятыми с конца (последнее число со знаком +), делится на 13.
Например: число 112567.
первая группа со знаком «+» 567, вторая со знаком «-» 112. Отсюда 567—112 = 455. Так как 455 : 13 = 35, то 112567 делится на 13.
2 способ:
Нужно взять последнюю цифру числа, умножить ее на 4 и прибавить к «числу, оставшемуся без последней цифры». Если получившееся число делится на 13, то и само число делится на 13.
Например: число 112567.
последняя цифра 7, значит 11256 + 7·4 = 11284
последняя цифра 4, значит 1128 + 4·4 = 1144
последняя цифра 4, значит 114 + 4·4 = 130
130 делится на 13, значит 112567 делится на 13.
Признак делимости на 13

1 способ:
Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17.
Например: число 29053
единиц 3, значит 2905+12·3=2941
единиц 1, значит 294+12·1=306
единиц 6, значит 30+12·6=102
единиц 2, значит 10+12·2=34
Так как 34 делится на 17, то и 29053 делится на 17).
2 способ:
Нужно взять последнюю цифру числа, умножить ее на 5 и вычесть из «числа, оставшегося без последней цифры». Если получившееся число делится на 17, то и само число делится на 17.
Например: число 29053
последняя цифра 3, значит 2905 – 5·3 = 2890
последняя цифра 0, значит 289 – 5·0 = 289
последняя цифра 4, значит 28 – 5·9 = – 17
– 17 делится на 17, значит 29053 делится на 17.
Признак делимости на 17