Содержание
- 2. ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ Логика – наука о формах и способах мышления. Основными формами мышления являются
- 3. Логика — это наука, изучающая законы и формы мышления. Алгебра логики — это математический аппарат, с
- 4. ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ Высказывание не может быть выражено повелительным или вопросительным предложением, так как оценка
- 5. ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть 0
- 6. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ В основе булевой алгебры лежат 16 основных функций. Наиболее часто применяемые из них:
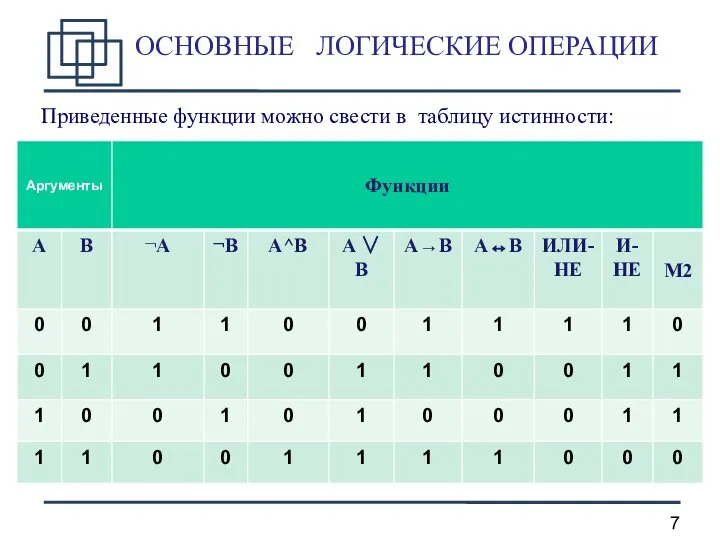
- 7. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Приведенные функции можно свести в таблицу истинности:
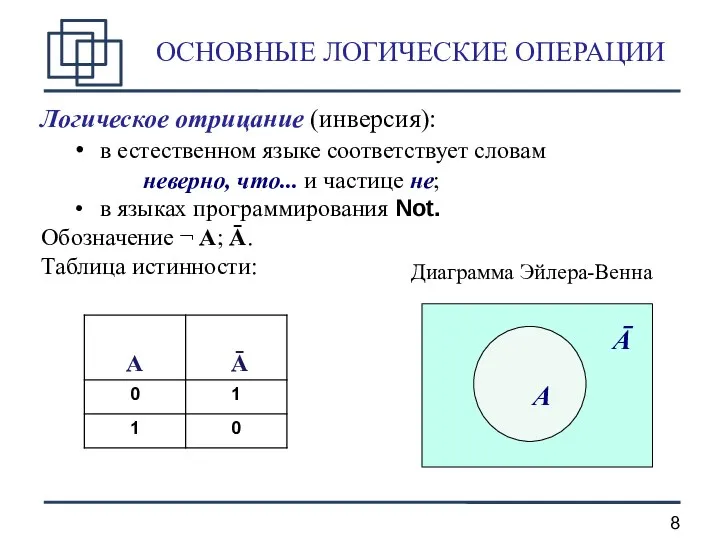
- 8. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое отрицание (инверсия): в естественном языке соответствует словам неверно, что... и частице не;
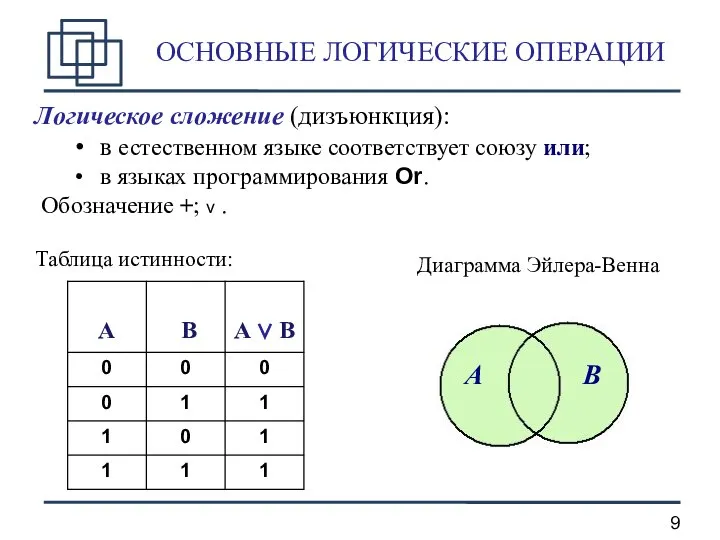
- 9. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое сложение (дизъюнкция): в естественном языке соответствует союзу или; в языках программирования Or.
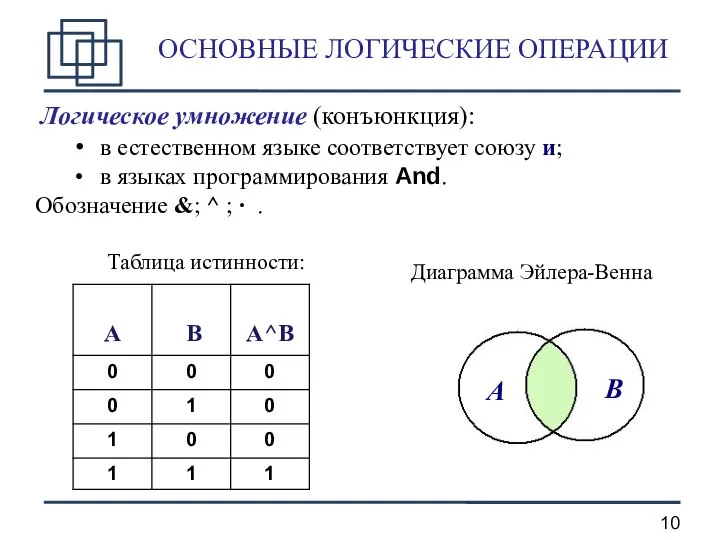
- 10. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое умножение (конъюнкция): в естественном языке соответствует союзу и; в языках программирования And.
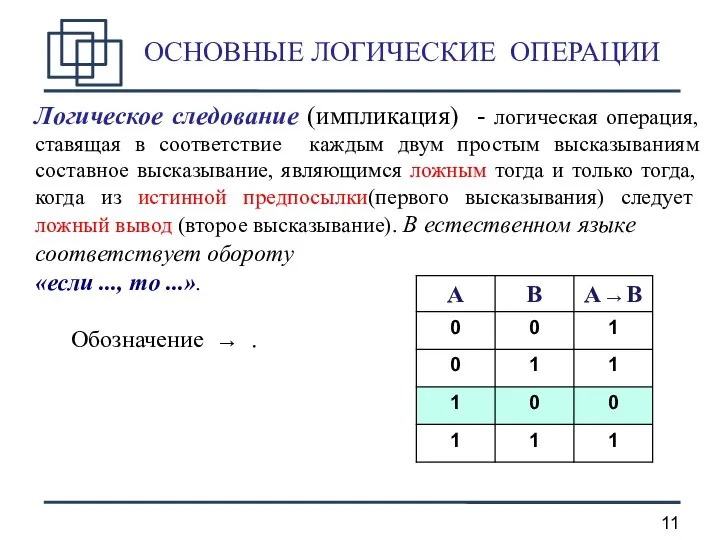
- 11. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое следование (импликация) - логическая операция, ставящая в соответствие каждым двум простым высказываниям
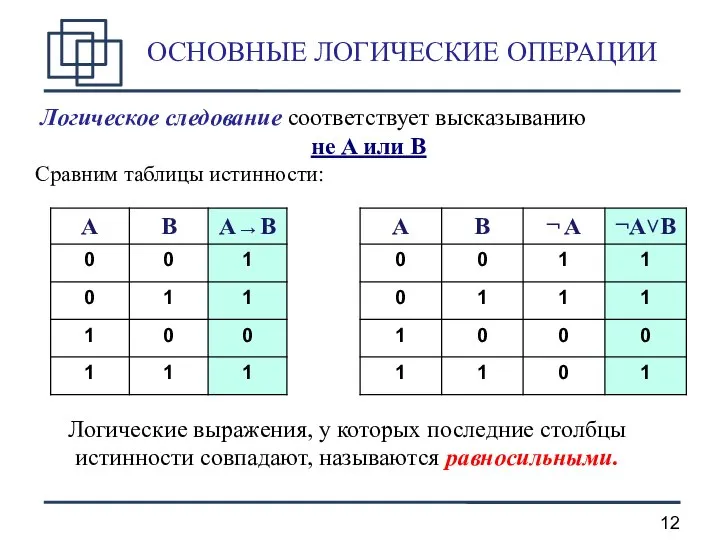
- 12. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое следование соответствует высказыванию не A или B Сравним таблицы истинности: Логические выражения,
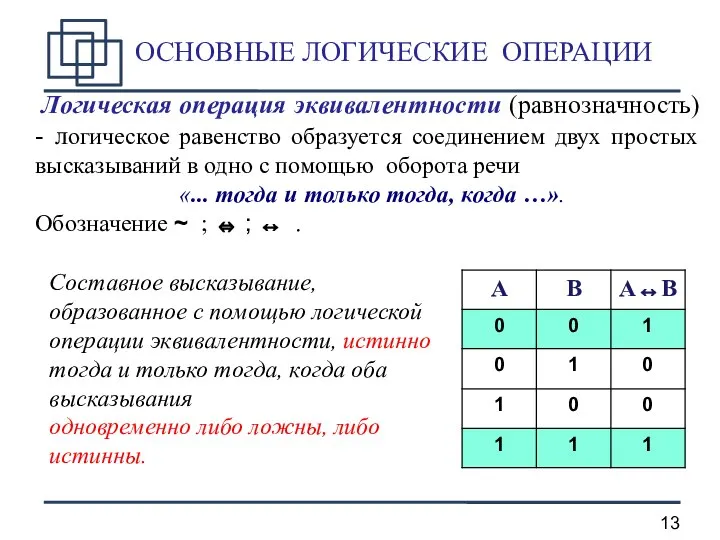
- 13. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическая операция эквивалентности (равнозначность) - логическое равенство образуется соединением двух простых высказываний в
- 14. ПРИОРИТЕТ ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ Логическое отрицание (инверсия) – «не»; ¬ ; ¯ . Логическое умножение (конъюнкция)
- 15. ТАБЛИЦЫ ИСТИННОСТИ Таблица истинности определяет истинность или ложность логической функции при всех возможных комбинациях исходных значений
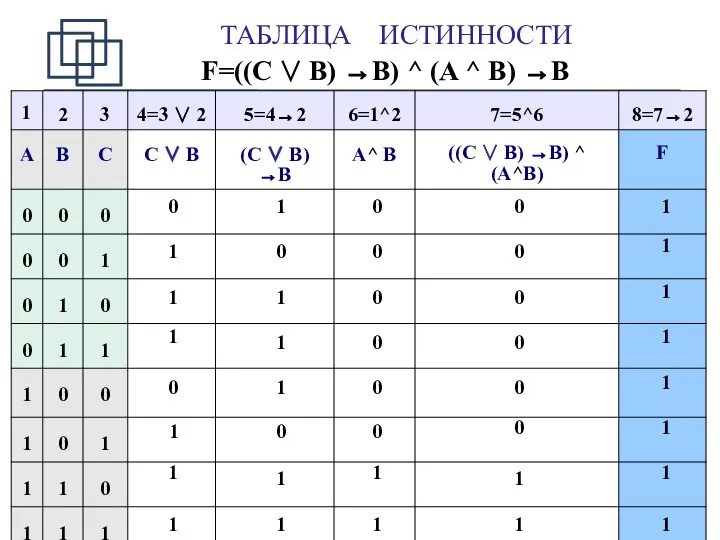
- 16. ТАБЛИЦЫ ИСТИННОСТИ Пример. Определить истинность формулы F=((C ∨ B) →B)^ (A^ B) →B Формула является тождественно
- 17. ТАБЛИЦА ИСТИННОСТИ F=((C ∨ B) →B) ^ (A ^ B) →B 0 1 1 1 0
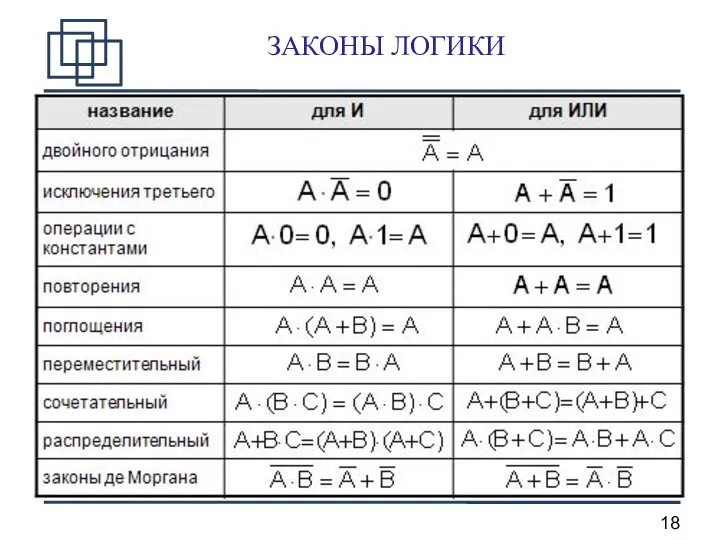
- 18. ЗАКОНЫ ЛОГИКИ
- 19. Задание 1. Для какого из указанных значений X истинно высказывание ¬((X > 2)→(X > 3))? 1)
- 20. Определим порядок действий: сначала вычисляются результаты отношений в скобках, затем выполняется импликация (поскольку есть «большие» скобки),
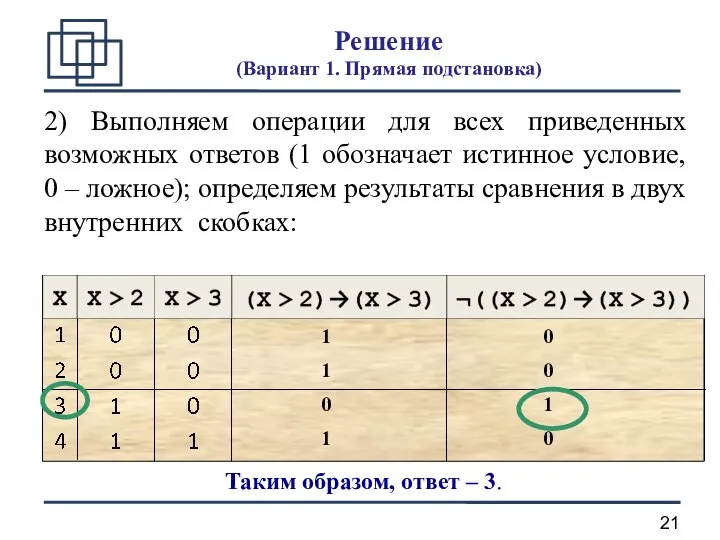
- 21. 2) Выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); определяем
- 22. Возможные ловушки и проблемы Можно «забыть» отрицание (помните, что правильный ответ – всего один!) Можно перепутать
- 23. Решение (Вариант 2. Упрощение выражения) ¬((X > 2)→(X > 3)) Обозначим простые высказывания буквами: A =
- 24. Возможные проблемы Нужно помнить законы логики (например, формулы де Моргана). При использовании формул де Моргана нужно
- 25. Выводы В данном случае, наверное, проще первый вариант решения (прямая подстановка всех предложенных ответов). Второй вариант
- 26. A8 (базовый уровень, время – 1 мин) Укажите, какое логическое выражение равносильно выражению A ∧ ¬(¬B
- 27. Решение (Вариант 1. Использование законов де Моргана) Перепишем заданное выражение в других обозначениях: A ∧ ¬(¬B
- 28. Возможные ловушки и проблемы Серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений, поэтому
- 29. Решение (Вариант 2. Через таблицы истинности, если забыли формулы де Моргана) Перепишем заданное выражение в других
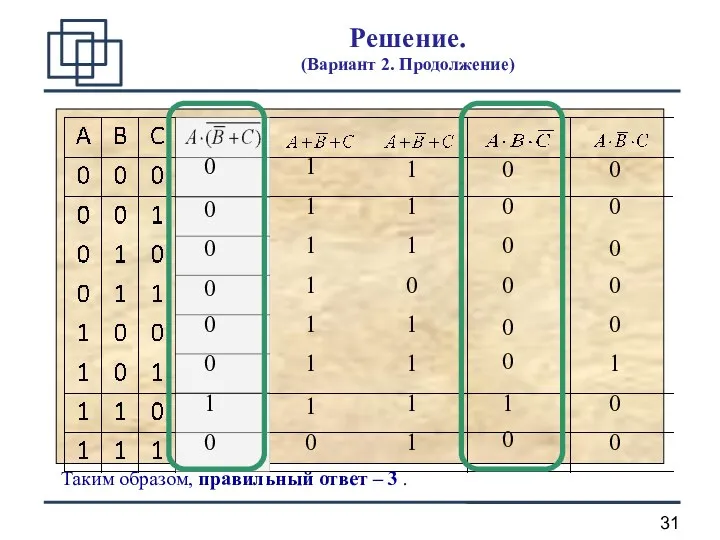
- 30. Решение (Вариант 2. Продолжение) Поэтому можно составить таблицы истинности для исходного выражения и всех ответов и
- 31. Решение. (Вариант 2. Продолжение) 1 0 0 0 0 0 0 0 0 1 1 1
- 32. Решение (комментарий к таблице) Исходное выражение истинно только тогда, когда и , то есть только при
- 33. Аналогично выражение ложно только при , а в остальных случаях – истинно. Решение (комментарий к таблице)
- 35. Скачать презентацию





















 2_Calculations
2_Calculations Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Год, месяц, сутки
Год, месяц, сутки Применение мультимедийных презентаций для закрепления навыка оформления краткой записи задачи и её решения. Модуль 2
Применение мультимедийных презентаций для закрепления навыка оформления краткой записи задачи и её решения. Модуль 2 Презентация на тему Математический диктант
Презентация на тему Математический диктант  Квадратная матрица
Квадратная матрица Комбинаторика. Задача 1 (6 класс)
Комбинаторика. Задача 1 (6 класс) Оптимизация элементов треугольника при решении задачи Как поспорили Иван Иванович с Иваном Никифоровичем
Оптимизация элементов треугольника при решении задачи Как поспорили Иван Иванович с Иваном Никифоровичем Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Теория вероятностей. Системы случайных величин
Теория вероятностей. Системы случайных величин Подобные слагаемые. 7 класс
Подобные слагаемые. 7 класс Презентация на тему Математические диктанты 3 класс
Презентация на тему Математические диктанты 3 класс  Задачи на части
Задачи на части Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12
Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12 определение и свойства числ.функции
определение и свойства числ.функции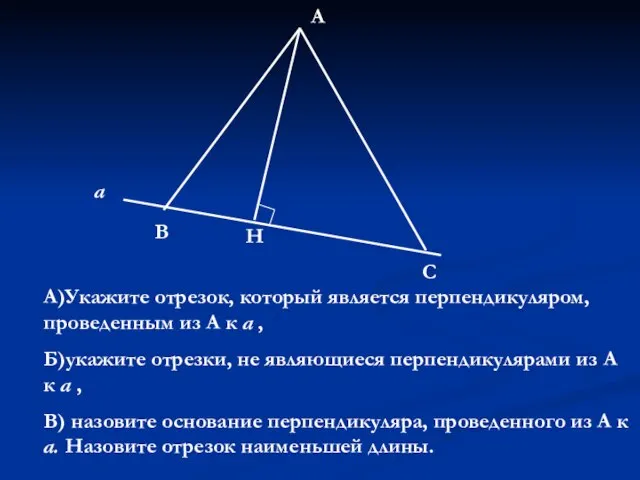 Построение треугольника
Построение треугольника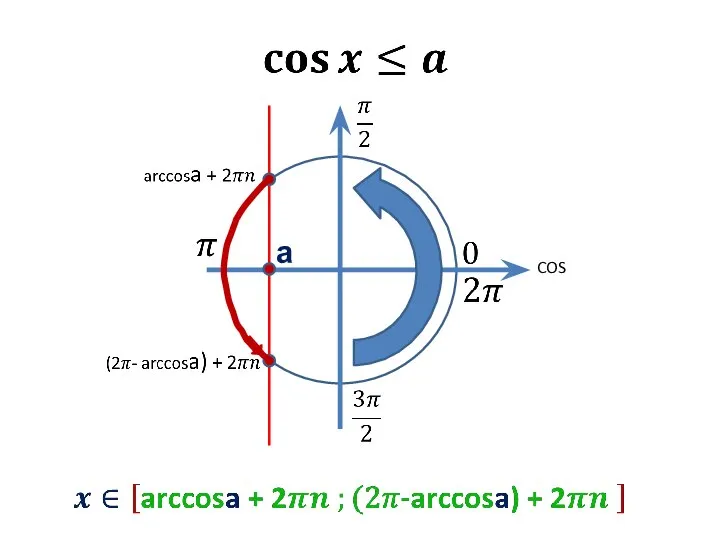 Неравенства вида Cos〖x≤a〗
Неравенства вида Cos〖x≤a〗 Корреляционный анализ в Exel
Корреляционный анализ в Exel Числові нерівності. Властивості числових нерівностей
Числові нерівності. Властивості числових нерівностей Арксинус и уравнение вида sinx=a
Арксинус и уравнение вида sinx=a Разложение вектора
Разложение вектора Математическое и сенсорное развитие детей раннего возраста
Математическое и сенсорное развитие детей раннего возраста Прямоугольник. Периметр прямоугольника
Прямоугольник. Периметр прямоугольника Методика изучения площади
Методика изучения площади Математический диктант
Математический диктант Как не забыть математику за лето советы методиста
Как не забыть математику за лето советы методиста Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8
Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8 Решение примеров
Решение примеров