Неполное квадратное уравнение

Проверка домашнего задания:
№ 231(а,б)
№ 232(а,б)
х = 0
х = 0
х1 = 0, х2 = 2
х1 = 0, х2 = -4

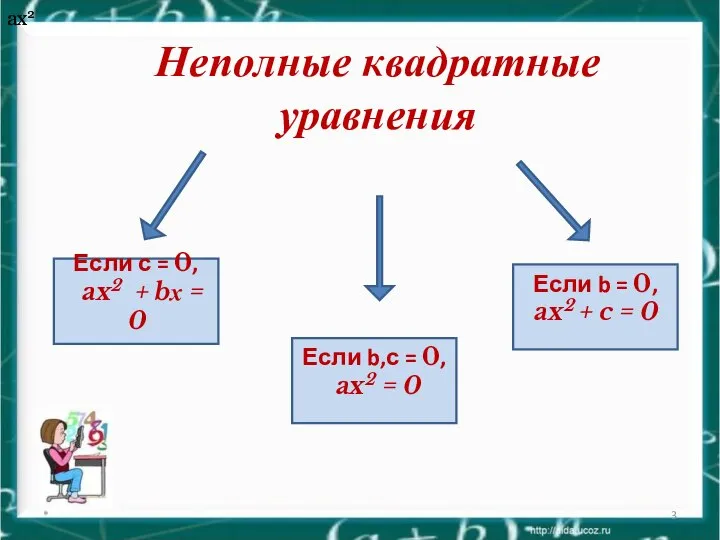
Неполные квадратные
уравнения
*
Если с = 0,
ax2 + bх = 0
ax2
ax2
Если b,с = 0,
ax2 = 0
Если b = 0,
ax2 + c = 0

Рассмотрим все возможные случаи

Неполные квадратные уравнения вида:

Неполные квадратные уравнения вида:
нет корней.

Неполные квадратные уравнения вида:

Запишите квадратные уравнения с указанными коэффициентами:
Установите соответствие между уравнениями и следующими
а) уравнение имеет два корня,
б) уравнение имеет один корень,
в) уравнение не имеет корней.
(в)
(а)
(б)
(а)
(а)
(а)
Установите соответствие между уравнениями и следующими утверждениями:

Решите уравнения:
а) 4х2 - 9 =0 в) -0,1х2 + 10 = 0 г) 6у2 + 24=0

Проверьте решение уравнений:
а) 4х2-9=0 в) -0,1х2+10=0 г) 6у2+24=0
4х2 =9 -0,1х2 =-10 6у2 =-24
х2 =9/4 х2 =-10:(-0,1) у2 =-24/6
х1= -3/2=-1,5; х2=100 у2 = - 4
х2 =3/2=1,5; х1= -10, х2= 10 Ответ: нет корней
Ответ:-1,5;1,5 Ответ:-10;10

*
Решите уравнения:
б) -5х2+ 6х=0 г) 4а2 – 3а=0 д) 6z2– z =0
.

*
Проверьте решение уравнений:
б) -5х2+ 6х=0 г) 4а2 - 3а=0 д) 6z2– z =0
х(-5х+6)=0 а(4а-3)=0 z(6z –1) =0 х=0 или -5х+6=0 а=0 или 4а-3=0 z=0 или 6z –1 =0
-5х= -6 4а=3 6z=1
х = -6/(-5) =1,2 а=3/4=0,75 z=1/6
Ответ: 0; 1,2. Ответ: 0; 0,75. Ответ: 0; 1/6..
.

*

Нет решений
2) При каких значениях a уравнение является неполным квадратным уравнением ?

Ответ: 1) при а = −2, х1= −15, х2=0;
2) при а = 0,