Слайд 2
Операцию нахождения для функции y = f(x) её производной функции называют дифференцированием функции

f(x).
Слайд 3 Правила дифференцирования
1) Производная постоянной функции равна нулю, т.е.
C ′ = 0, где С –

константа.
2) Производная суммы (разности) равна сумме (разности) производных, т.е.
Производная произведения находится по правилу:
Замечание. Формула дифференцирования произведения может быть легко обобщена на случай большего числа множителей. Например,
Слайд 4 , где С – константа.
Говорят: «постоянный множитель выносится за знак

производной».
5) Производная дроби находится по правилу:
6) Если функция ϕ(t) имеет производную в точке t, а функция f(u) имеет производную в точке u = ϕ(t), то сложная функция y = f(ϕ(t)) имеет производную в точке t, причем
(правило дифференцирования сложной функции).
Слайд 5УПРАЖНЕНИЯ.
1) Зная, что (sinx) ′ = cosx, (cosx) ′ = –sinx, (ex) ′ = ex, получить формулы
2)





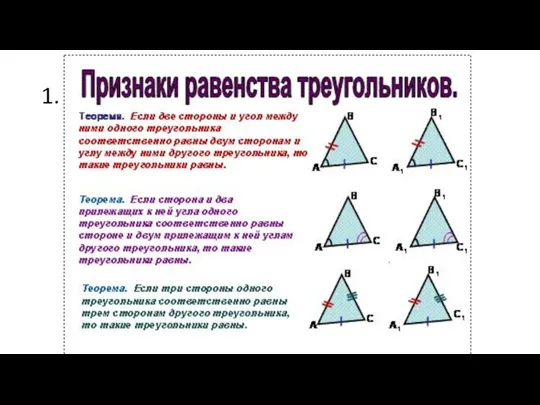 Признаки равенства треугольников
Признаки равенства треугольников Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Умножение обыкновенных дробей
Умножение обыкновенных дробей TA&Ml_ukr_1
TA&Ml_ukr_1 Инженерно-вычислительные технологии
Инженерно-вычислительные технологии Применение производной к исследованию функции
Применение производной к исследованию функции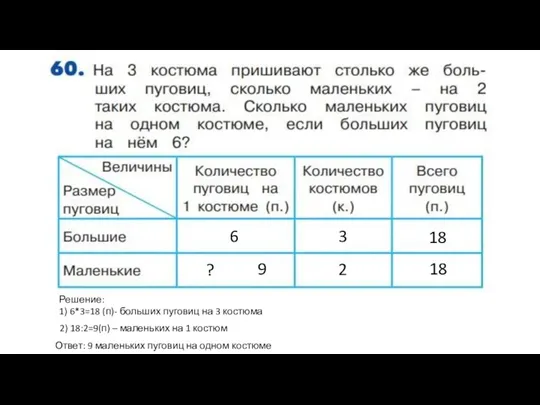 Задача о костюмах
Задача о костюмах Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Дискретные случайные величины
Дискретные случайные величины Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Критерий линейной корреляции Пирсона
Критерий линейной корреляции Пирсона Построение сечений
Построение сечений Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным Золотое сечение в архитектуре, скульптуре, живописи
Золотое сечение в архитектуре, скульптуре, живописи Задачи на построение
Задачи на построение Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)
Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)  Равносильные уравнения и неравенства
Равносильные уравнения и неравенства Компланарные векторы
Компланарные векторы Цветочное настроение (порядковый счет)
Цветочное настроение (порядковый счет) Венегрет. Урок
Венегрет. Урок Презентация по математике "Портреты учёных математиков" -
Презентация по математике "Портреты учёных математиков" -  График функций. Домашняя работа по алгебре
График функций. Домашняя работа по алгебре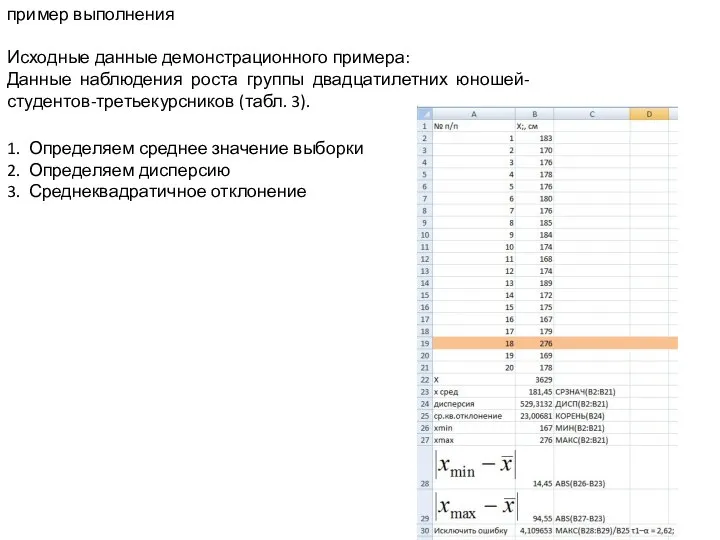 Данные наблюдения роста группы двадцатилетних юношей студентов
Данные наблюдения роста группы двадцатилетних юношей студентов Ломаная линия
Ломаная линия Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс