Слайд 2Теория моделей — раздел математической логики, который занимается изучением связи между формальными

языками и их интерпретациями, или моделями. Название теория моделей было впервые предложено Альфредом Тарским в 1954 году. Основное развитие теория моделей получила в работах Тарского, Мальцева и Робинсона.
Слайд 3Форма́льный язы́к в математической логике, информатике и лингвистике — множество конечных слов

(строк, цепочек) над конечным алфавитом. Понятие языка чаще всего используется в теории автоматов, теории вычислимости и теории алгоритмов. Научная теория, которая имеет дело с этим объектом, называется теорией формальных языков.
В теории моделей язык строится из множеств символов, функций и отношений вместе с их арностью, а также множества переменных. Каждое из этих множеств может быть бесконечным. Из языка вместе с универсальными логическими символами составляются логические высказывания.
Слайд 4Классическая теория моделей первого порядка
Теория моделей для классической логики первого порядка является

исторически первым и наиболее развитым примером теоретико-модельного подхода. В роли моделей здесь выступают множества, представляющие область возможных значений переменных. Функциональные символы интерпретируются как операции соответствующей арности над ними, а предикаты — как отношения (более подробно, см. Логика первого порядка, интерпретация).
Слайд 5Логика первого порядка — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций

и предикатов. Расширяет логику высказываний.
Помимо логики первого порядка существуют также логики высших порядков, в которых кванторы могут применяться не только к переменным, но и к множествам. Термины логика предикатов и исчисление предикатов могут означать как логику первого порядка, так и логики первого и высшего порядка вместе; в первом случае иногда говорится о чистой логике предикатов или чистом исчислении предикатов.




 Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Вавилонская математика
Вавилонская математика Математическая шарада
Математическая шарада Китайская математика
Китайская математика Порядок действий в вычислениях
Порядок действий в вычислениях Алгебраические действия над комплексными числами
Алгебраические действия над комплексными числами Тема 1
Тема 1 Проценты. Готовимся к ОГЭ
Проценты. Готовимся к ОГЭ Состав числа 8
Состав числа 8 Презентация на тему Предел переменной величины
Презентация на тему Предел переменной величины  Производная функции. Обобщающий урок
Производная функции. Обобщающий урок Построение графиков функций с помощью производных
Построение графиков функций с помощью производных Сравнение натуральных чисел
Сравнение натуральных чисел Величины, длина
Величины, длина Нахождение sin и tg
Нахождение sin и tg Сложение с переходом через десяток вида +2, +3, +4, +5. Считаем с гномами
Сложение с переходом через десяток вида +2, +3, +4, +5. Считаем с гномами Проценты
Проценты Методы решения систем линейных уравнений: метод сложения
Методы решения систем линейных уравнений: метод сложения Координатная плоскость
Координатная плоскость От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Интеграл, интеграция, интегрирование. Решение задач
Интеграл, интеграция, интегрирование. Решение задач Переместительное свойство умножения
Переместительное свойство умножения ЕГЭ по математике. Экономические задачи VII
ЕГЭ по математике. Экономические задачи VII Тема урока: Умножение чисел на сумму
Тема урока: Умножение чисел на сумму Многоугольники и многогранники в архитектуре и живописи
Многоугольники и многогранники в архитектуре и живописи Замена числа суммой разрядных слагаемых. (дистанционное обучение)
Замена числа суммой разрядных слагаемых. (дистанционное обучение)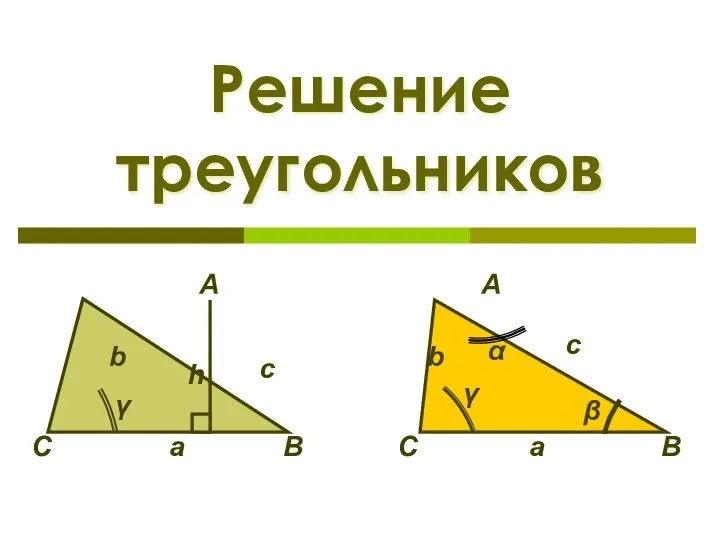 Решение треугольников
Решение треугольников Блестящая Математика: Математические Игры С Камешками марблс
Блестящая Математика: Математические Игры С Камешками марблс