Решение систем неравенств (9 класс)

Математику нельзя изучать, наблюдая как это делает сосед.
А. Нивен

Запомним
Решить систему неравенств – это значит найти значение переменной, при котором верно каждое из неравенств системы.

Запомним
Если надо решить систему неравенств, то:
решаем каждое неравенство системы отдельно
изображаем полученные решения на числовой прямой и смотрим пересечения этих решений.
Эта общая часть и является решением данной системы неравенств.

Содержание
Решение систем линейных неравенств
Решение двойных неравенств
Решение систем, содержащих квадратные неравенства

Решим систему неравенств
(состоящую из линейных неравенств)
5х + 1 > 6
2х – 4 < 3
Решение: решим каждое неравенство отдельно
5х + 1 > 6 2х – 4 < 3
5х > 6 -1 2х < 4+3
5х > 5 2х < 7
х >1 х < 3,5
1 3,5 х
Ответ: (1; 3,5)

Решим систему неравенств
5х + 12 ≤ 3х+ 20
х < 2х+3 2х + 7 ≥ 0
Решение: решим каждое неравенство отдельно
5х + 12 ≤ 3х+ 20 х < 2х+3 2х + 7 ≥ 0
5х – 3х ≤ - 12 + 20 х – 2х < 3 2х ≥ -7
2х ≤ 8 -х < 3 х ≥ -7/2
х ≤ 4 х > - 3 х ≥ -3,5
Изобразим на числовой прямой:
-3,5 -3 4
Ответ: ( -3; 4]

Работа в парах:
Решить систему
неравенств:
1) 3х – 2 ≥ х + 1
4 – 2х ≤ х – 2
2) 3х > 12 + 11х
5х – 1 ≥ 0
Проверим ответы:
1) [2; +∞)
2) Нет решения

Примеры двойных неравенств
Прочитайте неравенства:
-6 < х < 0
-1,2 ≤ х < 3,5
0 < х ≤ 5,9

Решение двойных неравенств
Решить неравенство: 0< 4х +2 ≤ 6
Решение: составим систему: 4х + 2 > 0
4х + 2 ≤ 6
Решим каждое неравенство системы отдельно:
1) 4х + 2 > 0 2) 4х + 2 ≤ 6
х > - 0,5 х ≤ 1
Полученные результаты изобразим на числовой прямой:
-0,5 1 х
Ответ: -0,5 < х ≤ 1 или (-0,5; 1]

Решите неравенства,
работая в парах
Решить неравенства:
-6 ≤ - 3х ≤ 3
4 < 2х – 1 ≤ 13
-2 ≤ 6х + 7 < 1
0,3 < 0,5 + 0,1х < 0,6
0 < - 2х < 8
Проверим
ответы:
1) [-1; 2]
2) (2,5; 7]
3) [- 1,5; - 1)
4) (-2; 1)
5) (-4; 0)

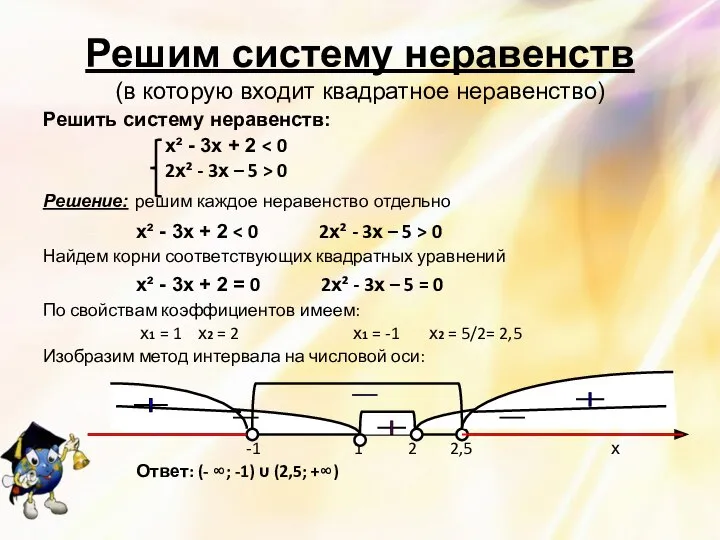
Решим систему неравенств
(в которую входит квадратное неравенство)
Решить систему неравенств: х² - 5х + 4 ≤ 0
9 - 4х < 0
Решение: решим каждое неравенство системы отдельно
1) х² - 5х + 4 ≤ 0 2) 9 - 4х < 0
х² - 5х + 4 = 0 - 4х < - 9
т.к. а+в+с=0, то х1=1; х2=4 х > 9/4=2,25
Полученные результаты изобразим на числовой прямой:
1 2,25 4 х
Ответ: [ 4; +∞)
+
-
-

Решить систему неравенств:
х² - 3х + 2 < 0
2х² - 3х – 5 > 0
Решение: решим каждое неравенство отдельно
х² - 3х + 2 < 0 2х² - 3х – 5 > 0
Найдем корни соответствующих квадратных уравнений
х² - 3х + 2 = 0 2х² - 3х – 5 = 0
По свойствам коэффициентов имеем:
х1 = 1 х2 = 2 х1 = -1 х2 = 5/2= 2,5
Изобразим метод интервала на числовой оси:
-1 1 2 2,5 х
Ответ: (- ∞; -1) υ (2,5; +∞)
Решим систему неравенств
(в которую входит квадратное неравенство)
+
+
+
-
-
-

Решим системы неравенств,
1) 6х² - 5х + 1 > 0
4х – 1 ≥ 0
2) 4х² - 1 ≤ 0
х² > 1
3х² - 2х – 1 < 0
х² - х – 6 > 0