Содержание
- 2. Цель занятия: изучение функциональных возможностей табличного процессора Excel 2007 и приобретение навыков практической работы по использованию
- 3. План лабораторного занятия: Добавление надстройки «Поиск решения» Постановка задачи линейного программирования 3. Решение задач 4. Задание
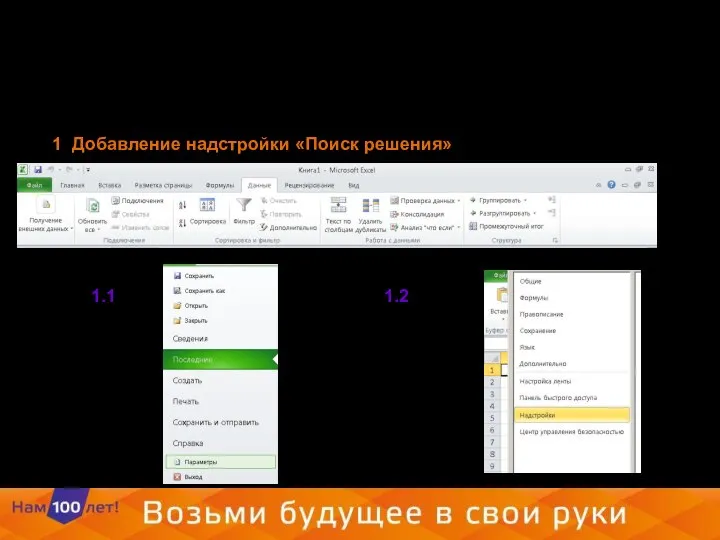
- 4. 1. Добавление надстройки «Поиск решения» 1.1 1.2
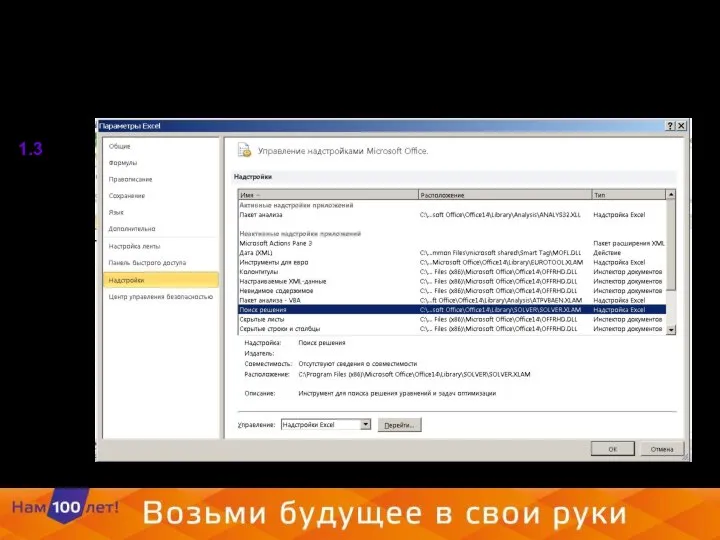
- 5. 1.3
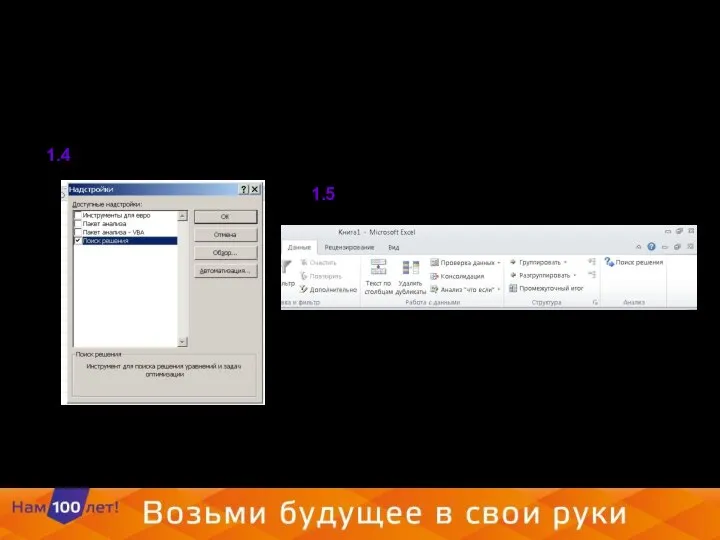
- 6. 1.4 1.5
- 7. Линейное программирование (ЛП) – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума
- 8. Задача распределения неоднородных ресурсов. Составление оптимального плана выпуска продукции Краткая теория Пусть некоторое предприятие обладает ресурсами
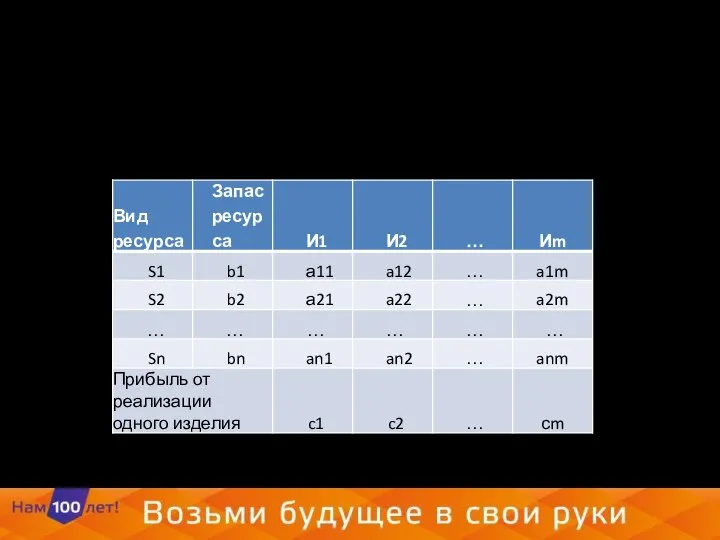
- 9. Для решения поставленной задачи сформулируем её математическую модель, первоначально сведя исходные данные в следующую таблицу:
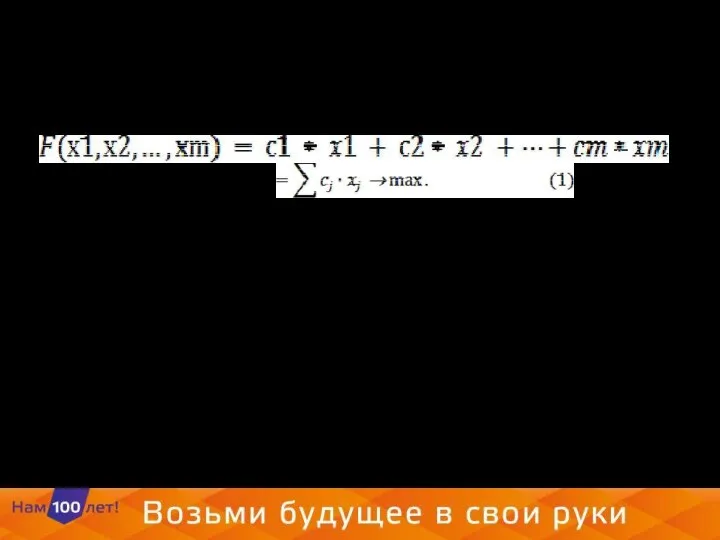
- 10. Математическая модель задачи распределения неоднородных ресурсов. Для построения математической модели задачи: 1. Определим неизвестные и их
- 11. Сформулируем ограничения рассматриваемой задачи. Ограничения по запасам сырья. Зная количество сырья каждого вида, идущее на изготовление
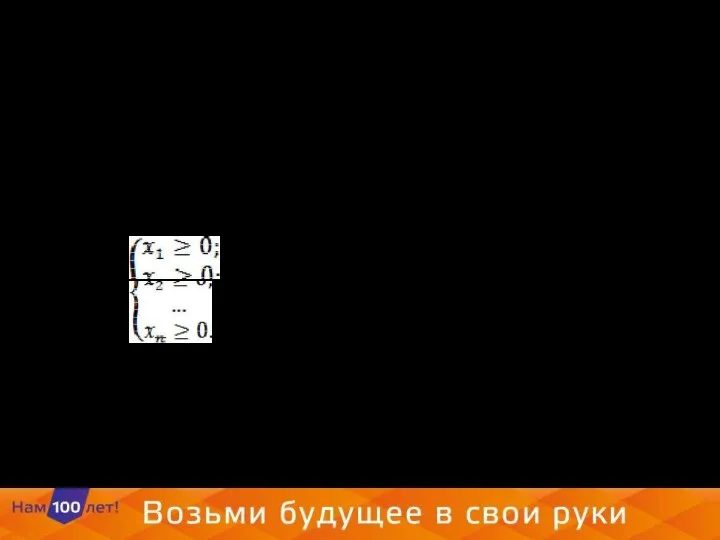
- 12. 3.2.Условие неотрицательности переменных. Исходя из физического смысла, на переменные налагаются дополнительные условия, требующие неотрицательности их значений:
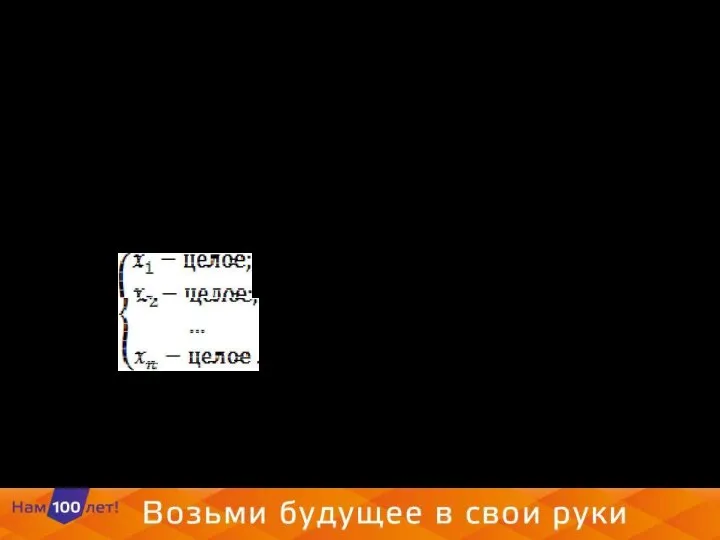
- 13. Условие целочисленности переменных. На переменные можно накладывать дополнительное условие целочисленности, которое “ запрещает” выпуск не целых
- 14. Пример Постановка задачи. Пусть предприятие располагает запасами сырья трех видов – цемент, щебень и арматура в
- 15. Направление подготовки бакалавров 38.03.06 Торговое дело профиль Коммерция Б2.В.ОД.1 Компьютерное моделирование в профессиональной деятельности Таблица 1.
- 16. Требуется составить такой план продукции, при котором прибыль была бы максимальной Математическая модель задачи распределения неоднородных
- 17. Ограничения по запасам сырья. Зная количество сырья каждого вида, идущее на изготовление одной единицы изделия, и
- 18. Условие неотрицательности переменных. Исходя из физического смысла, на переменные налагаются дополнительные условия, требующие неотрицательности их значений:
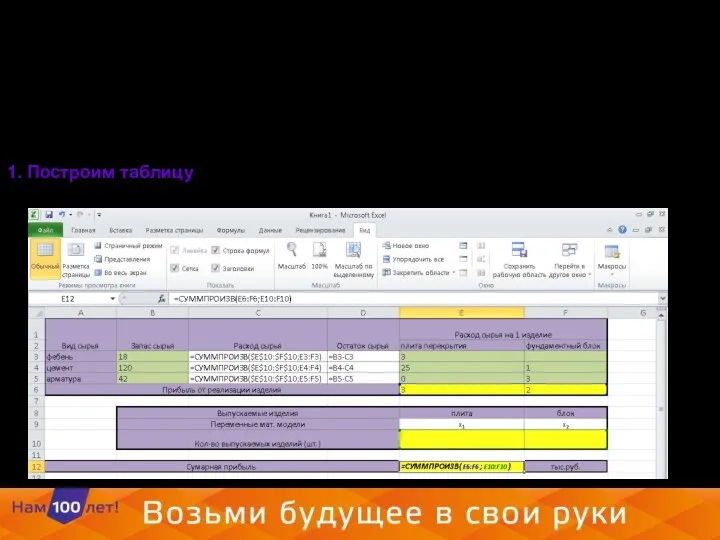
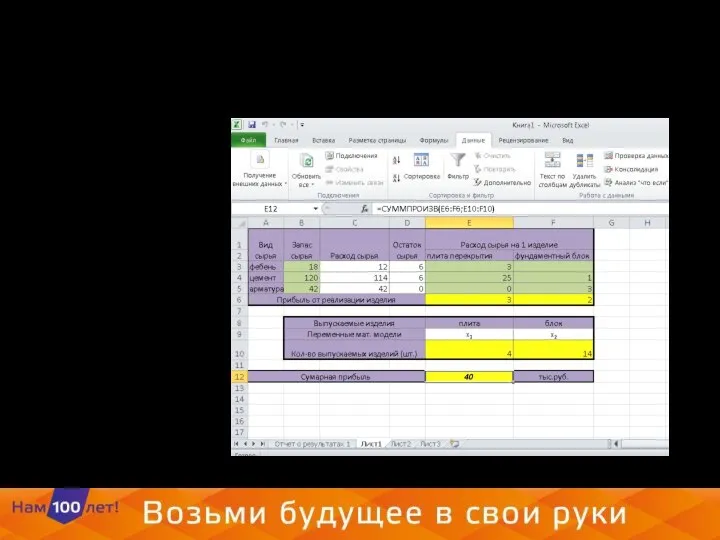
- 19. Решение задачи 1. Построим таблицу
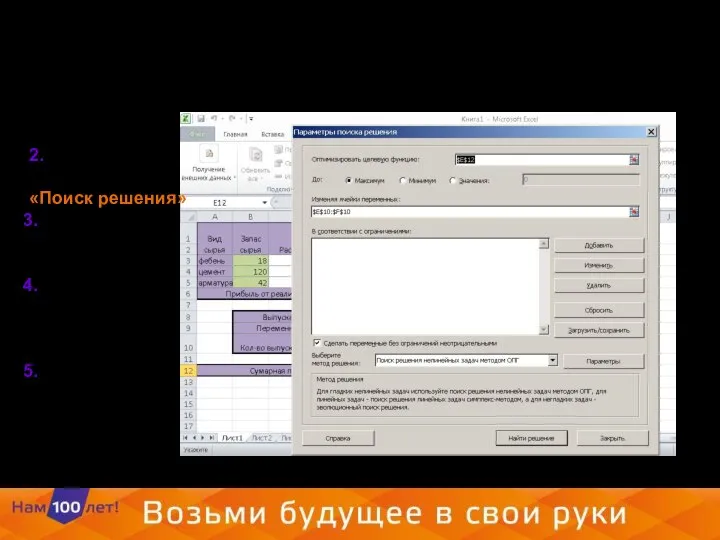
- 20. 2. Выберем на вкладке данные «Поиск решения» Зададим целевую функцию. Желаемое значение целевой функции Изменяемые ячейки
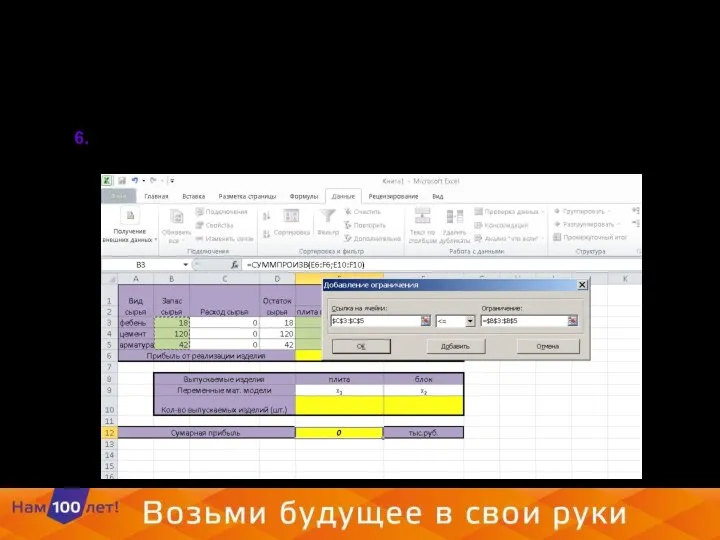
- 21. 6. Зададим ограничения по ресурсам
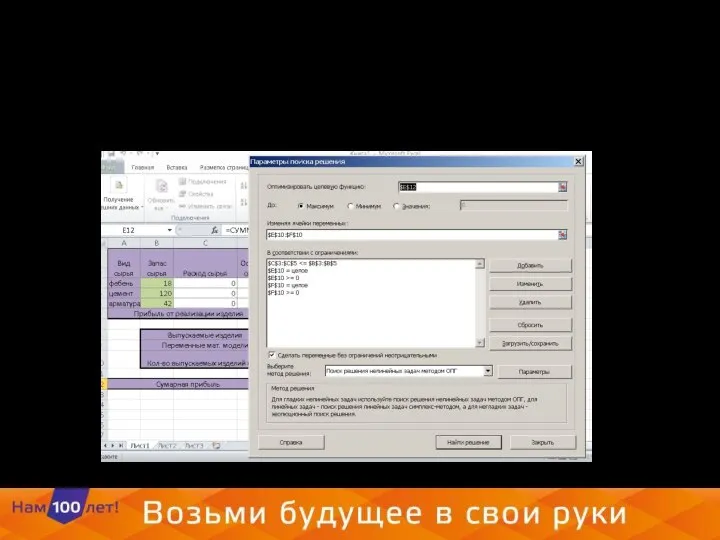
- 22. 7. Введем ограничения на выпуск продукции
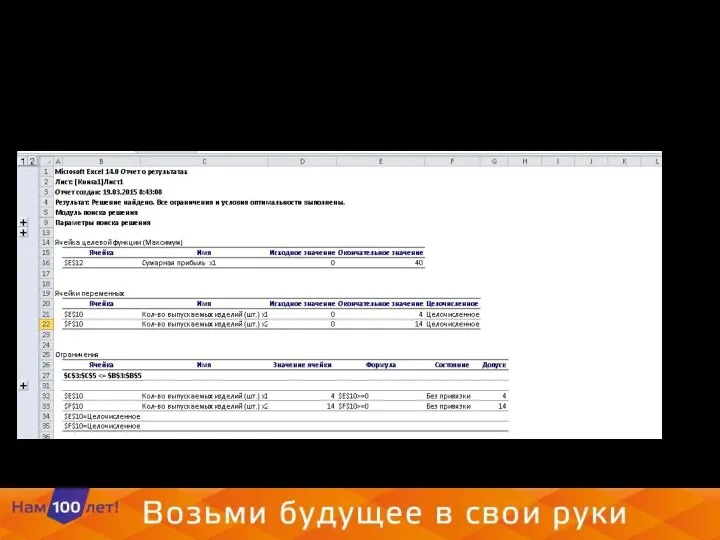
- 23. В результате получаем следующие дынные
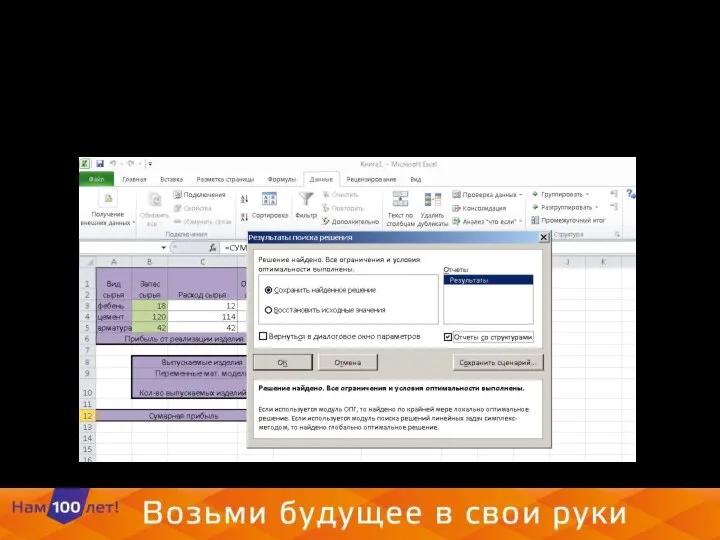
- 24. Сохраним отчеты
- 25. Результат решения
- 27. Направление подготовки бакалавров 38.03.06 Торговое дело профиль Коммерция Б2.В.ОД.1 Компьютерное моделирование в профессиональной деятельности
- 28. Направление подготовки бакалавров 38.03.06 Торговое дело профиль Коммерция Б2.В.ОД.1 Компьютерное моделирование в профессиональной деятельности
- 29. Направление подготовки бакалавров 38.03.06 Торговое дело профиль Коммерция Б2.В.ОД.1 Компьютерное моделирование в профессиональной деятельности
- 31. Скачать презентацию














 Анализ и изображение пространственных фигур
Анализ и изображение пространственных фигур Исследование функций
Исследование функций Скрипт параллелограм
Скрипт параллелограм Презентация на тему Параллельный перенос и Поворот
Презентация на тему Параллельный перенос и Поворот  Математик Чарльз Лютвидж Доджсон и писатель Льюис Кэрролл
Математик Чарльз Лютвидж Доджсон и писатель Льюис Кэрролл Сложение вида +6
Сложение вида +6 Письменные приемы вычислений
Письменные приемы вычислений Сказка об отрезке
Сказка об отрезке Деление десятичных дробей
Деление десятичных дробей Разложение вектора по направлениям. Скалярное произведение векторов
Разложение вектора по направлениям. Скалярное произведение векторов Особенности проведения олимпиады по математике в 2016-17 учебном году
Особенности проведения олимпиады по математике в 2016-17 учебном году Многогранники в нашей жизни
Многогранники в нашей жизни Презентация на тему Квадратичная функция и ее свойства
Презентация на тему Квадратичная функция и ее свойства  Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Дроби
Дроби Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Пропорция
Пропорция Таблица умножения на 2
Таблица умножения на 2 Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Вопросы при решении задач
Вопросы при решении задач Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы
Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы Презентация на тему Приемы доказательства неравенств, содержащих переменные
Презентация на тему Приемы доказательства неравенств, содержащих переменные  Параллельные прямые
Параллельные прямые Страна геометрических фигур
Страна геометрических фигур Исследование модели многогранника с сечениями на примере куба
Исследование модели многогранника с сечениями на примере куба Выборочное наблюдение
Выборочное наблюдение Игра на поиск логических пар
Игра на поиск логических пар Действия с десятичными дробями. 5 класс
Действия с десятичными дробями. 5 класс