Содержание
- 2. Рассмотрим функцию y=f(x) ∆x – приращение аргумента; ∆y – приращение функции ∆y=f(x+ ∆x)-f(x) x y 0
- 3. Геометрический смысл производной Производная, найденная в точке x0 равна углу наклона касательной с положительным направлением оси
- 4. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Производная константы C - константа Производная суммы равна сумме производных Производная разности равна
- 5. 1. 2. 3. 4. 5. 6. 7. 8. ТАБЛИЦА ПРОИЗВОДНЫХ
- 6. 9. 10. 11. 12. 13.
- 7. u=f[g(x)] Производная сложной функции
- 9. Производной второго порядка называется производная от первой производной. Производной третьего порядка называется производная от второй производной.
- 11. Скачать презентацию





![u=f[g(x)] Производная сложной функции](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1028925/slide-6.jpg)
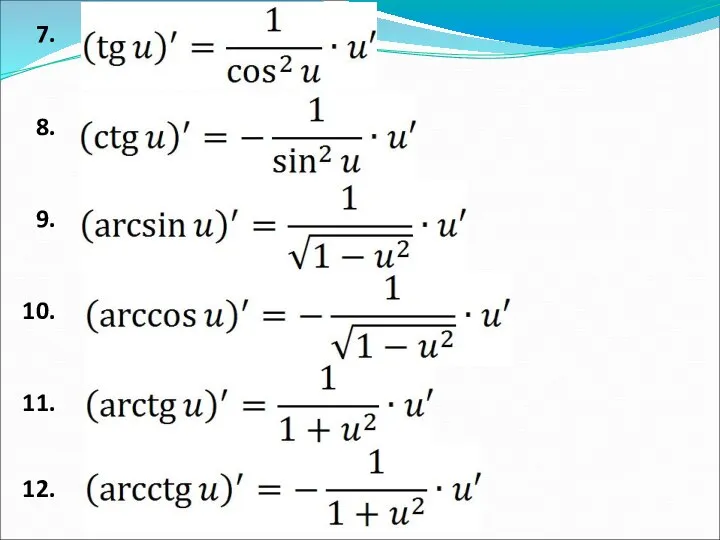

 Нечеткие отношения и их свойства
Нечеткие отношения и их свойства Случаи сложения и вычитания, основанные на знаниях нумерации
Случаи сложения и вычитания, основанные на знаниях нумерации Математические головоломки
Математические головоломки Матрицы
Матрицы Иррациональные уравнения. Основы школьного курса математики
Иррациональные уравнения. Основы школьного курса математики Обыкновенные дроби
Обыкновенные дроби Презентация на тему Деление десятичной дроби на натуральное число
Презентация на тему Деление десятичной дроби на натуральное число  Задачи на пропорциональное деление
Задачи на пропорциональное деление Степенные функции, их свойства и графики
Степенные функции, их свойства и графики Аксиомы планиметрии (часть 1)
Аксиомы планиметрии (часть 1) Сложная функция. Производная сложной функции
Сложная функция. Производная сложной функции Презентация на тему Преобразование целого выражения в многочлен
Презентация на тему Преобразование целого выражения в многочлен  Формула Бернулли
Формула Бернулли Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Веселое путешествие
Веселое путешествие Преобразование выражения A sin x + B cos х к виду С sin(x+t)
Преобразование выражения A sin x + B cos х к виду С sin(x+t) Комбинаторная задача с шарами
Комбинаторная задача с шарами Пирамида
Пирамида Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Исследование функции при помощи производной
Исследование функции при помощи производной Определение времени регулирования АС по переходной функции
Определение времени регулирования АС по переходной функции Тригонометрические функции и их свойства
Тригонометрические функции и их свойства Показательная функция, её свойства и график
Показательная функция, её свойства и график Презентация4. МСиТИ
Презентация4. МСиТИ Сложение до 20. Тренажер по математике. 2 класс
Сложение до 20. Тренажер по математике. 2 класс Занимательная математика
Занимательная математика Презентация на тему Табличное решение логических задач (7 класс)
Презентация на тему Табличное решение логических задач (7 класс)