Содержание
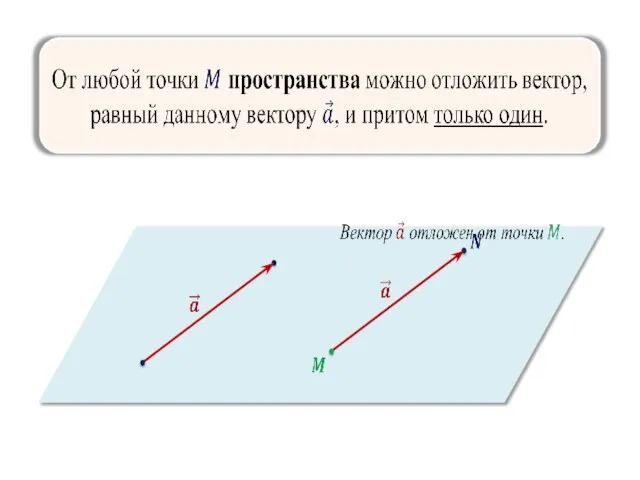
- 2. Вектор — направленный отрезок нулевой вектор Длина ненулевого вектора равна длине отрезка Длина нулевого вектора равна
- 3. Коллинеарные векторы — ненулевые векторы, лежащие на одной прямой или на параллельных прямых Нулевой вектор коллинеарен
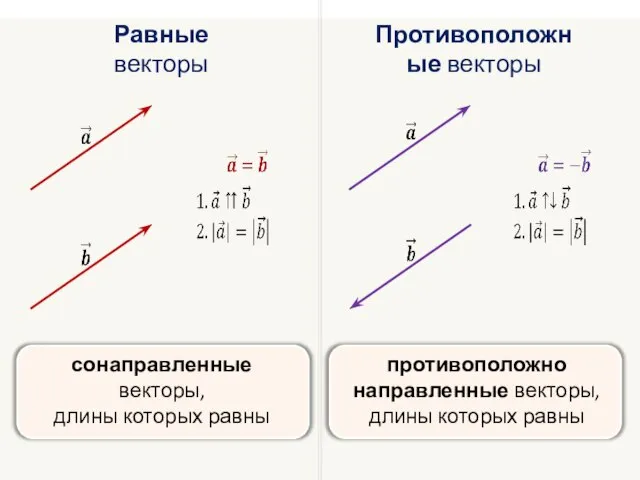
- 4. Равные векторы Противоположные векторы сонаправленные векторы, длины которых равны противоположно направленные векторы, длины которых равны
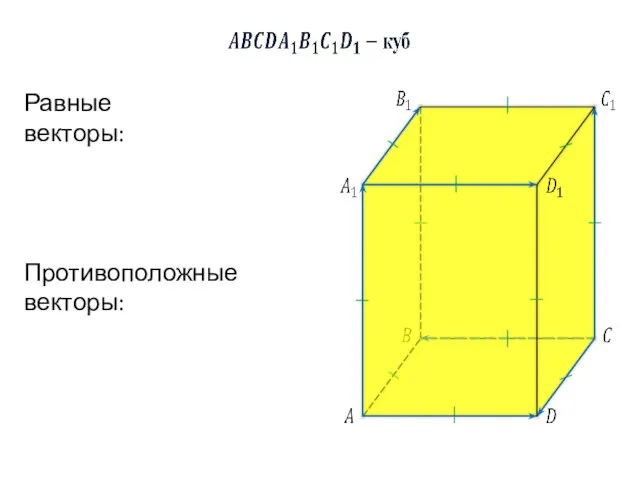
- 5. Равные векторы: Противоположные векторы:
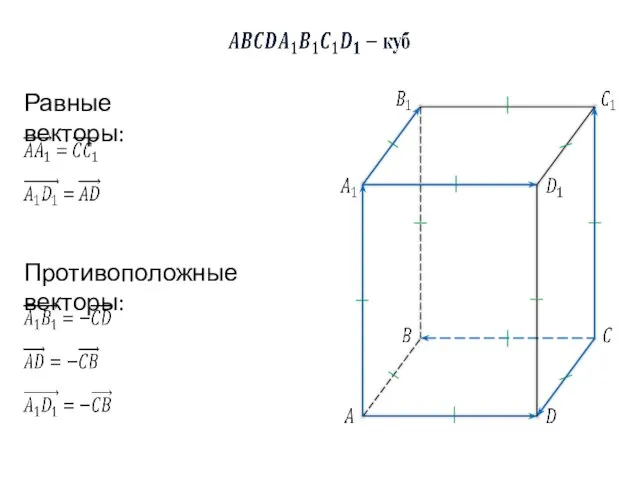
- 6. Равные векторы: Противоположные векторы:
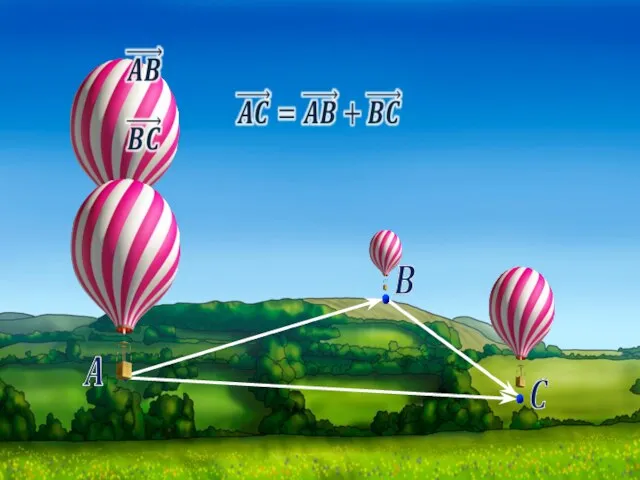
- 9. Сложение и вычитание векторов
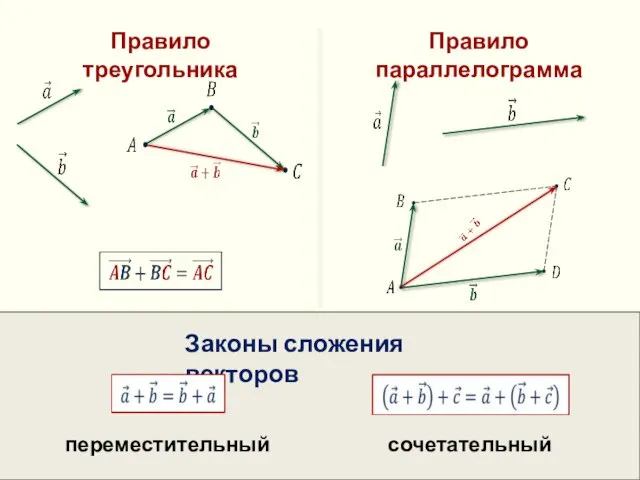
- 11. Правило треугольника
- 12. Правило треугольника Правило параллелограмма Законы сложения векторов переместительный сочетательный
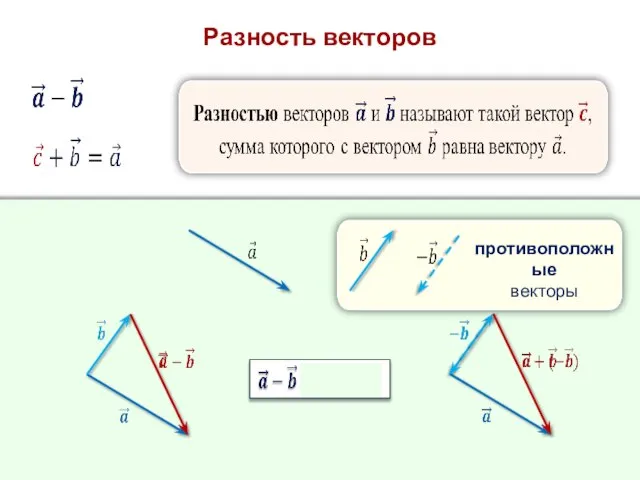
- 13. Разность векторов противоположные векторы
- 14. Сумма нескольких векторов
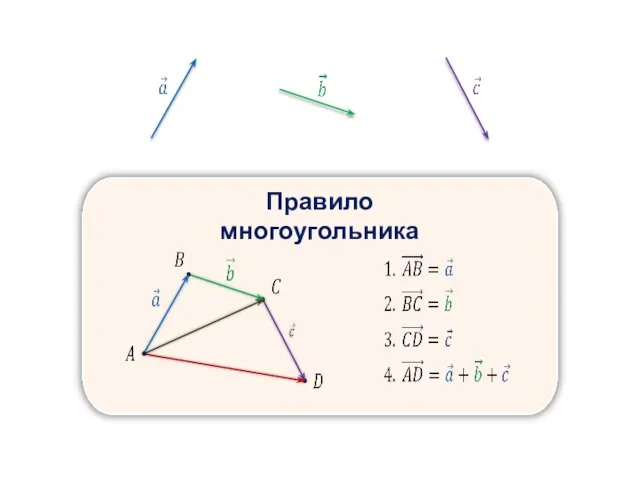
- 15. Правило многоугольника
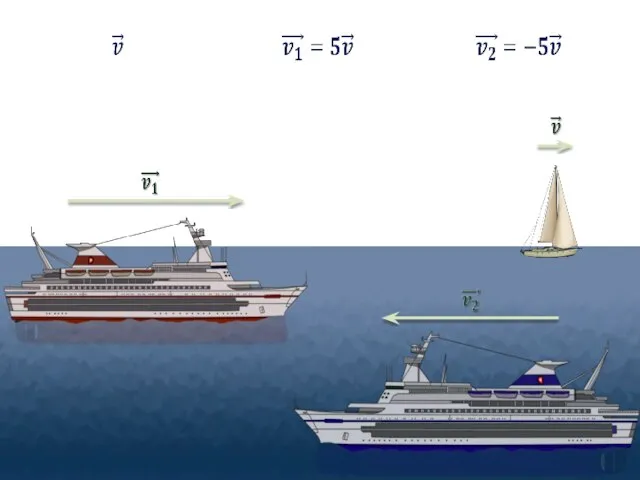
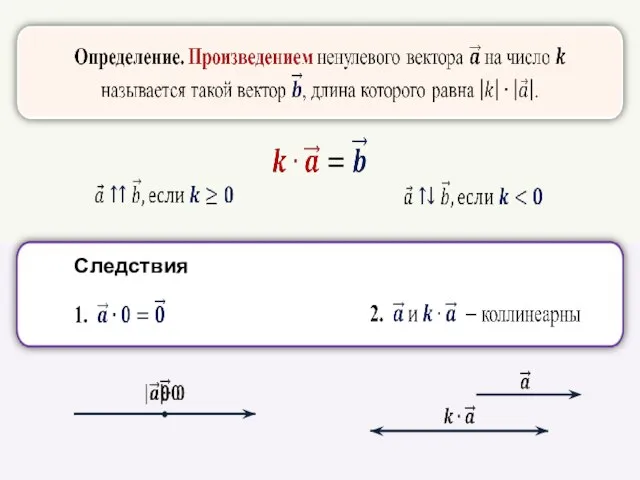
- 16. Умножение вектора на число
- 18. Следствия
- 19. Свойства произведения вектора на число позволяют выполнять преобразования в выражениях, содержащих суммы, разности векторов и произведения
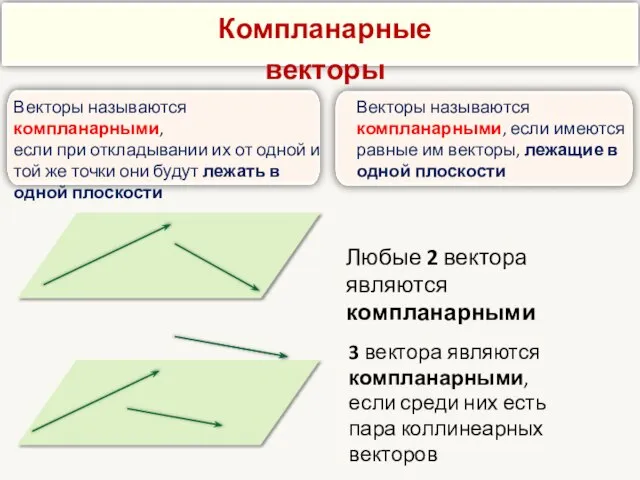
- 20. Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать
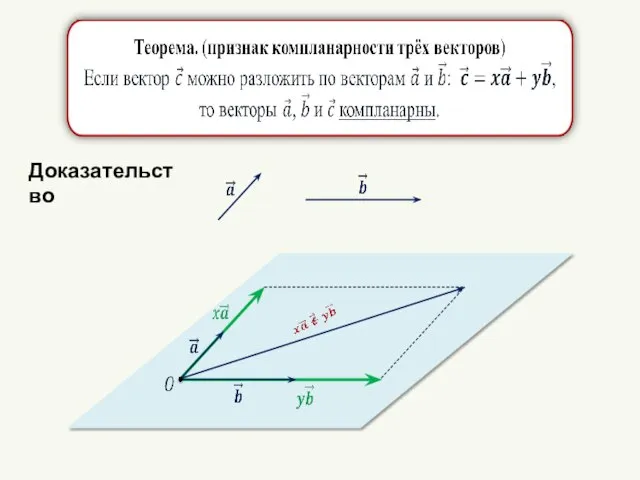
- 21. Доказательство
- 22. Доказательство.
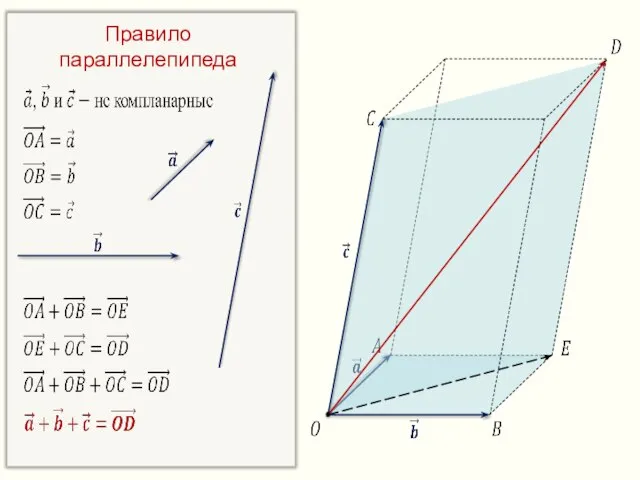
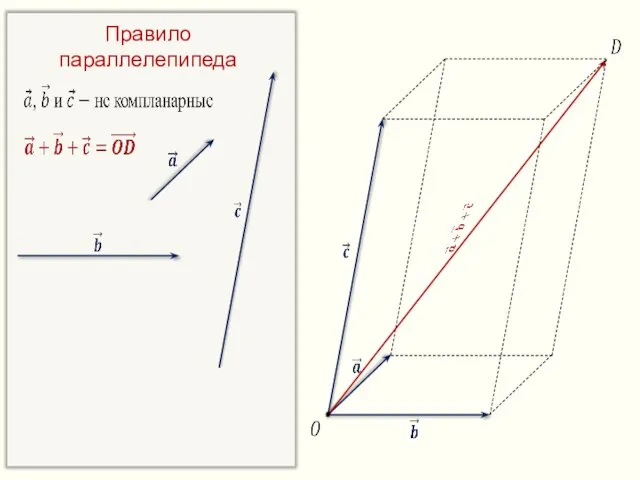
- 23. Правило параллелепипеда
- 24. Правило параллелепипеда
- 25. Правило параллелепипеда
- 26. Разложение вектора по трём некомпланарным векторам
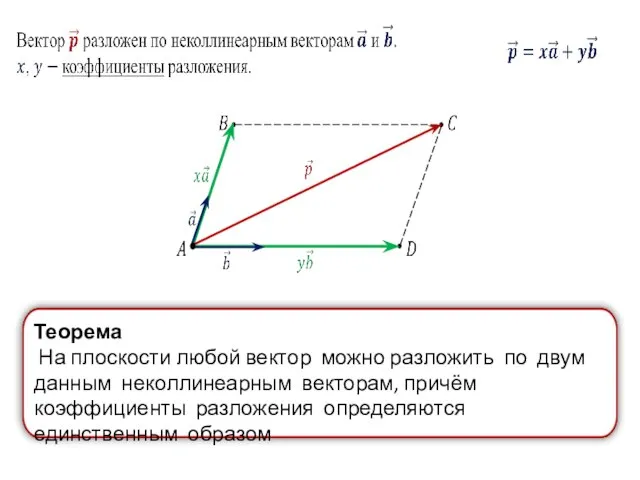
- 27. Теорема На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются
- 28. Прямоугольная система координат в пространстве
- 29. Рене Декарт 1596 - 1650 Французский философ, математик, механик, физик и физиолог Создатель аналитической геометрии и
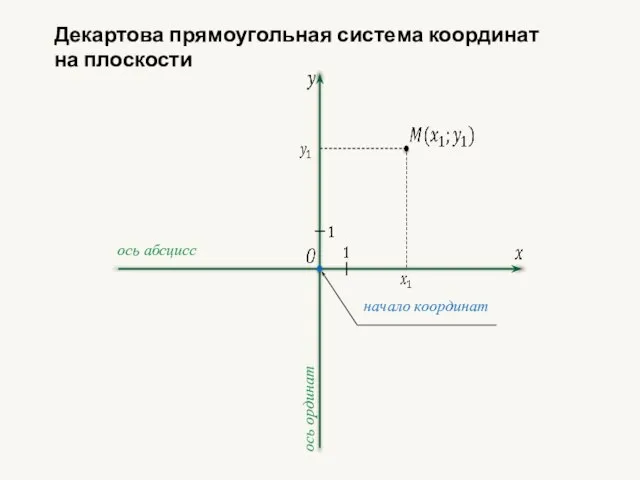
- 30. ось абсцисс ось ординат начало координат Декартова прямоугольная система координат на плоскости
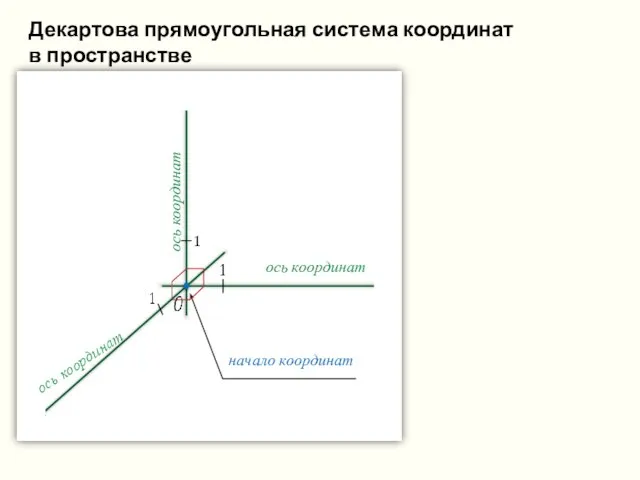
- 31. ось координат ось координат начало координат ось координат Декартова прямоугольная система координат в пространстве
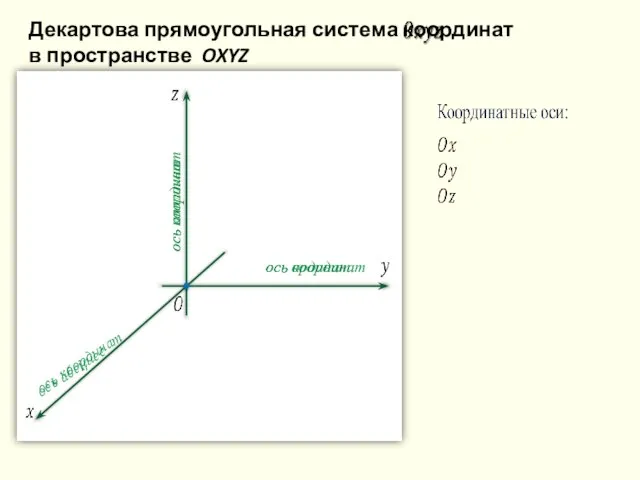
- 32. ось абсцисс ось ординат ось аппликат ось координат ось координат ось координат Декартова прямоугольная система координат
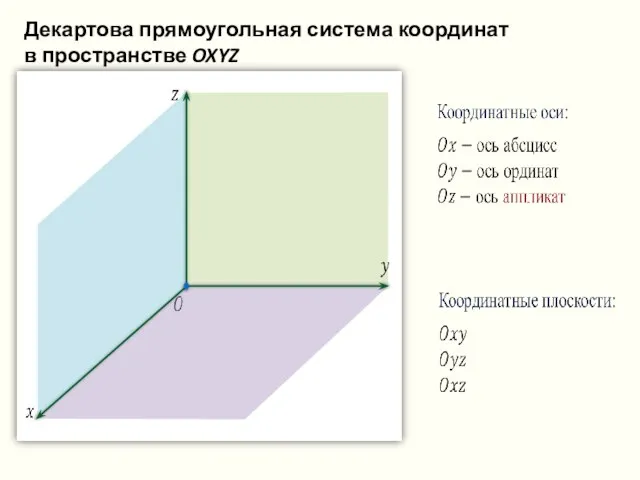
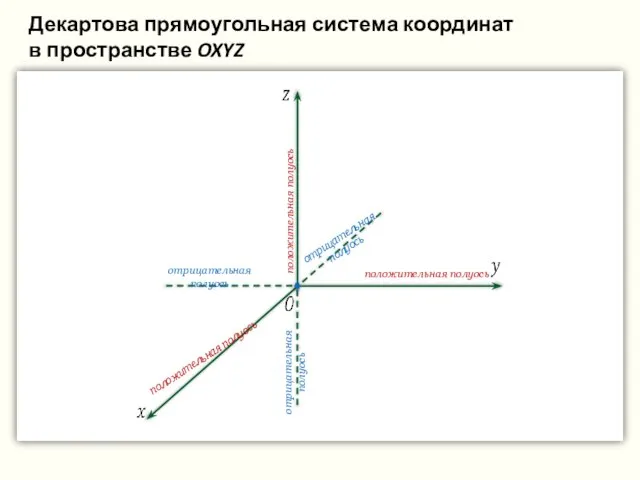
- 33. Декартова прямоугольная система координат в пространстве OXYZ
- 34. положительная полуось положительная полуось положительная полуось отрицательная полуось отрицательная полуось отрицательная полуось Декартова прямоугольная система координат
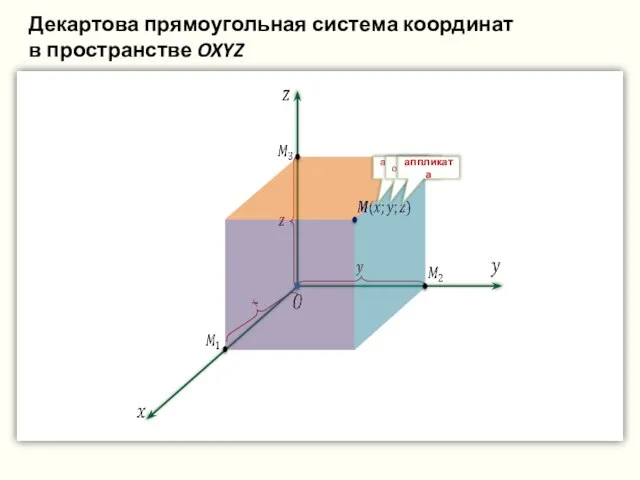
- 35. абсцисса ордината аппликата Декартова прямоугольная система координат в пространстве OXYZ
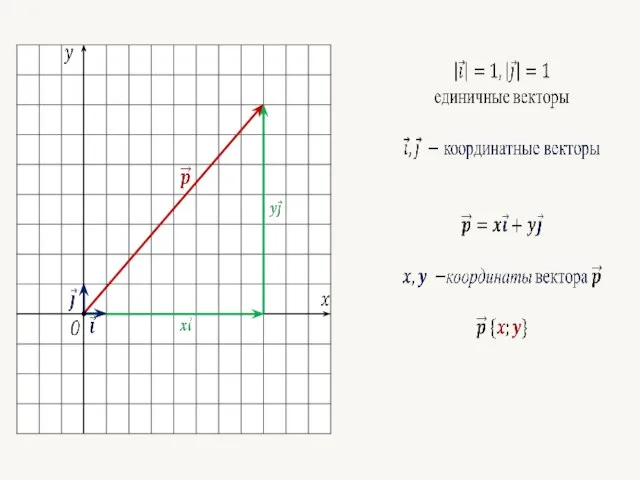
- 36. Координаты вектора
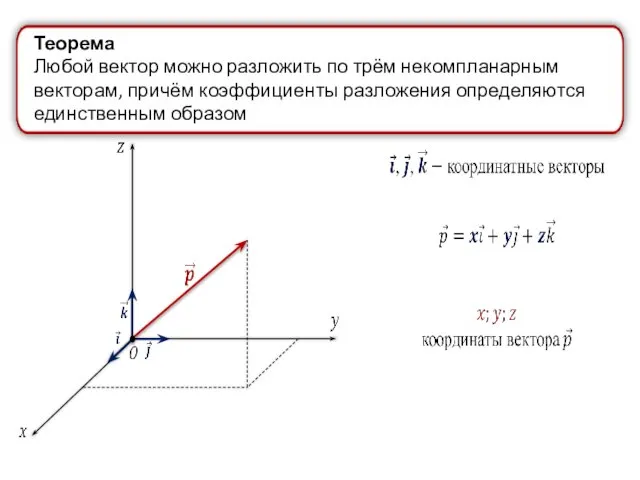
- 38. Теорема Любой вектор можно разложить по трём некомпланарным векторам, причём коэффициенты разложения определяются единственным образом
- 39. Пользуясь разложениями векторов по координатным векторам, записать их координаты Пользуясь координатами векторов, запишем их разложения по
- 40. Позволяют определять координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами
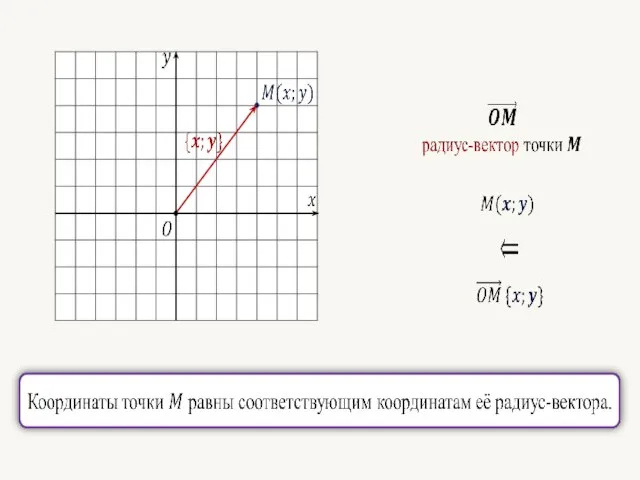
- 41. Связь между координатами векторов и координатами точек
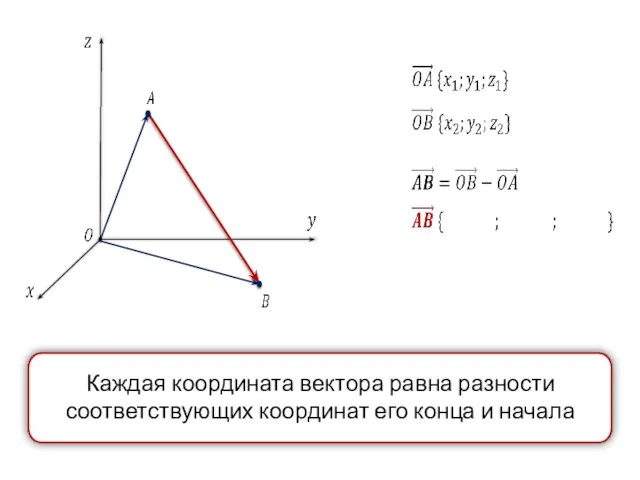
- 43. Каждая координата вектора равна разности соответствующих координат его конца и начала
- 44. Простейшие задачи в координатах
- 45. 1. Определение координат середины отрезка Каждая координата середины отрезка равна полусумме соответствующих координат его концов
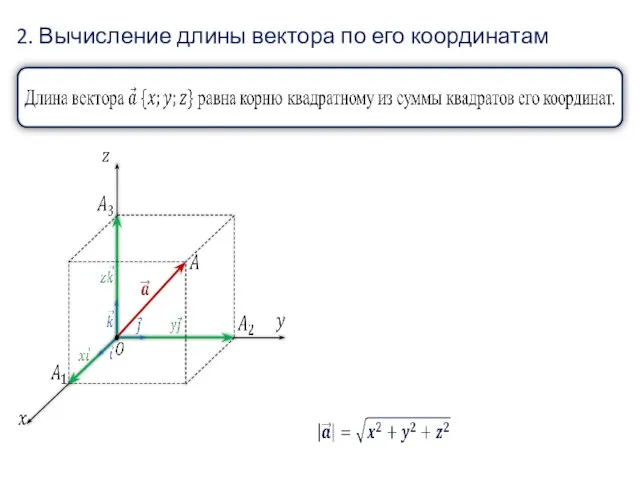
- 46. 2. Вычисление длины вектора по его координатам
- 47. Решение.
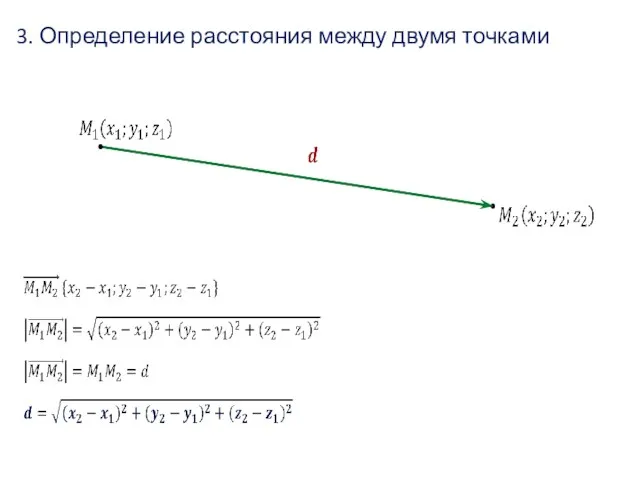
- 48. 3. Определение расстояния между двумя точками
- 49. Скалярное произведение векторов
- 50. Скалярное произведение двух векторов − произведение их длин на косинус угла между ними
- 51. Скалярное произведение векторов в координатах
- 52. Скалярное произведение векторов в координатах v v v v v v v v v v v
- 55. Скачать презентацию























 Площадь четырёхугольника
Площадь четырёхугольника Путешествие в страну Математику
Путешествие в страну Математику Теория вероятностей
Теория вероятностей Равносильность уравнений на множествах
Равносильность уравнений на множествах Числовое и буквенное выражения
Числовое и буквенное выражения Знакомство с монетами достоинством 1, 2, 5, 10 рублей
Знакомство с монетами достоинством 1, 2, 5, 10 рублей Общая математическая модель динамики
Общая математическая модель динамики Прямоугольный параллелепипед
Прямоугольный параллелепипед Случаи сложения вида +5
Случаи сложения вида +5 Площади фигур. 8 класс
Площади фигур. 8 класс Построение графиков функций с помощью геометрических преобразований
Построение графиков функций с помощью геометрических преобразований Площади многоугольников
Площади многоугольников Виды углов. Равные углы. Измерение углов. Задачи
Виды углов. Равные углы. Измерение углов. Задачи Исследование функции с помощью производной
Исследование функции с помощью производной Памятник числу π в Сиэтле
Памятник числу π в Сиэтле Бутылка Клейна
Бутылка Клейна Площадь фигур
Площадь фигур Уравнение вида ах2 + bx + c = 0,
Уравнение вида ах2 + bx + c = 0, Дроби. Задачи
Дроби. Задачи Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим
Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим Представление информации. Решение задач на проценты
Представление информации. Решение задач на проценты Названия чисел в записях действий
Названия чисел в записях действий Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов Физические величины
Физические величины Преобразование подобия
Преобразование подобия Знакомство с клеткой
Знакомство с клеткой Числа 6 и 7. Письмо цифры 6
Числа 6 и 7. Письмо цифры 6