Содержание
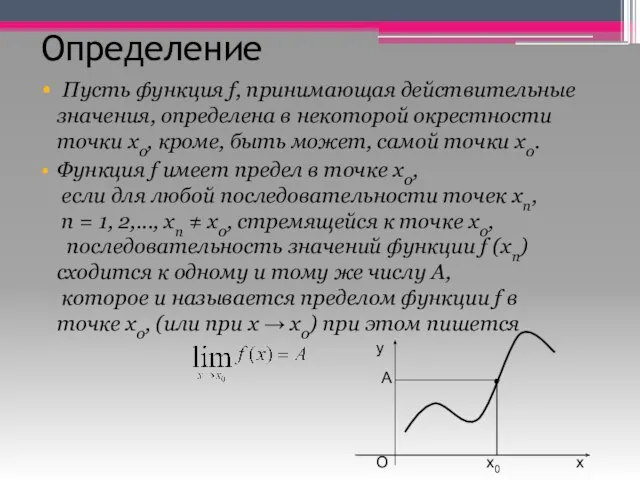
- 2. Определение Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может,
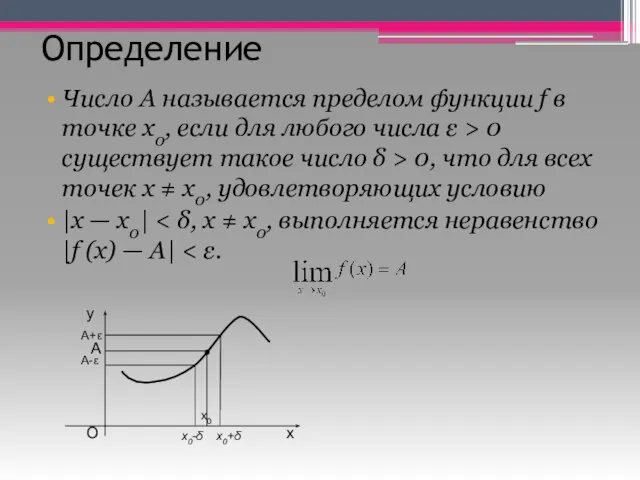
- 3. Определение Число А называется пределом функции f в точке x0, если для любого числа ε >
- 4. Все основные элементарные функции: постоянные, степенная функция (хα), показательная функция (ax), тригонометрические функции (sinx, cosx, tgx
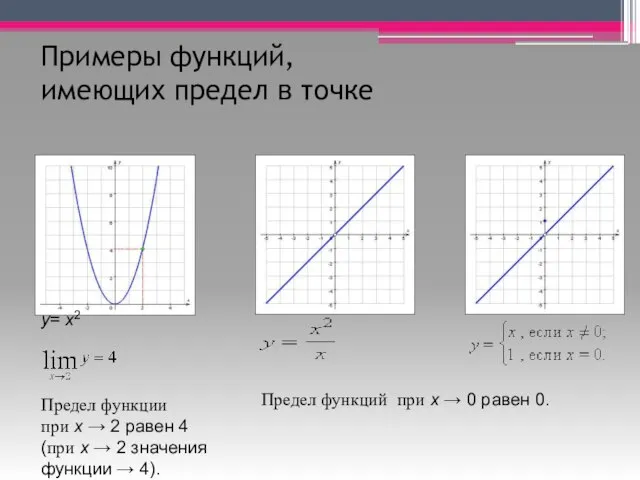
- 5. Примеры функций, имеющих предел в точке у= x2 Предел функции при x → 2 равен 4
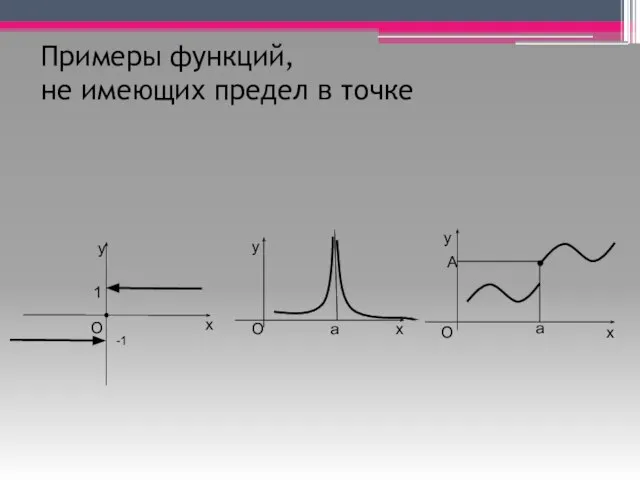
- 6. Примеры функций, не имеющих предел в точке
- 7. Свойства предела функции в точке Если функции f (x) и g (x) имеют конечные пределы в
- 8. Вычисление предела функции в точке Найдем Предел числителя Предел знаменателя . Используя теорему о пределе частного,
- 9. Найдем Предел числителя Предел знаменателя равен нулю, поэтому теорему о пределе частного применять нельзя. Величина 1/(x-3)
- 10. Раскрытие неопределенности При нахождении предела иногда сталкиваются с неопределенностями вида Отыскание предела в таких случаях называется
- 11. Разделим числитель и знаменатель на х4
- 12. Разделим числитель и знаменатель на х2 подразумевается не деление на ноль (делить на ноль нельзя), а
- 13. Вычислить предел Сначала попробуем подставить -1 в дробь: В данном случае получена так называемая неопределенность 0/0
- 14. Метод умножения числителя и знаменателя на сопряженное выражение Найти предел Сначала пробуем подставить 3 в выражение
- 16. Замечательные пределы первый замечательный предел второй замечательный предел
- 17. Примеры
- 18. Односторонние пределы Число A1 называется пределом функции f (x) слева в точке a, если для каждого
- 19. Предел функции справа Число A2 называется пределом функции f (x) справа в точке a, если для
- 21. Скачать презентацию













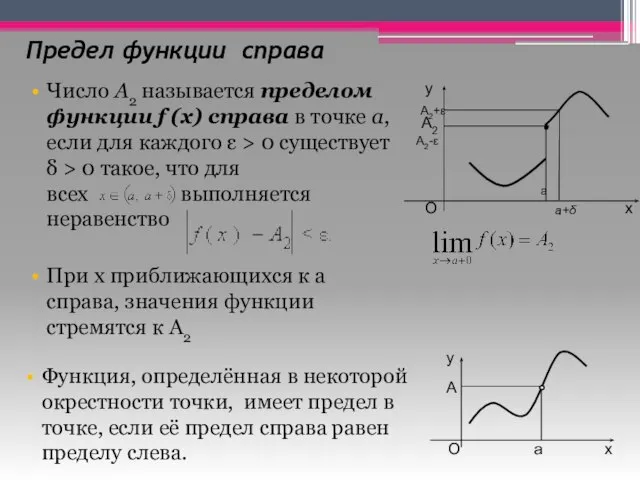
 Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Представляют геометрические фигуры
Представляют геометрические фигуры Матрицы. 1 часть
Матрицы. 1 часть Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Случаи сложения вида +5
Случаи сложения вида +5 Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Формула Пика
Формула Пика Перпендикулярность плоскостей
Перпендикулярность плоскостей Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов
Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах
П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Математический марафон. Интеллектуальная игра
Математический марафон. Интеллектуальная игра Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса
Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса Задания с фигурами
Задания с фигурами Алгебра в жизни человека
Алгебра в жизни человека Презентация на тему Арифметическая прогрессия: практикум
Презентация на тему Арифметическая прогрессия: практикум 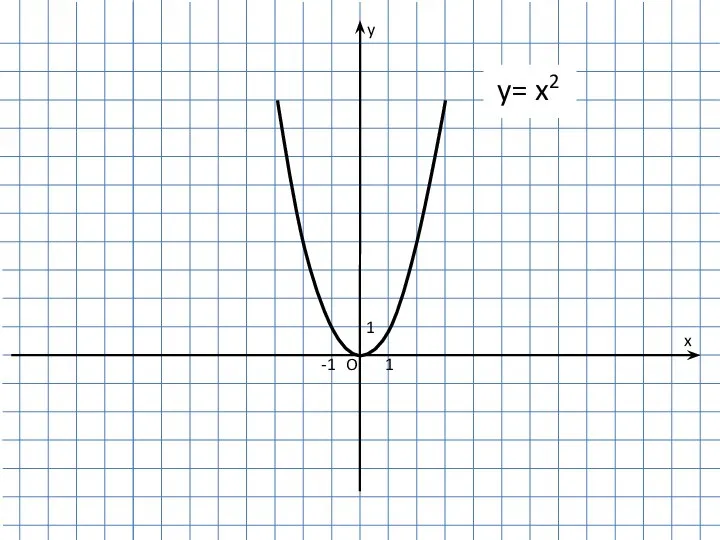 Функция y= x2
Функция y= x2 Семь чудес Кузбасса 5 класс
Семь чудес Кузбасса 5 класс Неравенство треугольника (7 класс)
Неравенство треугольника (7 класс) Формулы сокращенного умножения. Космический час на планете знаний
Формулы сокращенного умножения. Космический час на планете знаний Теория множеств
Теория множеств Многоугольники
Многоугольники Уравнение линии на плоскости
Уравнение линии на плоскости Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ  Прибавить и вычесть число 1
Прибавить и вычесть число 1 Площади и объемы многогранников. Решение задач
Площади и объемы многогранников. Решение задач