Содержание
- 34. На Руси самое древнее сочинение по арифметике, сохранившееся до нас, написано в 1196 году новгородским монахом
- 35. В других рукописях («Книга и письма» и другие) даются правила изменения площадей, нахождения расстояний, определение объемов
- 36. В течении 17 века геометрические знания на Руси распространялись медленно. В 18 веке геометрия получила большое
- 63. Пространственные отношения. Геометрические фигуры. • описывать взаимное расположение предметов в пространстве и на плоскости; • распознавать,
- 64. Геометрические величины. измерять длину отрезка; вычислять периметр треугольника, прямоугольника и квадрата, площадь прямоугольника и квадрата; оценивать
- 65. ОТКРЫТОГО ТИПА ЗАКРЫТОГО ТИПА шаблонность мышления пассивность неумение применять знания изменившейся ситуации уход от известных ответов
- 66. Примеры задач открытого типа
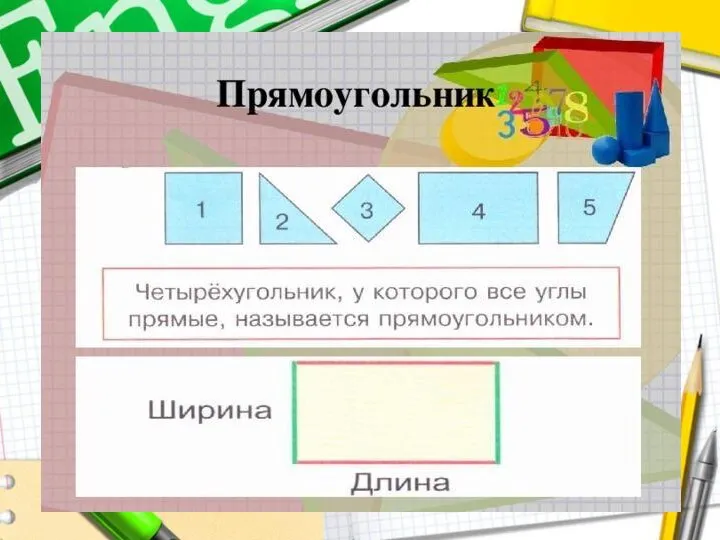
- 69. Задача. Прямоугольный лист бумаги разделили двумя отрезками на два листа треугольной формы и два четырёхугольной. Как
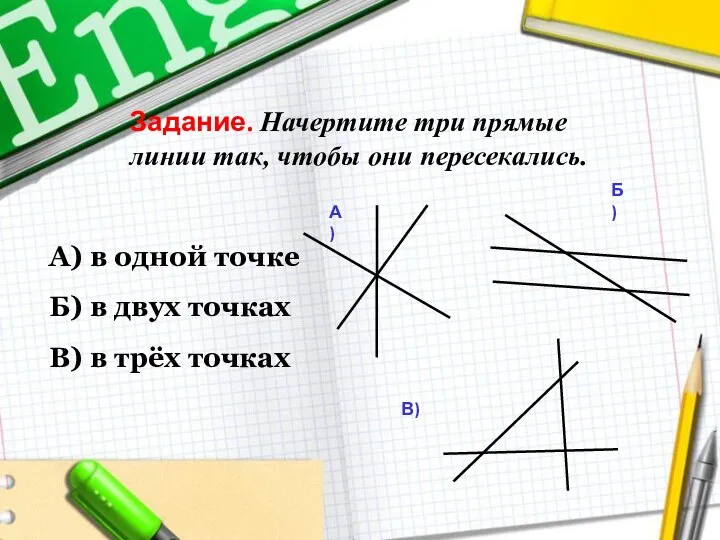
- 70. Задание. Начертите три прямые линии так, чтобы они пересекались. А) в одной точке Б) в двух
- 71. Задача. Возьмите три палочки. Составьте из них фигуру так, чтобы конец одной палочки совпадал с началом
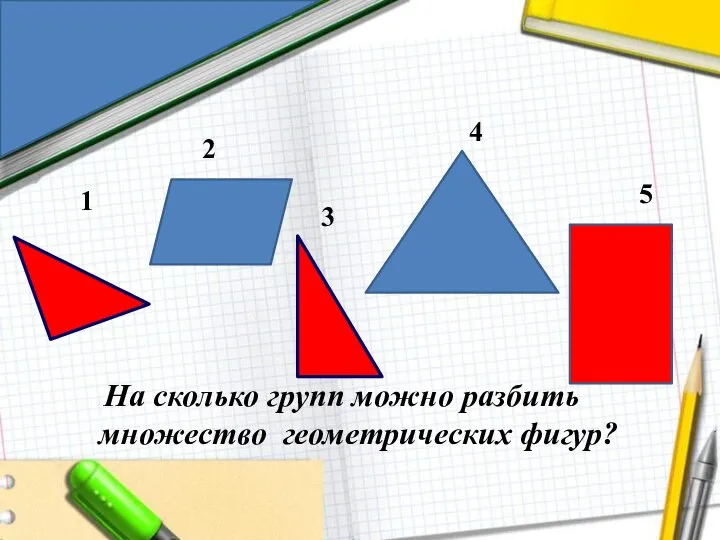
- 72. На сколько групп можно разбить множество геометрических фигур? 1 2 3 4 5
- 73. Рациональные способы решения задач 1+3+2+4=10 см II способ 2+2+2+2=8 см I способ 2х4=8 см Стороны четырёхугольника
- 76. Скачать презентацию
































































 Непериодические бесконечные десятичные дроби
Непериодические бесконечные десятичные дроби Конструктор (2)
Конструктор (2) Решение задач на увеличение числа в несколько раз
Решение задач на увеличение числа в несколько раз Сложение вида 37+48. Урок №71
Сложение вида 37+48. Урок №71 Степень числа
Степень числа Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Представьте данные смешанные числа в виде неправильных дробей
Представьте данные смешанные числа в виде неправильных дробей Треугольник Паскаля
Треугольник Паскаля Тригонометрические уравнения. Уравнение cos x=a
Тригонометрические уравнения. Уравнение cos x=a Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8
Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8 Состав чисел (тренажёр)
Состав чисел (тренажёр) Деловая игра Строитель. Тема: Площади многоугольников
Деловая игра Строитель. Тема: Площади многоугольников Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен История зарождения и развития геометрии
История зарождения и развития геометрии Решение текстовых задач на ЕГЭ
Решение текстовых задач на ЕГЭ Метод Гаусса
Метод Гаусса Умножение трёхзначного числа на однозначное
Умножение трёхзначного числа на однозначное Дифференциальные уравнения
Дифференциальные уравнения Компланарные вектора
Компланарные вектора Прямая. Плоскость
Прямая. Плоскость Свойства параллельных плоскостей (10 класс)
Свойства параллельных плоскостей (10 класс) Возведение в степень. Произведения и степени
Возведение в степень. Произведения и степени Презентация на тему Показательная функция: свойства, график
Презентация на тему Показательная функция: свойства, график  Ряды распределения
Ряды распределения Презентация на тему ЗАДАЧИ НА ПОСТРОЕНИЕ
Презентация на тему ЗАДАЧИ НА ПОСТРОЕНИЕ 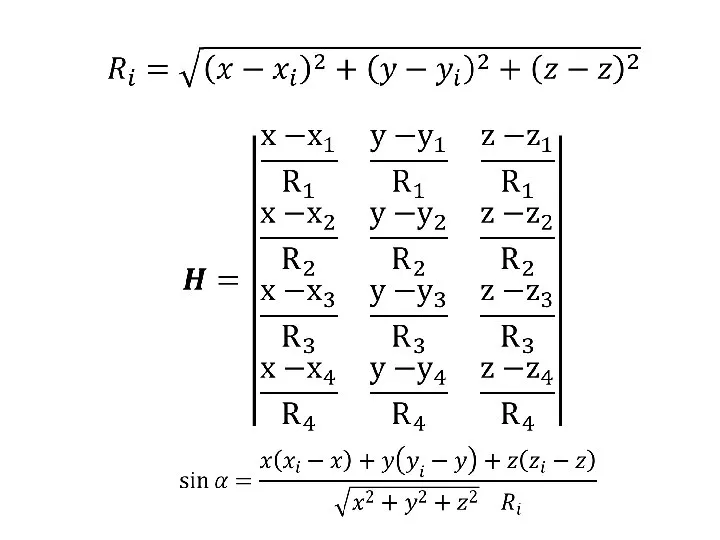 Геометрический фактор
Геометрический фактор Построение равнобедренного треугольника
Построение равнобедренного треугольника