Содержание
- 2. Цели урока. Повторить свойства логарифмов Решать задачи Решать уравнения Ввести понятия натурального и десятичного логарифмов
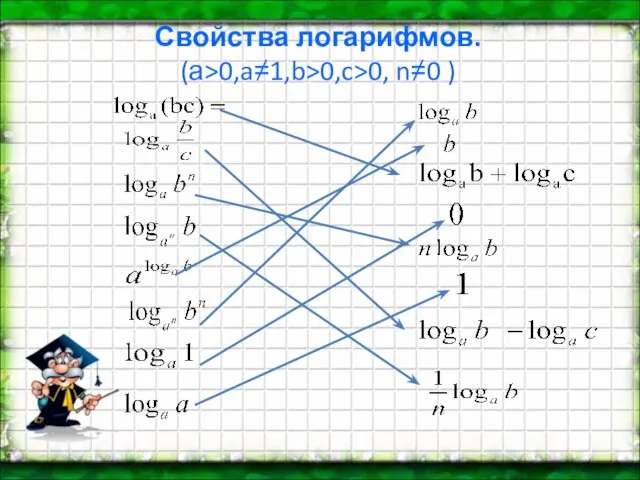
- 3. Свойства логарифмов. (а>0,a≠1,b>0,c>0, n≠0 ) :
- 4. Найдите значение выражений 4 - 0,5 -0,5 4 3 9 3 25 1 1 -2 2
- 5. Решите уравнение
- 6. Сравните ответы
- 7. Проблема Обратите внимание - действия с логарифмами возможны только при одинаковых основаниях! А если основания разные!?
- 8. Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg , т.е. log 10 m =
- 9. Переход к другому основанию Теорема Пусть дан логарифм loga b. Тогда для любого числа c такого,
- 10. Воспользуемся сначала свойством Теперь перейдем к основанию 2 loga b
- 11. 2) Найдите значение выражения loga b
- 12. 3)Найдите значение выражения , если Решение: Решение: Ответ: 12
- 13. Тренировочный тест 1.Вычислить: 0,3log0,32 – 5 – 4,91; 2) – 4,7; 3) – 3; 4) 2.
- 14. ДОМАШНЕЕ ЗАДАНИЕ Базовый(задание(я) для всех): Изучить§3, до задачи 3стр. 248-249, № 799(2,4), 800(2,4,6,8) Повышенный(задание(я) по выбору):
- 15. Первое упоминание натурального логарифма сделал Николас Меркатор в в 1668 году, хотя учитель математики Джон Спайделл
- 16. Происхождение термина натуральный логарифм Сначала может показаться, что поскольку наша система счисления имеет основание 10, то
- 17. е=2,718281828459045235360…. Саму константу впервые вычислил швейцарский математик Бернулли в ходе решения задачи о предельной величине процентного
- 18. Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его
- 20. Скачать презентацию
















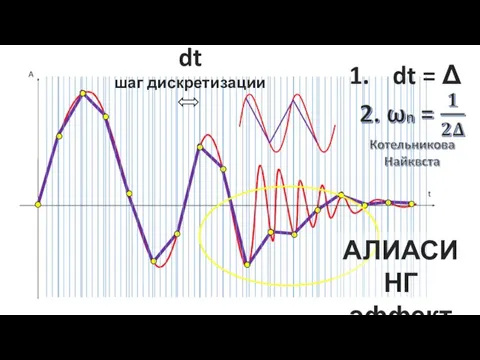 Алиасинг эффект. АЦП σ-δ. Интегратор
Алиасинг эффект. АЦП σ-δ. Интегратор Пропорция
Пропорция От землемерия к геометрии
От землемерия к геометрии Множества и операции над множествами
Множества и операции над множествами Квадратные уравнения
Квадратные уравнения Применение производной к исследованию функции и построению графика функции
Применение производной к исследованию функции и построению графика функции Проверка статистических гипотез
Проверка статистических гипотез В мире чисел и цифр
В мире чисел и цифр Числовые и буквенные выражения
Числовые и буквенные выражения Оптико–геометрические иллюзии
Оптико–геометрические иллюзии Свойства функции (10 класс)
Свойства функции (10 класс) Ряды распределения в статистике
Ряды распределения в статистике Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач
Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач Комбинаторные задачи
Комбинаторные задачи Монотонность функции
Монотонность функции Тригонометрические формулы суммы и разности углов
Тригонометрические формулы суммы и разности углов Степенная функция
Степенная функция Цифровые микроэлектронные устройства комбинационного типа
Цифровые микроэлектронные устройства комбинационного типа Арифметические, строковые и логические выражения. Учитель информатики МКОУ «СОШ с.Петропавловка» Бычкова О.В.
Арифметические, строковые и логические выражения. Учитель информатики МКОУ «СОШ с.Петропавловка» Бычкова О.В. Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Параллельные прямые
Параллельные прямые Математический КВН
Математический КВН Таблица умножения
Таблица умножения Решение задач. Штрих Шеффера
Решение задач. Штрих Шеффера Подобие. Коэффициент подобия
Подобие. Коэффициент подобия Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Симметрия. Виды симметрии
Симметрия. Виды симметрии Построение сечений тетраэдра
Построение сечений тетраэдра