Содержание
- 2. КОНТРОЛЬНЫЕ ВОПРОСЫ Какое уравнение называется дифференциальным? Что называется решением дифференциального уравнения? Какое решение дифференциального уравнения называется
- 3. Рассмотрим задачи, приводящие к дифференциальным уравнениям Задача №1 Найти закон движения точки, если её скорость задается
- 4. Задача №2 Составить уравнение кривой, проходящей через точку А(2;5), если угловой коэффициент касательной равен 2x Решение:
- 5. В предыдущих задачах решались уравнения, содержащие производные. Это и есть дифференциальные уравнения ОПРЕДЕЛЕНИЕ . Дифференциальным уравнением
- 6. Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала) входящего в данное уравнение Решением дифференциального уравнения
- 7. Различают общее и частное решения дифференциальных уравнений Общее решение – содержит произвольные постоянные (по числу порядка)
- 8. Условия, задающие значения функции в фиксированной точке называются начальными условиями (условиями Коши): Задача решения уравнения удовлетворяющего
- 9. Отличия алгебраического уравнения от дифференциального: 1)Алгебраическое уравнение– это зависимость между Дифференциальное –выражает соотношение между 2)Решением алгебраического
- 10. Дифференциальные уравнения первого порядка с разделенными переменными Общий вид первого порядка: 1)Если дифференциальное уравнение можно привести
- 11. Алгоритм решения дифференциальных уравнения с разделяющими переменными 1)Производную записать через дифференциальные уравнения 2)Члены уравнения с одинаковыми
- 12. Решить уравнение
- 13. Задача Найти закон движения тела по оси ох, если оно начало двигаться из точки М (4;
- 14. ДОМАШНЕЕ ЗАДАНИЕ Из предложенных дифференциальных уравнений выбрать любые три и найти их общее и частное решение
- 16. Скачать презентацию













 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Величины. Длина
Величины. Длина Случайные величины 14 сен
Случайные величины 14 сен Возникновение первых математических понятий
Возникновение первых математических понятий Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс
Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс Умножение на 1 и 0
Умножение на 1 и 0 Диктант по геометрии
Диктант по геометрии Выбор схемы измерения переменных
Выбор схемы измерения переменных Умножение на 10,100,1000, 0,1, 0,01, 0,001
Умножение на 10,100,1000, 0,1, 0,01, 0,001 Подготовка к блиц-турниру
Подготовка к блиц-турниру Скалярное прозведение векторов
Скалярное прозведение векторов Шифр Цезаря
Шифр Цезаря Сфера и шар
Сфера и шар Многогранники. Призма
Многогранники. Призма Пропорции и проценты
Пропорции и проценты Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число Графический диктант
Графический диктант Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника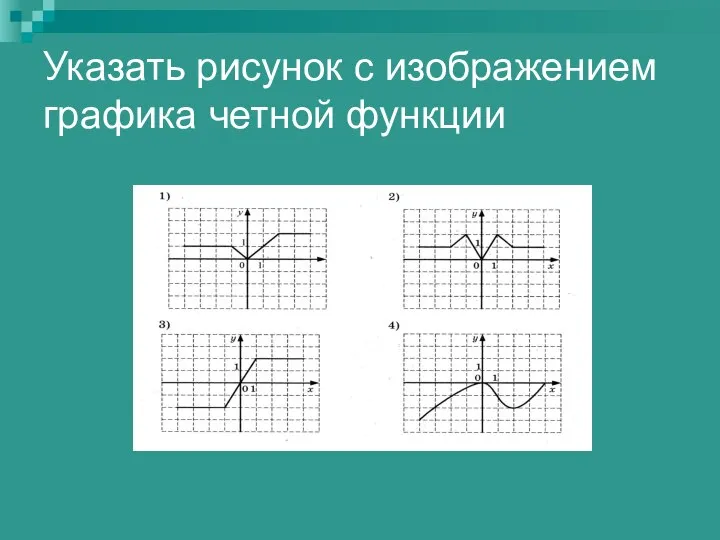 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Параллелепипед
Параллелепипед Выражение отношения в процентах
Выражение отношения в процентах Задачи на проценты. Схемы
Задачи на проценты. Схемы Решение нелинейных уравнений
Решение нелинейных уравнений Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика