Касательная к окружности

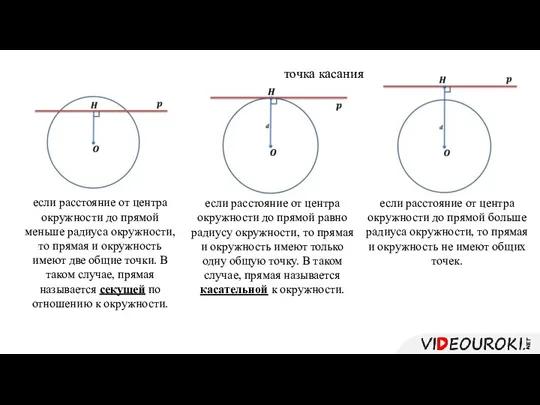
если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки. В таком случае, прямая называется секущей по отношению к окружности.
если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. В таком случае, прямая называется касательной к окружности.
если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
точка касания

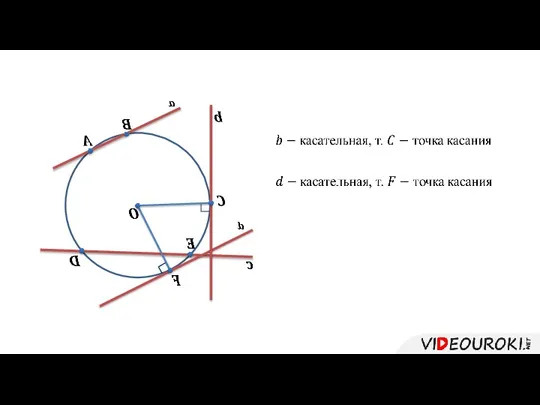
Теорема (свойство касательной). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Доказательство.

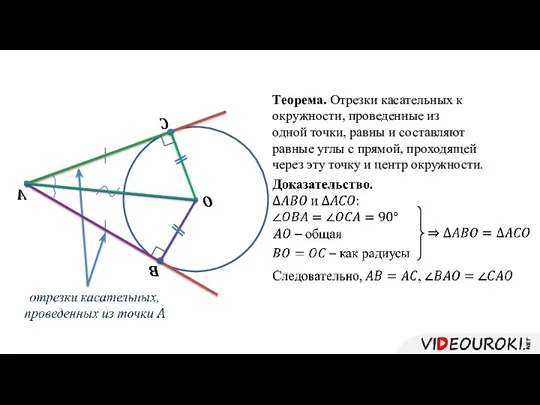
Теорема. Отрезки касательных к
окружности, проведенные из
одной точки, равны и составляют
равные углы с прямой, проходящей
через эту точку и центр окружности.

Решение.

Теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой.
А значит, он является расстоянием от центра окружности до прямой.
То есть радиус окружности и расстояние до прямой равны.
Доказательство.

Решение.

Решение.

Задача. Доказать, что касательные к окружности, проведенные через концы диаметра, параллельны.
Решение.

Решение.