Слайд 2Представление исходных данных
Yt1, Yt2, Yt3………………Ytn

Слайд 3Представление исходных данных
У1 Х11 Х12 …………X1k
У2 Х21 Х22 …………X2k
… ………… ………
Уn Xn1

Xn2 …………Xnk
n > k ~ 3
Слайд 4Представление исходных данных
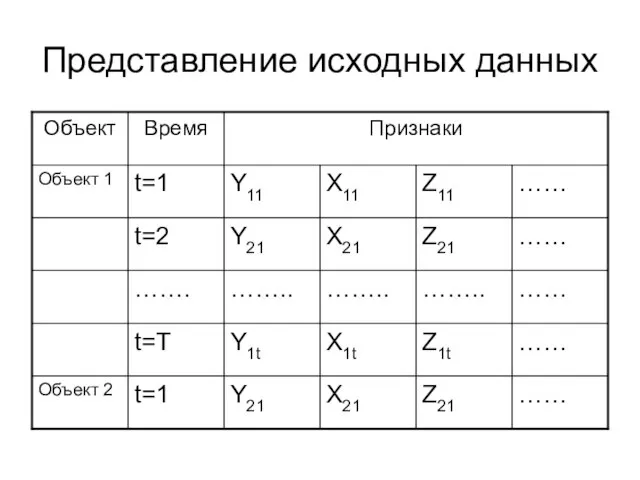
Слайд 5Построение корреляционно-регрессионной модели
У=в0+в1*х1+в2*х2 + … BkXk +ε

Слайд 6Оценка параметров модели
Оценка параметра называется несмещенной, если ее математическое ожидание равно оцениваемому

параметру
Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру при возрастании количества наблюдений
Оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди возможных несмещенных оценок параметра, вычисленных по выборкам одного и того же объема n
Слайд 7Требования к исходным данным
Объясняющие переменные х1, х2…..хк рассматриваются как неслучайные величины
Величины х1,

х2…..хк не связаны между собой линейной функциональной зависимостью
Слайд 8Требования к регрессионным остаткам
Регрессионные остатки εi есть взаимонезависимые случайные величины с нулевым

математическим ожиданием
Регрессионные остатки εi имеют постоянную остаточную дисперсию
Вектор регресионных остатков подчиняется n-мерному нормальному закону распределения вероятностей
Слайд 9Исходная информация
В=(ХтХ)-1ХтУ
У1 1 Х11 Х12
У2 1 Х21 Х22
… …………
Уn 1

Xn1 Xn2
Слайд 10Используемые функции
Хт транспонированная матрица.
Копировать, специальная вставка, выбрать окошко «транспонировать», ввод
МУМНОЖ
МОБР
Shift + Alt

+ Enter
Слайд 11Оценка значимости уравнения в целом
Fрасч =

Слайд 12Сравнение расчетного и табличного значения
Fтабл =FРАСПОБР
Вероятность = вероятности ошибки
V1 = K+1
V2 =

n-k-1
Fрасч > Fтабл Уравнение значимо
Слайд 13Оценка значимости регрессоров
Tbj = bj/sbj
Ковариационная матрица по bj
S*(XтХ)-1
S2 = Qост/(n-k-1)
По диагонали

этой матрицы находим Sbj в квадрате
Слайд 14Определение значимости регрессоров
tтабл = СТЬЮДРАСПОБР
Вероятность ошибки
V1=n-k-1
tрасч > tтабл по абсолютной величине, то

регрессор значим
Слайд 15Множественный коэффициент детерминации
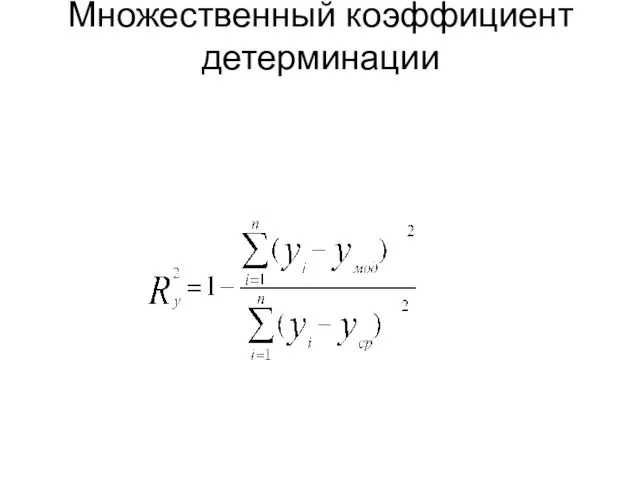
Слайд 16Точечный и интервальный прогноз
Расчет прогнозных значений по лекциям
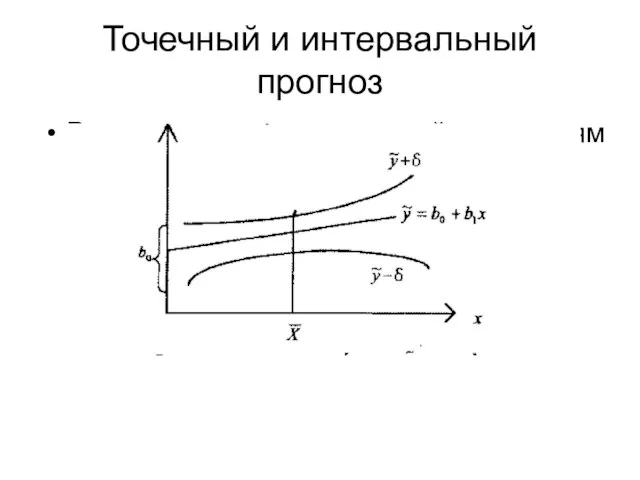
Слайд 17Расчет интервального прогноза для простейшей модели
Yn+1∈Yn+1 ±tтS














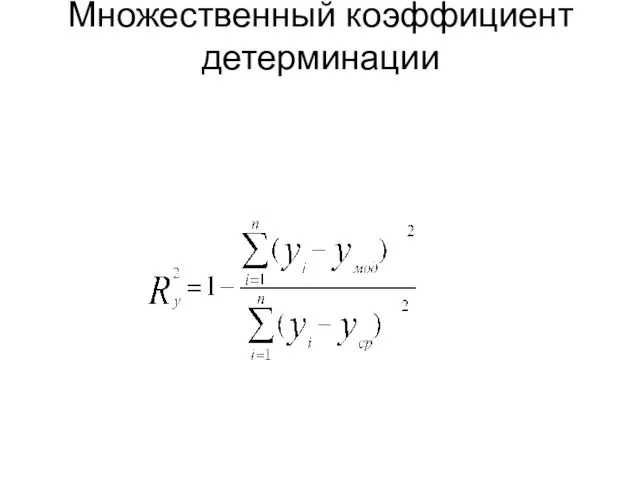


 Проекция вершин, ребер и граней
Проекция вершин, ребер и граней Решение квадратных уравнений. 8 класс
Решение квадратных уравнений. 8 класс Факториал
Факториал Обратные матрицы
Обратные матрицы Матрицы. Прямоугольная таблица
Матрицы. Прямоугольная таблица Симметрия в искусстве
Симметрия в искусстве Решение задач. Пирамида
Решение задач. Пирамида Дифференциальные уравнения
Дифференциальные уравнения Измерение углов (5 класс)
Измерение углов (5 класс) Осевое сечение конуса и цилиндра
Осевое сечение конуса и цилиндра Математическая логика и теория алгоритмов
Математическая логика и теория алгоритмов ЕГЭ по профильной математике. Прототипы №3
ЕГЭ по профильной математике. Прототипы №3 Неопределенный интеграл. Методы интегрирования
Неопределенный интеграл. Методы интегрирования Дискриминантный анализ
Дискриминантный анализ Названия чисел в записях действий
Названия чисел в записях действий Степень.Симон Стевин
Степень.Симон Стевин Свойства параллелограмма
Свойства параллелограмма Координатная плоскость 6 класс - Презентация по математике_
Координатная плоскость 6 класс - Презентация по математике_ Квадратичная функция. Подготовка к ГИА
Квадратичная функция. Подготовка к ГИА Решение задач на нахождение площади фигур. 6 класс
Решение задач на нахождение площади фигур. 6 класс Презентация на тему Функция у=х^2, её свойства и график
Презентация на тему Функция у=х^2, её свойства и график  Тренировочный вариант №98
Тренировочный вариант №98 Математика
Математика Работа по математике. Симметрия
Работа по математике. Симметрия Одночлены
Одночлены Цена деления и предел измерения линейки
Цена деления и предел измерения линейки Вычисление по статистики
Вычисление по статистики Функция y = x2 и её график
Функция y = x2 и её график