Слайд 2Ричард Беллман
Ричард Эрнст Беллман (англ. Richard Ernest Bellman; 1920—1984) — американский математик, один из ведущих специалистов

в области математики и вычислительной техники.
Слайд 3Последовательность Фибоначчи
Последовательность Фибоначчи Fn задается формулами: F1 = 1, F2 = 1,
Fn = Fn – 1 + Fn – 2 при n > 1.
Необходимо найти Fn по номеру n.

Слайд 4Рекурсия
int F(int n) {
if (n < 2) return 1;

else return F(n - 1) + F(n - 2);
}
Слайд 5Сохранение промежуточных результатов
int F(int n) {
if (A[n] != -1) return
![Сохранение промежуточных результатов int F(int n) { if (A[n] != -1) return](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-4.jpg)
A[n];
if (n < 2) return 1;
else {
A[n] = F(n - 1) + F(n - 2);
return A[n];
}
}
Слайд 6Самое простое решение
F[0] = 1;
F[1] = 1;
for (i = 2;
![Самое простое решение F[0] = 1; F[1] = 1; for (i =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-5.jpg)
i < n; i++) {
F[i] = F[i - 1] + F[i - 2];
}
Слайд 7Одномерное динамическое программирование
Задача 1. Посчитать число последовательностей нулей и единиц длины n, в которых
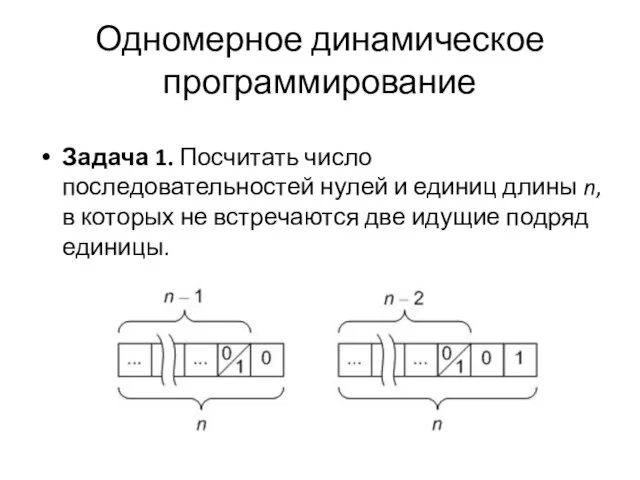
не встречаются две идущие подряд единицы.
Слайд 8Двумерное динамическое программирование
Задача 2. Дано прямоугольное поле размером n*m клеток. Можно совершать шаги
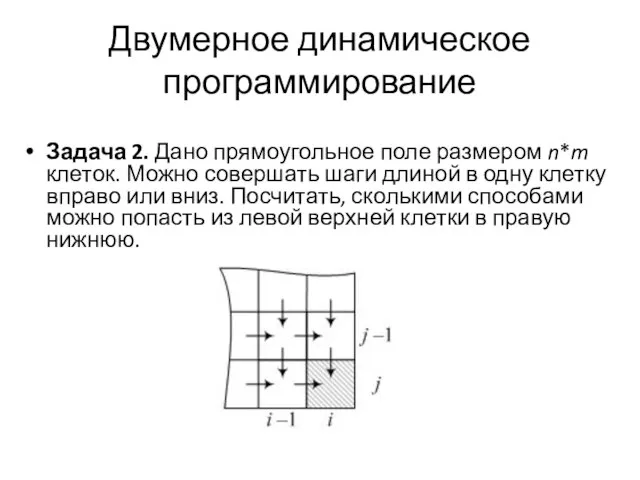
длиной в одну клетку вправо или вниз. Посчитать, сколькими способами можно попасть из левой верхней клетки в правую нижнюю.
Слайд 9Задача о рюкзаке
Имеется набор из N предметов, каждый предмет имеет массу Wi

и стоимость Pi, i=(1,2..N), требуется собрать набор с максимальной полезностью таким образом, чтобы он имел вес не больше W, где W – вместимость ранца. Wi , Pi , W – целые неотрицательные числа.
Слайд 10Методы
Полный перебор
Динамическое программирование
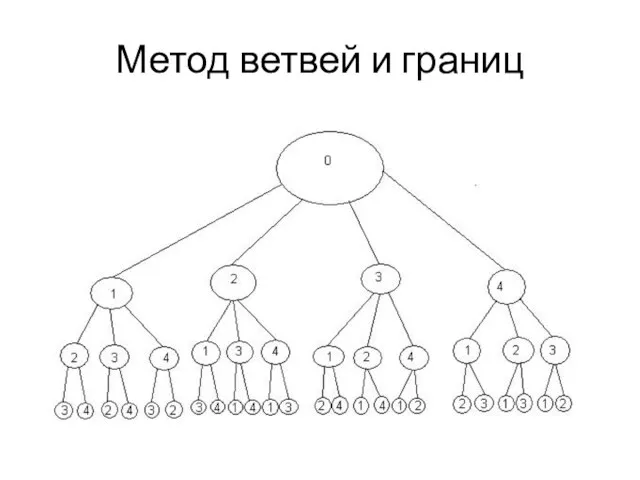
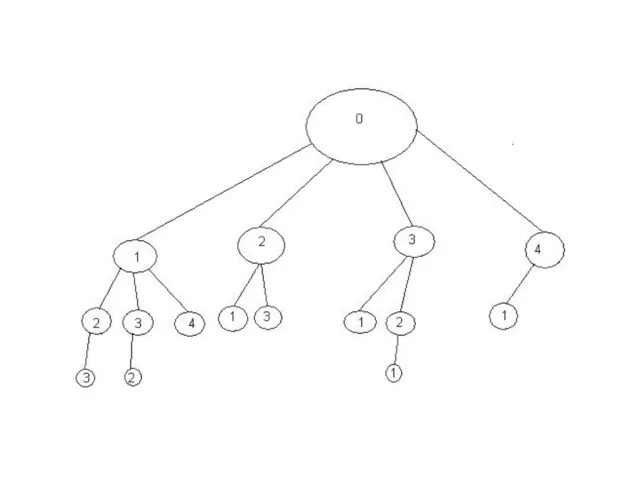
Метод ветвей и границ
Жадный алгоритм

Слайд 11Динамическое программирование
Value [W, N] – максимальная сумма, которую надо найти.
Суть метода–
![Динамическое программирование Value [W, N] – максимальная сумма, которую надо найти. Суть](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-10.jpg)
на каждом шаге по весу 1
Слайд 12Если его взять то вес станет W-Wi , тогда Value[W, i] =
![Если его взять то вес станет W-Wi , тогда Value[W, i] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-11.jpg)
Value[W – Wi , i-1] + Pi (для Value[W – Wi , i-1] решение уже найдено остается только прибавить Pi).
Если его не брать то вес останется тем же и Value[W , i] = Value[W , i-1].
Из двух вариантов выбирается тот, который дает наибольший результат.



![Сохранение промежуточных результатов int F(int n) { if (A[n] != -1) return](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-4.jpg)
![Самое простое решение F[0] = 1; F[1] = 1; for (i =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-5.jpg)




![Динамическое программирование Value [W, N] – максимальная сумма, которую надо найти. Суть](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-10.jpg)
![Если его взять то вес станет W-Wi , тогда Value[W, i] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840434/slide-11.jpg)
 Решение логических задач с помощью таблиц и метода рассуждений
Решение логических задач с помощью таблиц и метода рассуждений Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график
Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график Моделирование. Объекты и их модели. (Тема 10)
Моделирование. Объекты и их модели. (Тема 10) Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе
Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе Rinjka liinija
Rinjka liinija Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе Возведение в куб суммы и разности
Возведение в куб суммы и разности Презентация на тему Статистика и математика
Презентация на тему Статистика и математика  Неравенства. Логарифмические неравенства
Неравенства. Логарифмические неравенства Случайные сигналы и их математические модели
Случайные сигналы и их математические модели Волшебная страна - Геометрия
Волшебная страна - Геометрия Презентация на тему Первообразная 11 класс
Презентация на тему Первообразная 11 класс  Прямоугольный параллелепипед
Прямоугольный параллелепипед Медiана, бiсектриса i висoта трикутника. (7 класс)
Медiана, бiсектриса i висoта трикутника. (7 класс) Карточки-задания по теме Конус. Содержат алгоритм решения
Карточки-задания по теме Конус. Содержат алгоритм решения Теорема, обратная теореме Виета
Теорема, обратная теореме Виета Решение уравнений. Бахчисарайский фонтан
Решение уравнений. Бахчисарайский фонтан Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Деление одночлена на одночлен
Деление одночлена на одночлен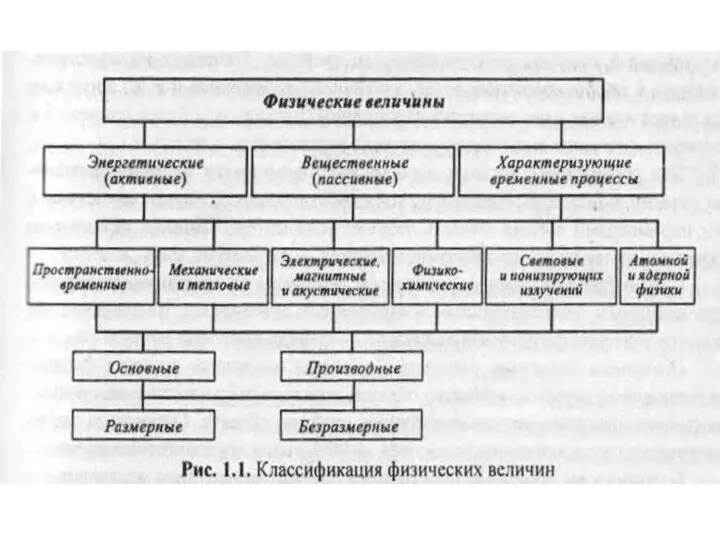 Физические величины
Физические величины Определители матриц
Определители матриц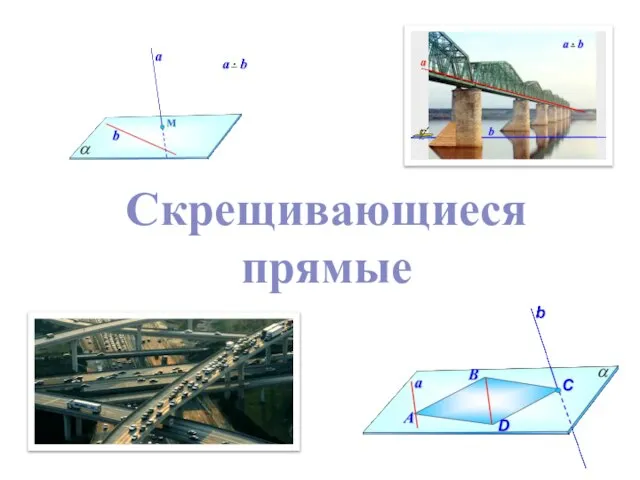 Скрещивающиеся прямые
Скрещивающиеся прямые Алгоритм решения уравнений
Алгоритм решения уравнений Школа волшебников
Школа волшебников Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций Задания для ЗНО
Задания для ЗНО Число и цифра 9
Число и цифра 9 Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин