Слайд 2 Задачи урока:
Повторить теоретический материал по теме «Квадратные уравнения»
Расширить знания об истории

возникновения квадратных уравнений.
Проверить умения определять виды квадратных уравнений
Совершенствовать умения в решении полных и неполных квадратных
уравнений
5. Закрепить умения в решении биквадратных уравнений и уравнений,
сводящихся к квадратным;
Слайд 3В класс вошел – не хмурь лица,
Будь разумным до конца.
Ты не зритель

и не гость –
Ты программы нашей гвоздь.
Не ломайся, не смущайся,
Всем законам подчиняйся.
Слайд 5История возникновения квадратных уравнений:
Необходимость решать уравнения
не только первой, но и второй

степени ещё в древности была
вызвана потребностью решать
задачи, связанные с нахождением
площадей земельных участков и с
земляными работами военного
характера, а также с развитием
астрономии и самой математики.
Квадратные уравнения умели
решать около 2000 лет до
нашей эры вавилоняне.
В их клинописных текстах встречаются, кроме неполных, также и полные квадратные уравнения.
Слайд 6Впервые квадратное уравнение сумели решить математики Древнего
Египта. Некоторые виды квадратных уравнений, сводя

их решение к
геометрическим построениям, могли решать древнегреческие математики , в ом числе и Эвклид.
Приемы решения уравнений без обращения к геометрии дает
Диофант Александрийский (III в).
Правило решения квадратных уравнений дал индийский ученый
Брахмагупта (VII в.).
Формулы решения квадратных уравнений в Европе были впервые
изложены в 1202 г. итальянским математиком Леонардом Фибоначчи.
Общее правило решения квадратных уравнений, приведенных к единому
виду ax2 + b + c = 0, было сформулировано в Европе лишь в 1544 г.
Штифелем. Вывод формулы решения квадратного уравнения в
общем виде имеется у Франсуа Виета, однако Виет признавал
только положительные корни. Лишь в XVII в. Благодаря трудам Декарта,
Ньютона и других ученых способ решения квадратных уравнений
принимает современный вид.
Слайд 8Чтобы решить уравнение,
Корни его отыскать.
Нужно немного терпения,
Ручку, перо и тетрадь.







 Теорема Пифагора
Теорема Пифагора У мольберта - математик
У мольберта - математик Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
Преобразование выражения Asinx+Bcosx к виду Csin(x+t) Операции над множествами
Операции над множествами Параллелепипед и куб. 3 класс
Параллелепипед и куб. 3 класс Устный счет. Пропорция
Устный счет. Пропорция Проект по математике. Цифра 5. 1 класс
Проект по математике. Цифра 5. 1 класс Использование прикладных программ для оптимизации задач исследования. Контрольная работа
Использование прикладных программ для оптимизации задач исследования. Контрольная работа Решение треугольников
Решение треугольников Презентация на тему Тренажёр «Квадратные корни»
Презентация на тему Тренажёр «Квадратные корни»  Линии на плоскости
Линии на плоскости Решение систем линейных неравенств
Решение систем линейных неравенств Сечения куба плоскостью
Сечения куба плоскостью Решение иррациональных уравнений
Решение иррациональных уравнений Тригонометрические уравнения
Тригонометрические уравнения Основные понятия комбинаторики
Основные понятия комбинаторики Таблицы. Геометрия
Таблицы. Геометрия Задачи на готовых чертежах. Подобные треугольники
Задачи на готовых чертежах. Подобные треугольники Логические задачи. 1 класс
Логические задачи. 1 класс Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби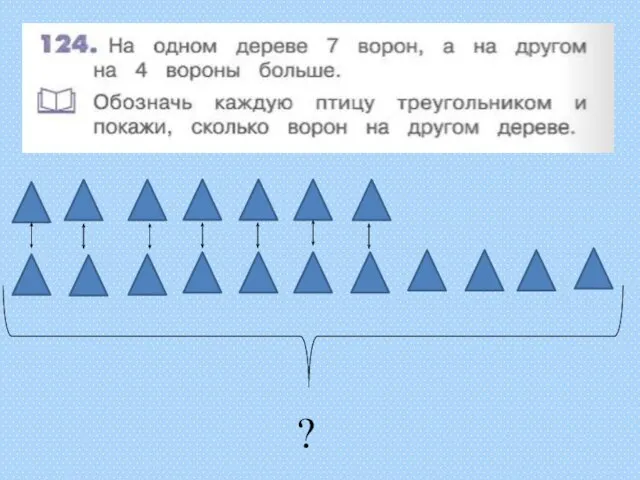 Треугольники, задача
Треугольники, задача ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ Сложение и вычитание вида +1 -1
Сложение и вычитание вида +1 -1 Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Режим поступления заявок
Режим поступления заявок Математика. 1 класс
Математика. 1 класс Правила нахождения производной
Правила нахождения производной Метод Галеркина для дифференциально-операторного уравнения третьего порядка
Метод Галеркина для дифференциально-операторного уравнения третьего порядка