Содержание
- 2. Будем обозначать случайные величины Х, а их возможные значения х. Например, пусть Х - число очков,
- 3. Случайная величина называется дискретной, если множество ее возможных значений cчетно (т.е. все возможные значения можно пронумеровать
- 4. Дискретная случайная величина полностью определяется своим рядом распределения. Ряд распределения представляет собой таблицу, в которой указаны
- 5. Поскольку ряд распределения содержит все возможные значения случайной величины, то суммарная вероятность должна быть равна 1.
- 6. ПРИМЕР. Рассмотрим опыт с бросанием двух игральных кубиков. Пусть случайная величина Х - сумма выпавших очков.
- 7. Р(X =1/36+2/36+3/36=6/36=1/6 Р(X>10)=P(X=11)+P(X=12)= =2/36+1/36=3/36=1/12 P(3 =3/36+4/36+5/36=12/36=1/3 Построим ряд распределения:
- 9. Скачать презентацию






 Частное и его значение
Частное и его значение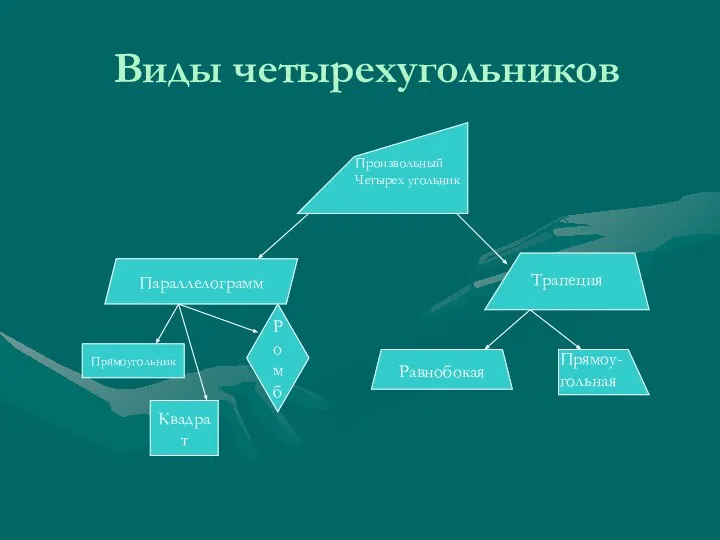 Виды четырехугольников
Виды четырехугольников Процентное содержание компонентов
Процентное содержание компонентов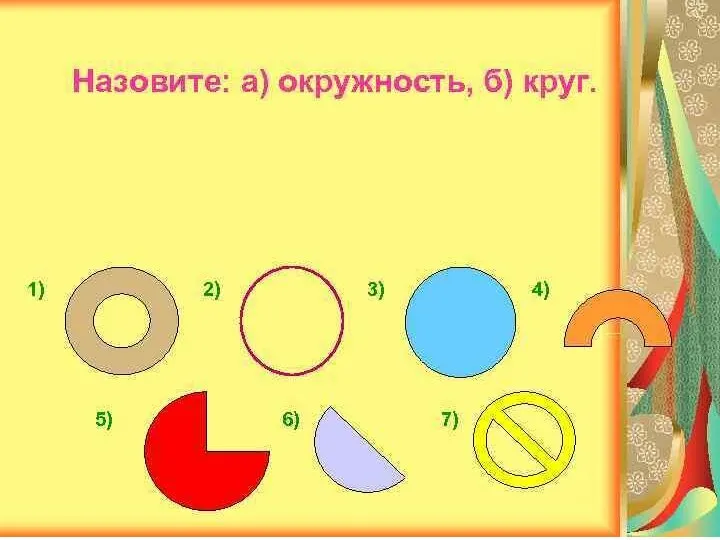 Окружность
Окружность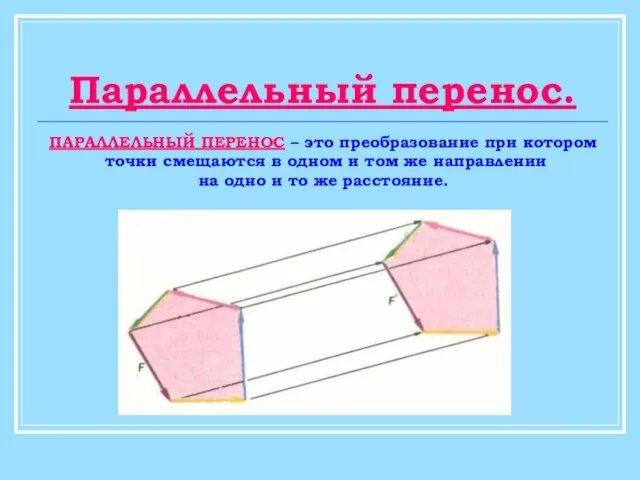 Параллельный перенос фигур
Параллельный перенос фигур Сущность экономического прогнозирования
Сущность экономического прогнозирования первые уроки геометрии
первые уроки геометрии Показательные неравенства
Показательные неравенства Стандартный вид числа
Стандартный вид числа Таблица сложения
Таблица сложения Окружность, круг, их элементы и части. Центральный угол. 7 класс
Окружность, круг, их элементы и части. Центральный угол. 7 класс Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Какую прямую называют координатной?
Какую прямую называют координатной? Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Презентация на тему Теорема синусов
Презентация на тему Теорема синусов  Теорема о неполноте
Теорема о неполноте Презентация на тему Технологии развивающего обучения в практике учителя математики
Презентация на тему Технологии развивающего обучения в практике учителя математики  Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Проект Математическая вертикаль. Геометрия. 8 класс
Проект Математическая вертикаль. Геометрия. 8 класс Задача з піцою
Задача з піцою Презентация на тему Место числового множителя в выражении с переменной
Презентация на тему Место числового множителя в выражении с переменной  Разложение функций в степенные ряды
Разложение функций в степенные ряды Иррациональные уравнения
Иррациональные уравнения Умножение
Умножение Геометрия в искусстве
Геометрия в искусстве Что такое дискретная математика?
Что такое дискретная математика? Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график סדר פעולות החשבון
סדר פעולות החשבון