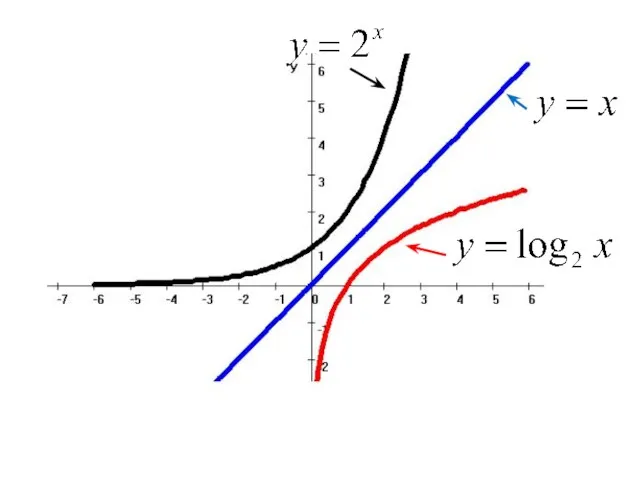
Слайд 2Определение.
Функция вида
называется показательной.

Слайд 4D(f) = R
Не является ни четной, ни нечетной (общего вида)
Возрастает на R
Не

ограничена сверху, ограничена снизу: f(x) > 0
Наибольшего значения не имеет, наименьшего значения не имеет
Непрерывна
Слайд 5Е(f) = (0; +∞)
Выпукла вниз на R
Дифференцируема в любой точке
Горизонтальная асимптота у
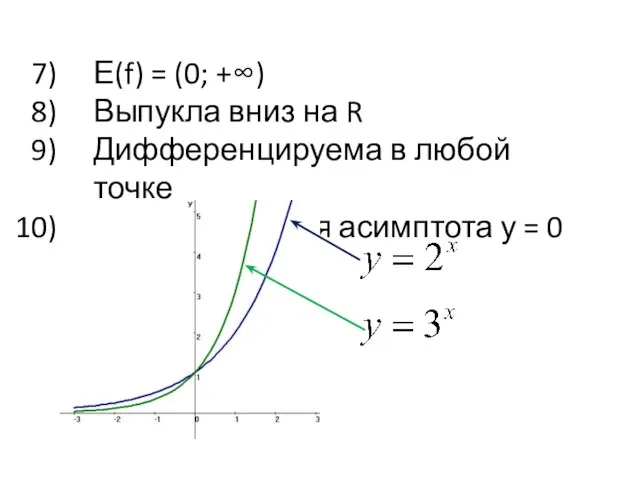
= 0
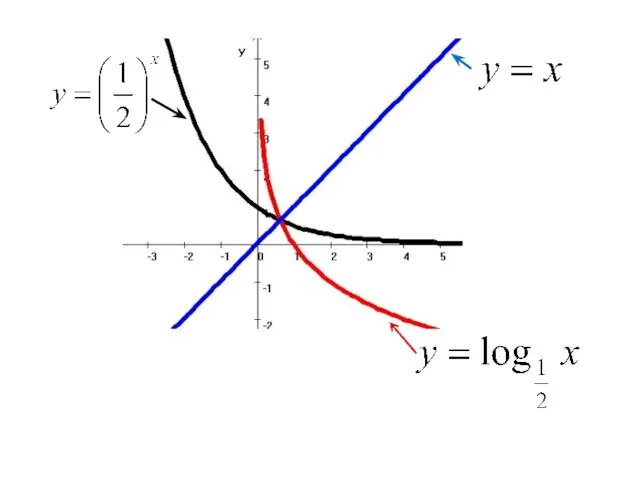
Слайд 7D(f) = R
Не является ни четной, ни нечетной (общего вида)
Убывает на R
Не

ограничена сверху, ограничена снизу: f(x) > 0
Наибольшего значения не имеет, наименьшего значения не имеет
Непрерывна
Слайд 8Е(f) = (0; ;+∞)
Выпукла вниз на R
Дифференцируема в любой точке
Горизонтальная асимптота y
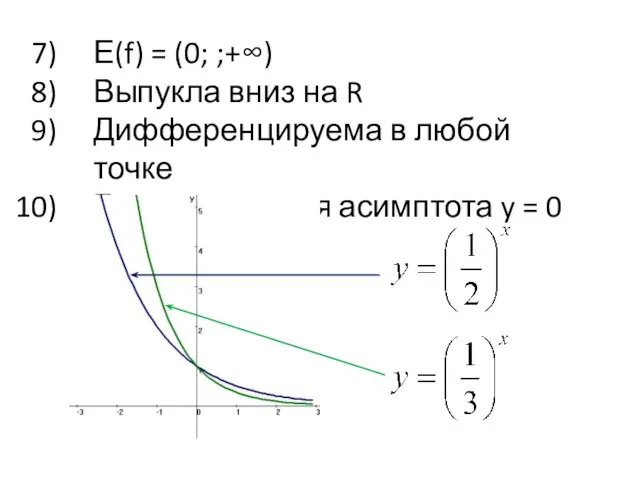
= 0
Слайд 9Определение.
Функцию, обратную к показательной
функции называют
логарифмической и обозначают

Слайд 11D(f) = (0; +∞)
Не является ни четной, ни нечетной (общего вида)
Возрастает на

(0; +∞)
Не ограничена ни сверху, ни снизу
Наибольшего значения не имеет, наименьшего значения не имеет
Непрерывна
Слайд 12Е(f) = (-∞; +∞)
Выпукла вверх на R
Дифференцируема в любой точке
Вертикальная асимптота х

= 0
Слайд 14D(f) = (0; +∞)
Не является ни четной, ни нечетной (общего вида)
Убывает на

(0;+∞)
Не ограничена ни сверху, ни снизу
Наибольшего значения не имеет, наименьшего значения не имеет
Непрерывна
Слайд 15Е(f) = (-∞; +∞)
Выпукла вниз на R
Дифференцируема в любой точке
Вертикальная асимптота х

= 0
Слайд 16Дифференцирование показательной функции
Интегрирование показательной функции












 Презентация на тему ОБЪЁМ ТЕЛ
Презентация на тему ОБЪЁМ ТЕЛ  Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Решение уравнений: рациональных и иррациональных
Решение уравнений: рациональных и иррациональных Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Это страшное слово: Параметр
Это страшное слово: Параметр Математика и живопись
Математика и живопись Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ  Тела вращения
Тела вращения Математический кроссворд
Математический кроссворд Графический метод решения уравнений. Задания для устного счета
Графический метод решения уравнений. Задания для устного счета Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Проецирование
Проецирование Тригонометрические функции двойного угла
Тригонометрические функции двойного угла Распределительное свойство умножения
Распределительное свойство умножения Геометрические фигуры
Геометрические фигуры Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Математика, Устный счёт
Математика, Устный счёт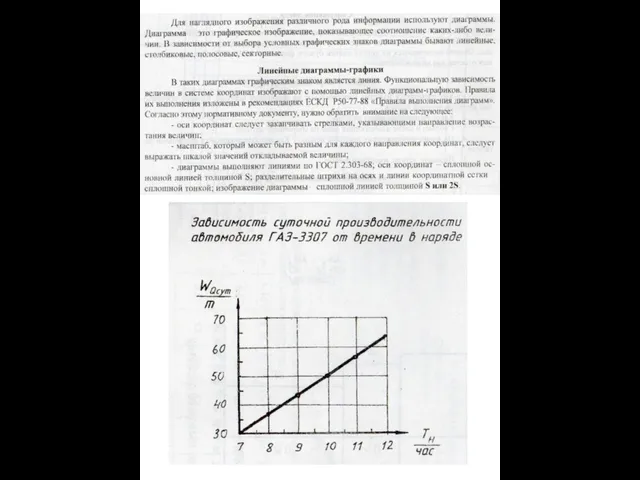 Графики и диаграммы
Графики и диаграммы Единицы измерения, масштабы шкал
Единицы измерения, масштабы шкал Некоторые методические приемы для работы с детьми ЗПР на уроках математики
Некоторые методические приемы для работы с детьми ЗПР на уроках математики Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности
Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Концентрация. Часть II
Концентрация. Часть II Отрицательные числа в географии
Отрицательные числа в географии