Содержание
- 2. Пример. Даны логические функции: Требуется доказать их равносильность по таблице истинности.
- 3. 2. С помощью эквивалентных преобразований Равносильности алгебры логики относительно базовых логических операций: Ассоциативность: x1 ▪ (x2
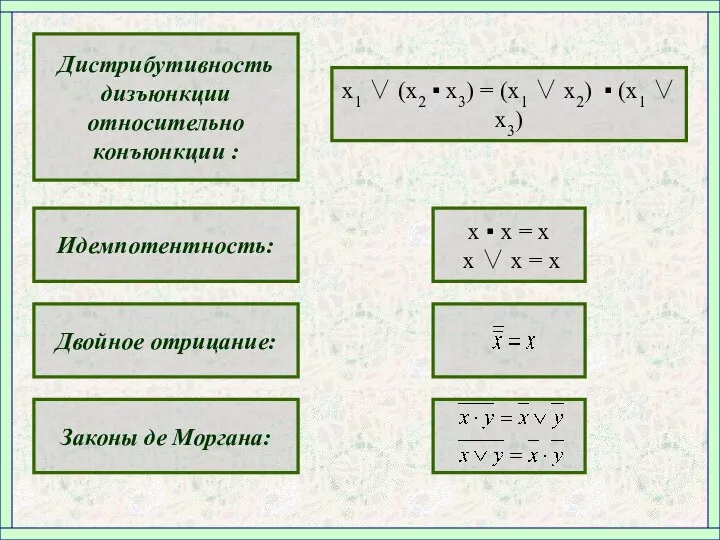
- 4. Дистрибутивность дизъюнкции относительно конъюнкции : x1 ∨ (х2 ▪ x3) = (x1 ∨ х2) ▪ (x1
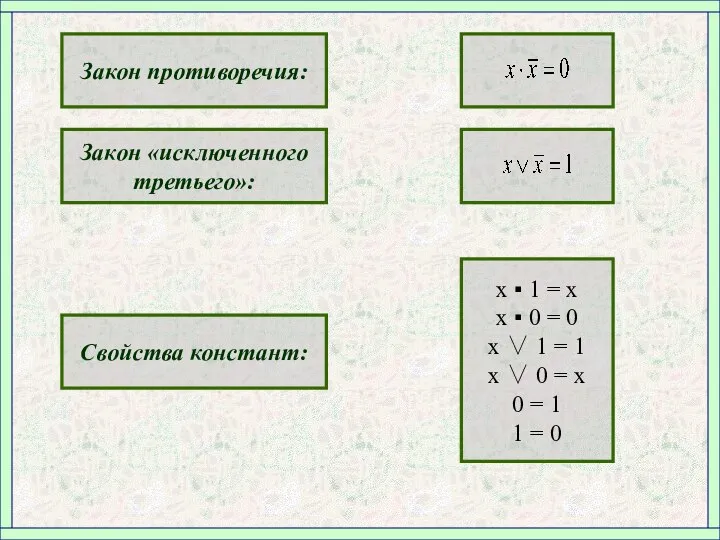
- 5. Закон противоречия: Закон «исключенного третьего»: Свойства констант: х ▪ 1 = х х ▪ 0 =
- 6. Все равносильности легко доказываются по таблицам истинности. Примеры. 1 х1 ∨ x1 ▪ x2 = x1
- 7. 3 x ▪ y ▪ x = x ▪ y x ▪ y ▪ x =
- 8. 6 (x1 ∨ х2) ▪ (x1 ∨ x3) = x1 ∨ х2 ▪ x3 (x1 ∨
- 10. Скачать презентацию





 Дроби и проценты. Арифметические действия с дробями
Дроби и проценты. Арифметические действия с дробями Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Число или цифра 2
Число или цифра 2 ОГЭ. Приемы решения практикоориентированных задач
ОГЭ. Приемы решения практикоориентированных задач Сложение и вычитание векторов
Сложение и вычитание векторов Сказочная математика
Сказочная математика Перестановочные тесты и бутстреп анализ
Перестановочные тесты и бутстреп анализ Теорема Виета и её применение
Теорема Виета и её применение Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций
Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций Презентация на тему ЗАДАЧИ НА ДРОБИ
Презентация на тему ЗАДАЧИ НА ДРОБИ  Практическое применение теоремы косинусов и синусов. 9 класс
Практическое применение теоремы косинусов и синусов. 9 класс Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Разряды и счет
Разряды и счет Графический метод
Графический метод Игра
Игра Отношение чисел
Отношение чисел Параллелограмм
Параллелограмм Задачи на перебор вариантов. 4 класс
Задачи на перебор вариантов. 4 класс Знакомство с образованием чисел второго десятка
Знакомство с образованием чисел второго десятка Системы уравнений. Задание №9. ОГЭ
Системы уравнений. Задание №9. ОГЭ График равномерного движения
График равномерного движения Площадь правильного треугольника
Площадь правильного треугольника Решение составных задач
Решение составных задач Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения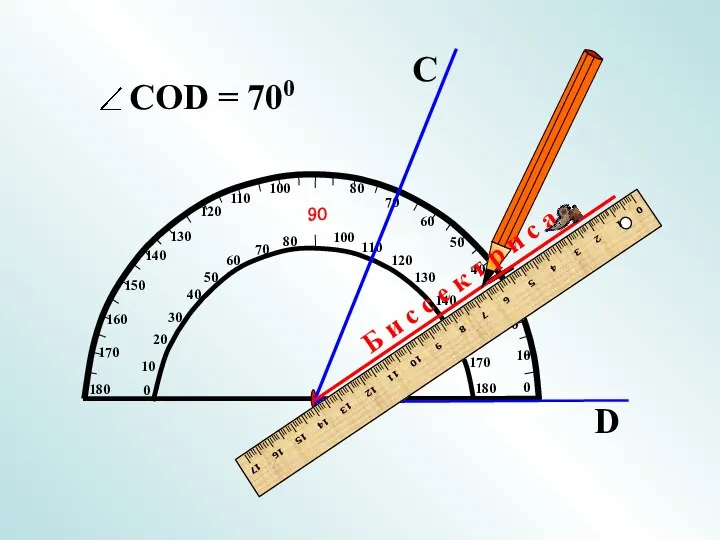 Биссектриса угла
Биссектриса угла Длина окружности. Площадь круга
Длина окружности. Площадь круга Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс