Содержание
- 2. Определения. 1.Секущая плоскость тетраэдра(параллепипеда)-это любая плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллепипеда).
- 3. Секущей плоскостью тетраэдра (параллелепипеда) называется любая плоскость, по обе стороны от которой имеются точки данного многогранника.
- 4. Две плоскости пересекаются по прямой (эта аксиома и дала названию метода – под «следом» понимается прямая
- 5. Метод следов включает три важных пункта: 1. Строится линия пересечения (след) секущей плоскости с плоскостью основания
- 6. Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой,
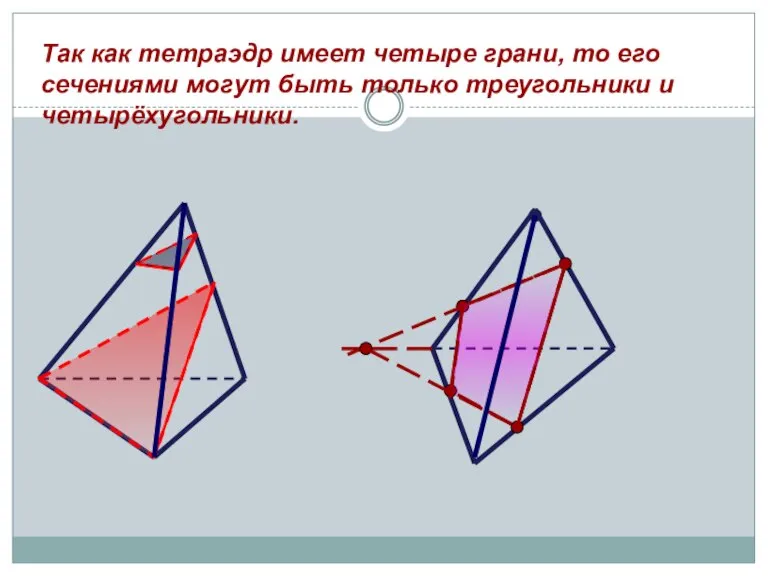
- 7. Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
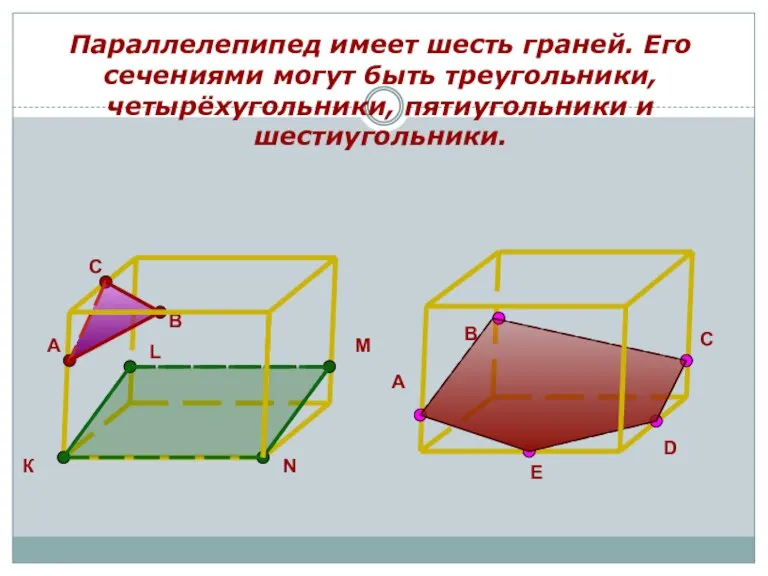
- 8. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники. А В С
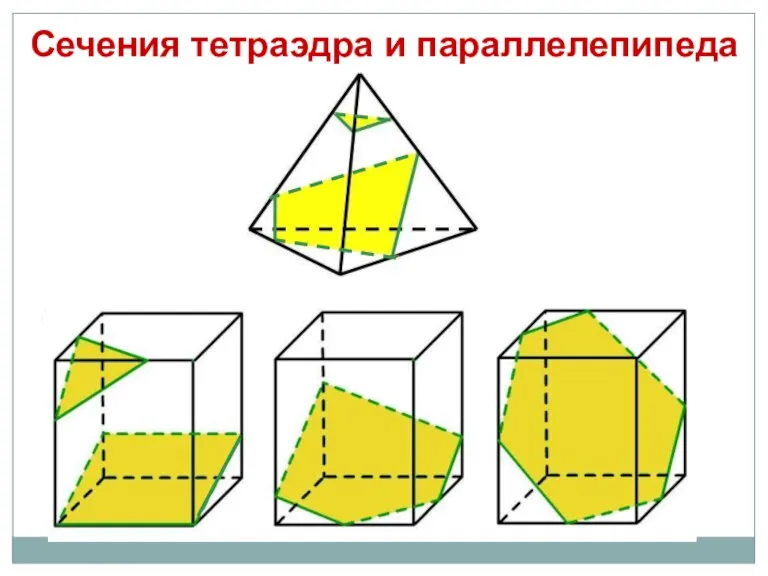
- 9. Сечения тетраэдра и параллелепипеда
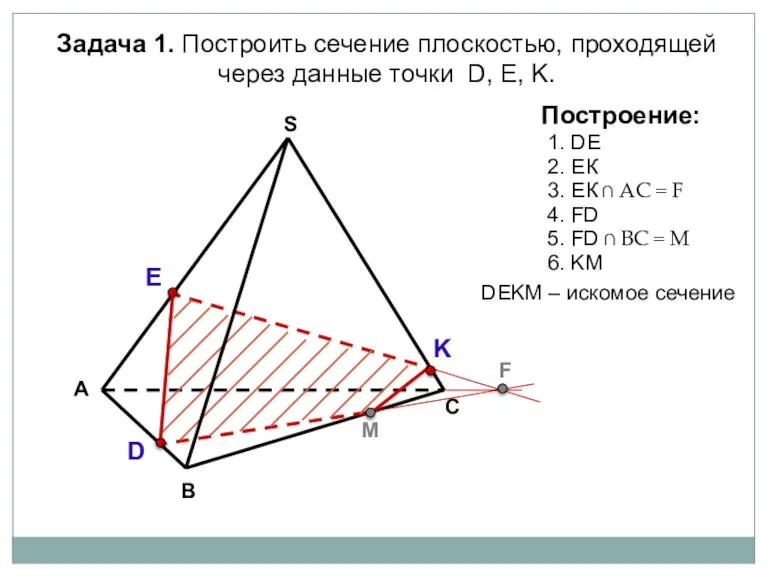
- 10. А В С S Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K.
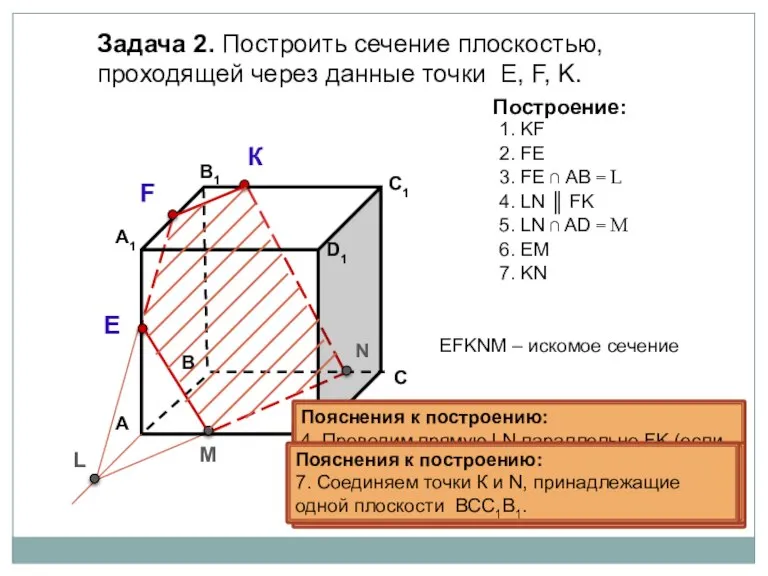
- 11. Пояснения к построению: 1. Соединяем точки K и F, принадлежащие одной плоскости А1В1С1D1. Задача 2. Построить
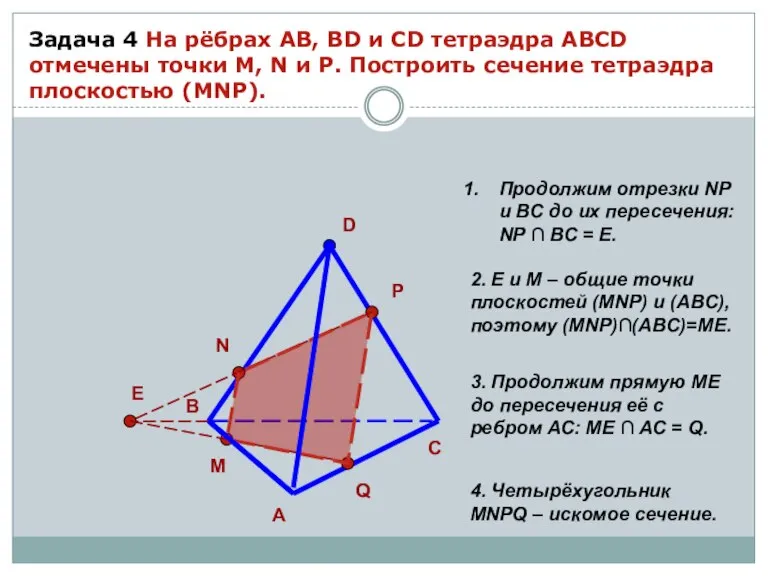
- 12. Задача 4 На рёбрах AB, BD и CD тетраэдра ABCD отмечены точки M, N и P.
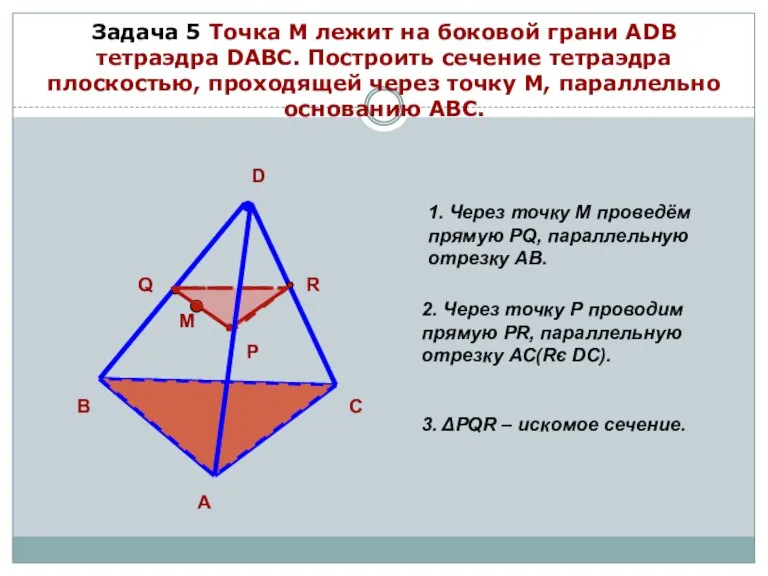
- 13. Задача 5 Точка М лежит на боковой грани АDВ тетраэдра DАВС. Построить сечение тетраэдра плоскостью, проходящей
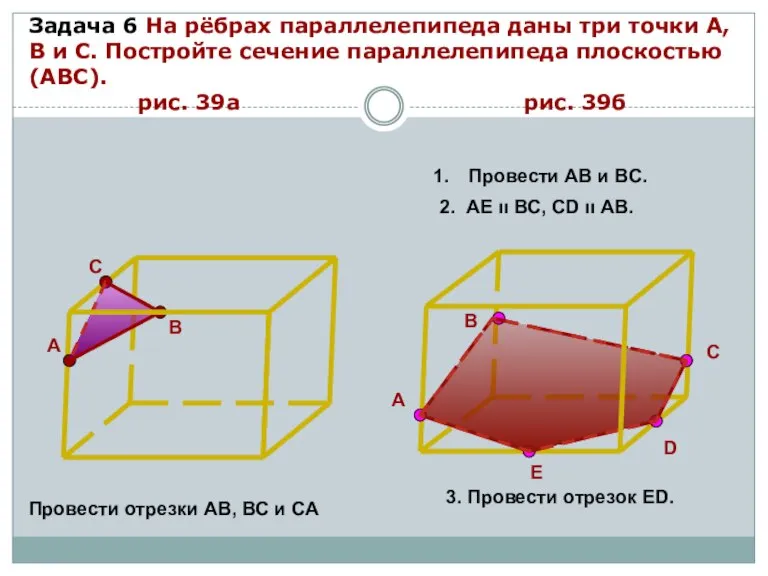
- 14. Задача 6 На рёбрах параллелепипеда даны три точки А, В и С. Постройте сечение параллелепипеда плоскостью
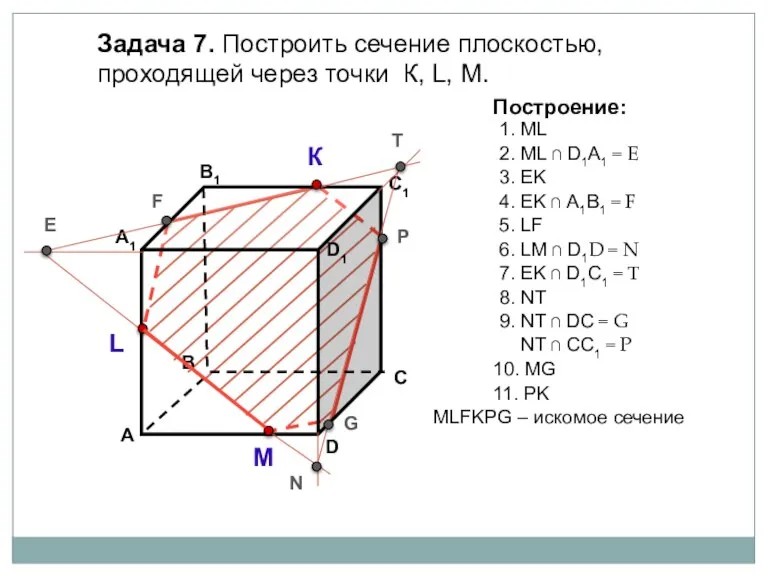
- 15. Задача 7. Построить сечение плоскостью, проходящей через точки К, L, М. К L М Построение: 1.
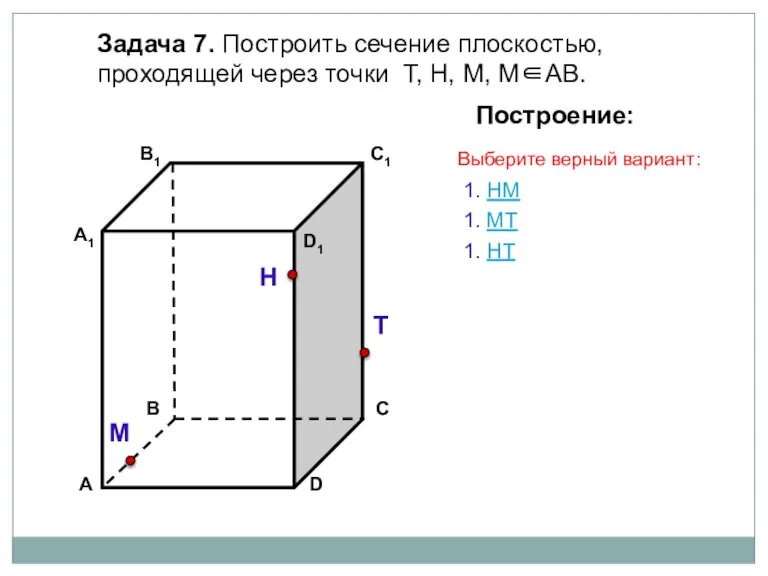
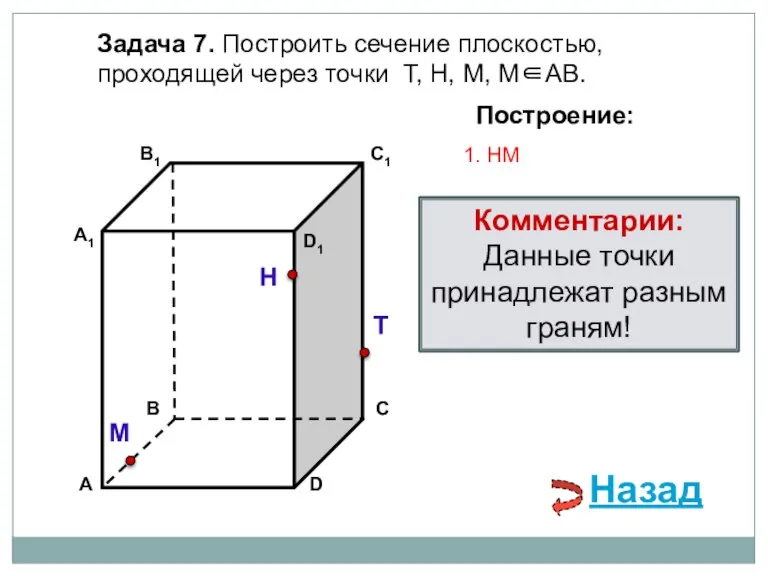
- 16. Задача 7. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
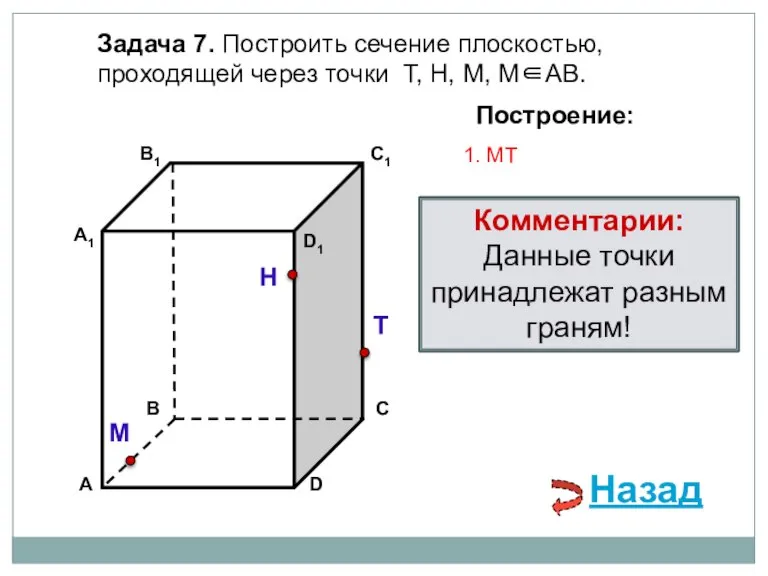
- 17. Задача 7. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
- 18. Задача 7. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
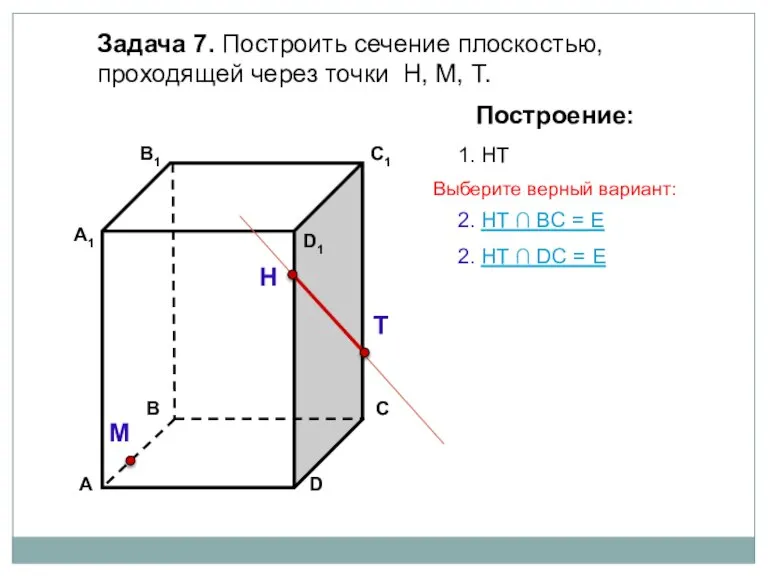
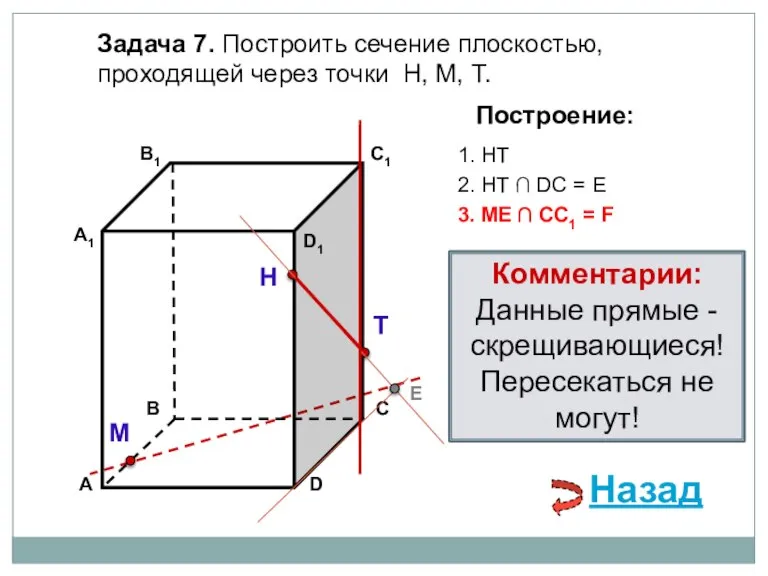
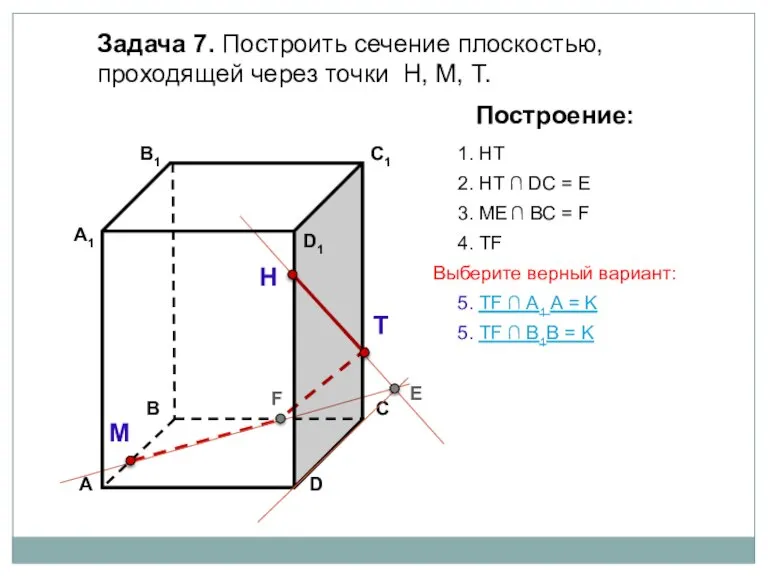
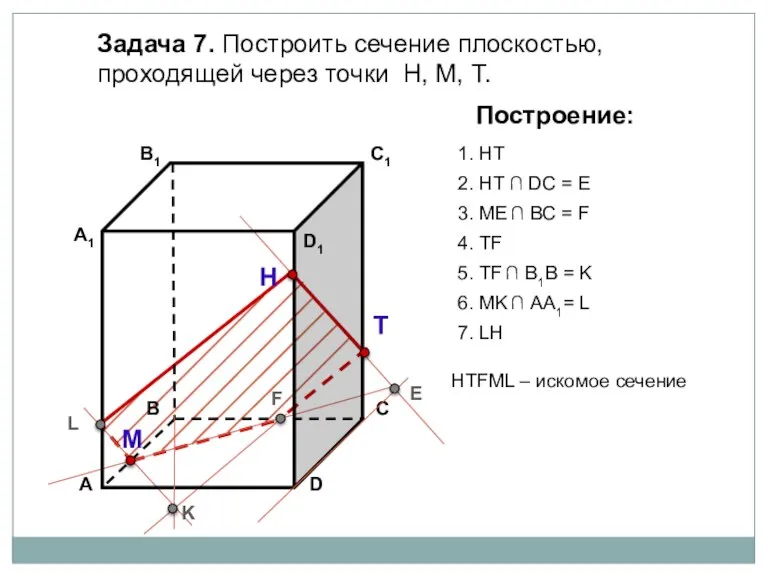
- 19. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 20. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
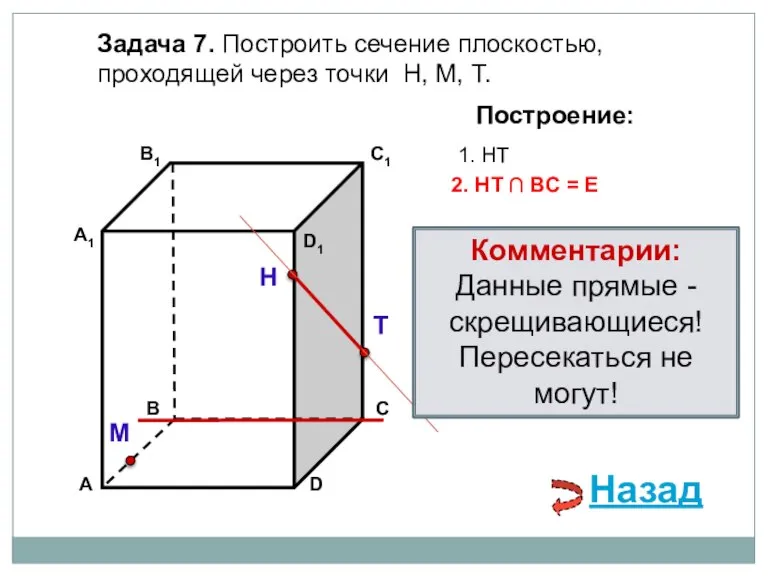
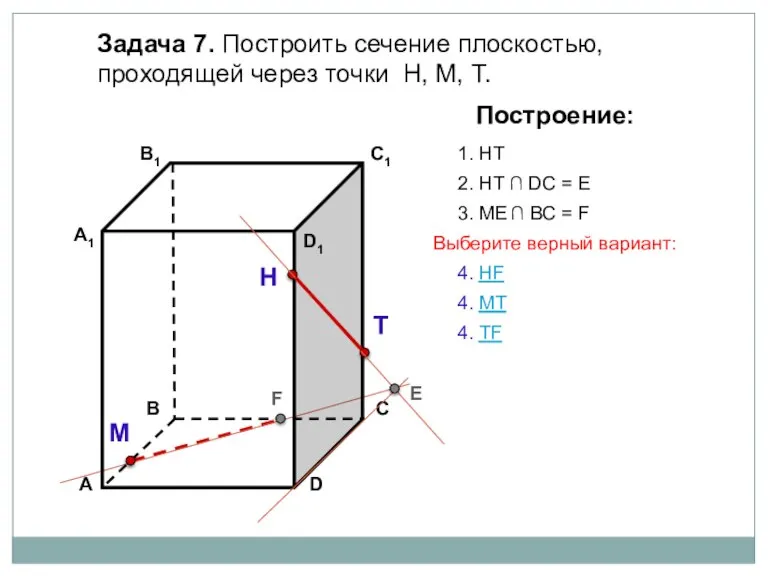
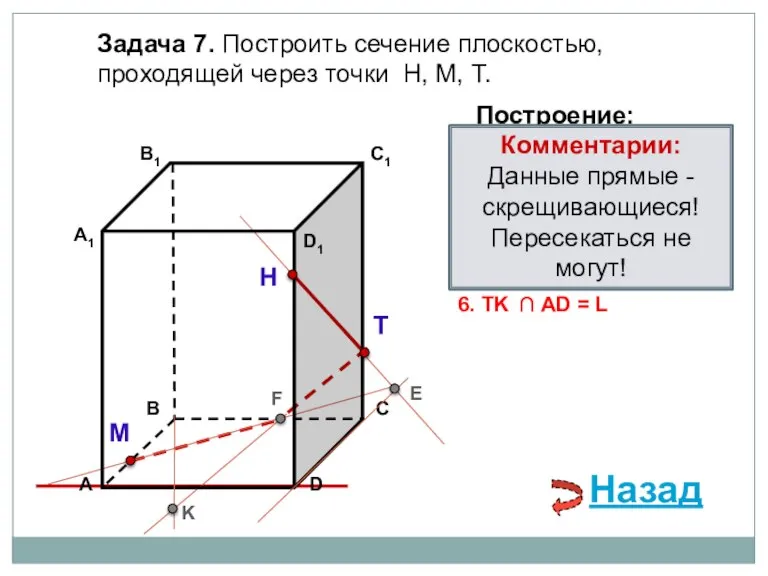
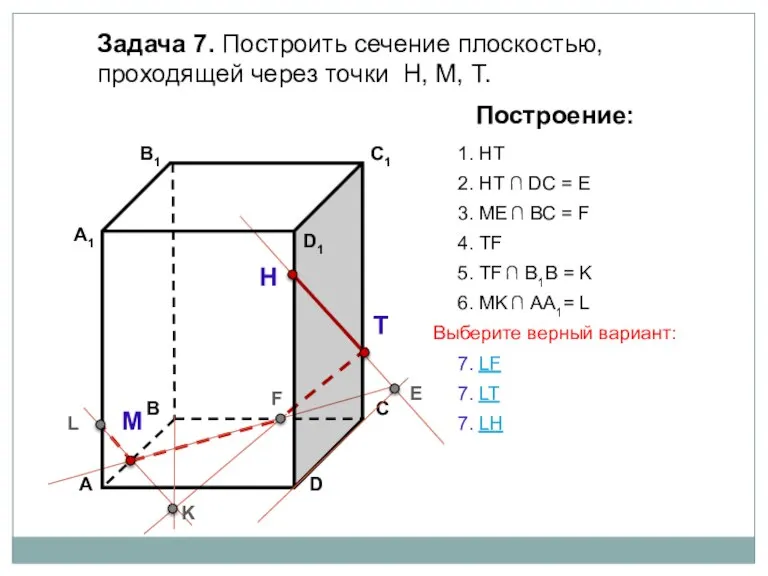
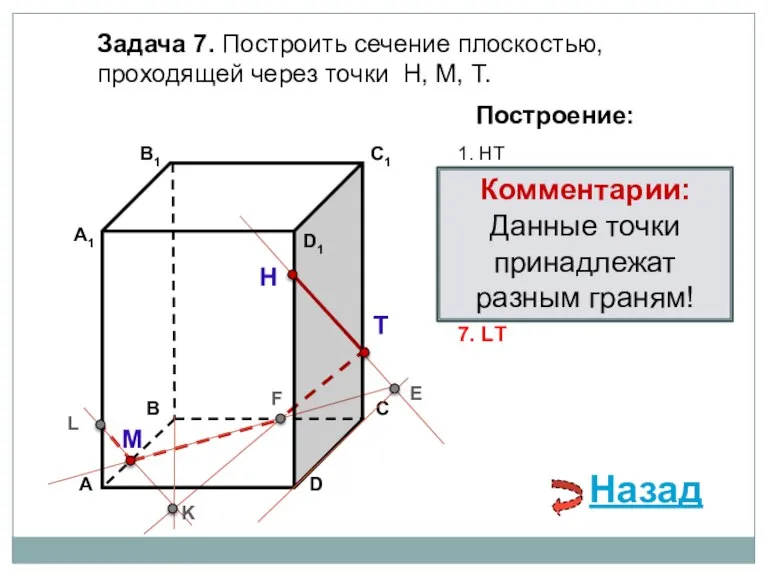
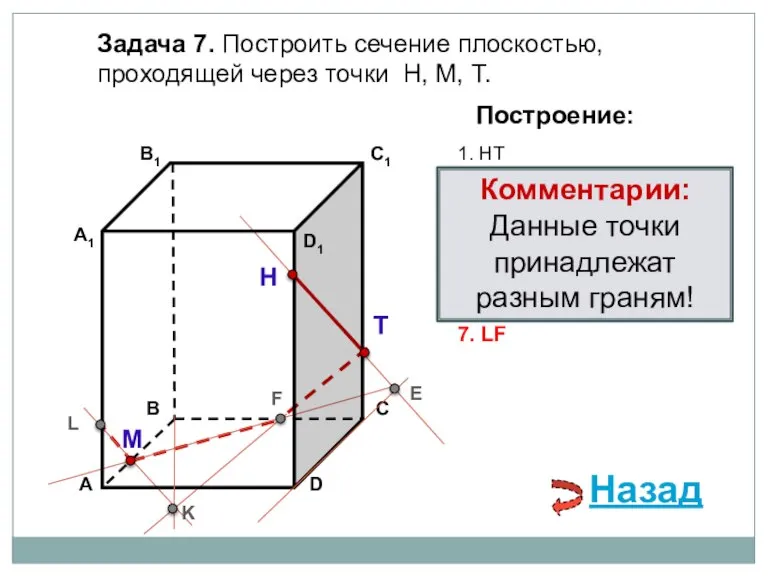
- 21. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
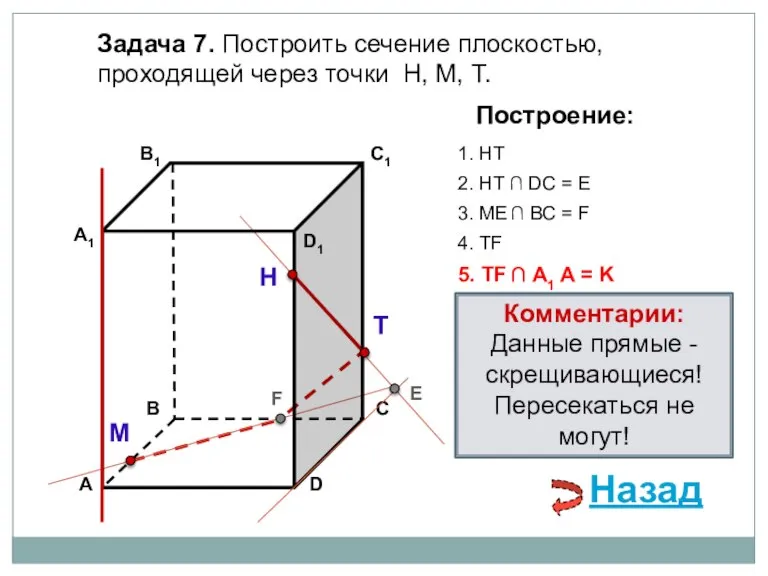
- 22. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
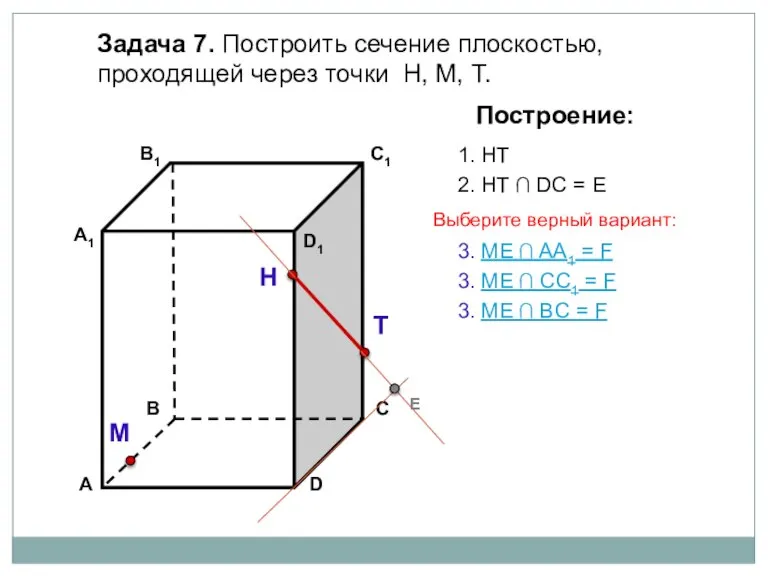
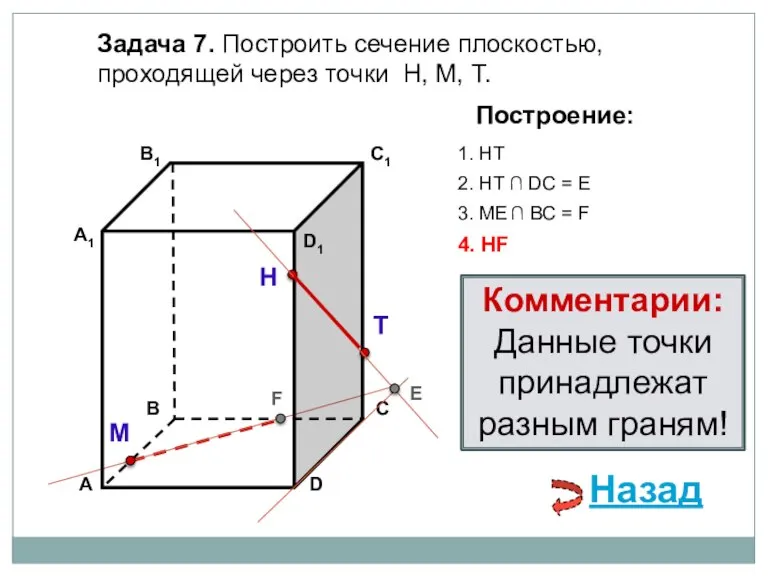
- 23. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 24. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
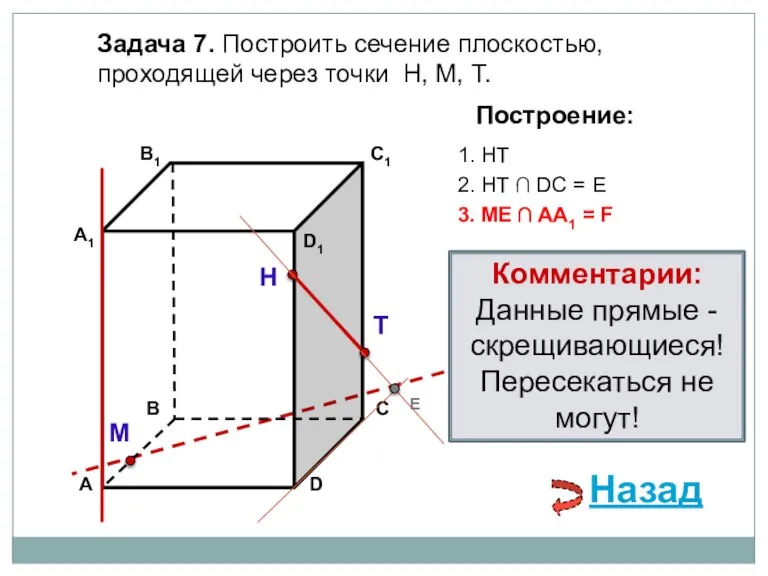
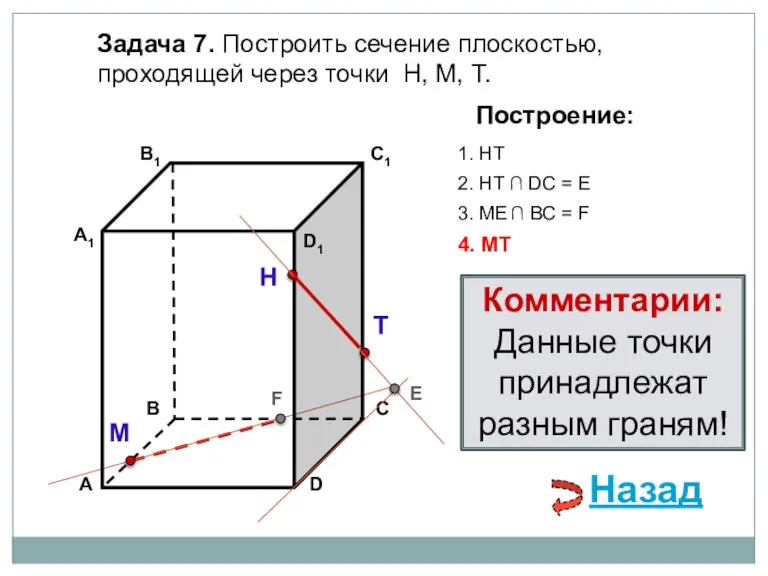
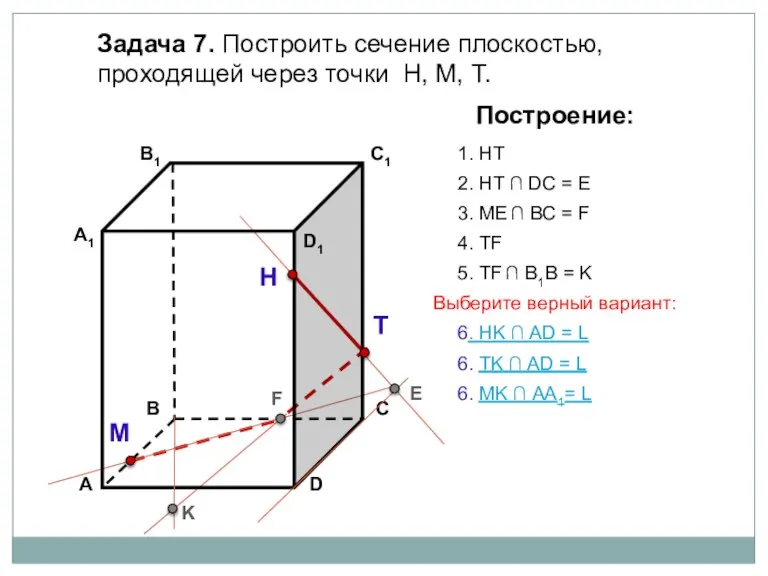
- 25. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 26. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 27. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
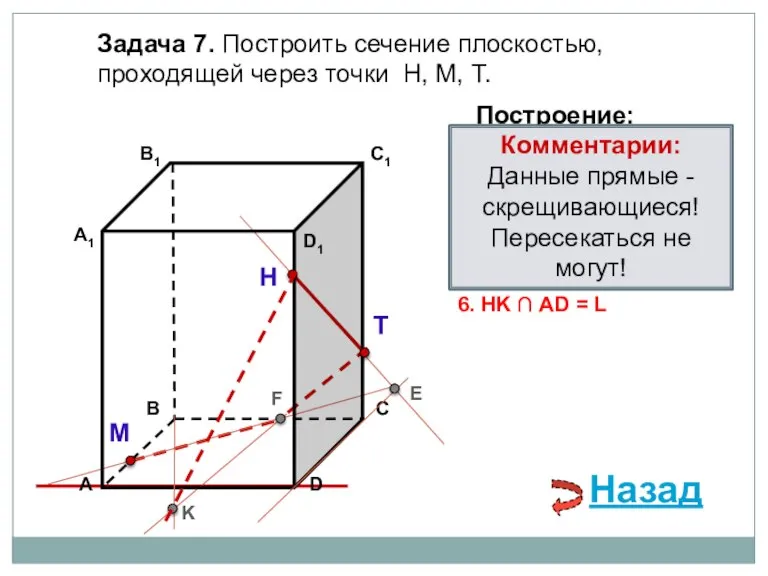
- 28. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 29. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 30. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 31. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 32. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 33. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 34. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 35. Задача 7. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
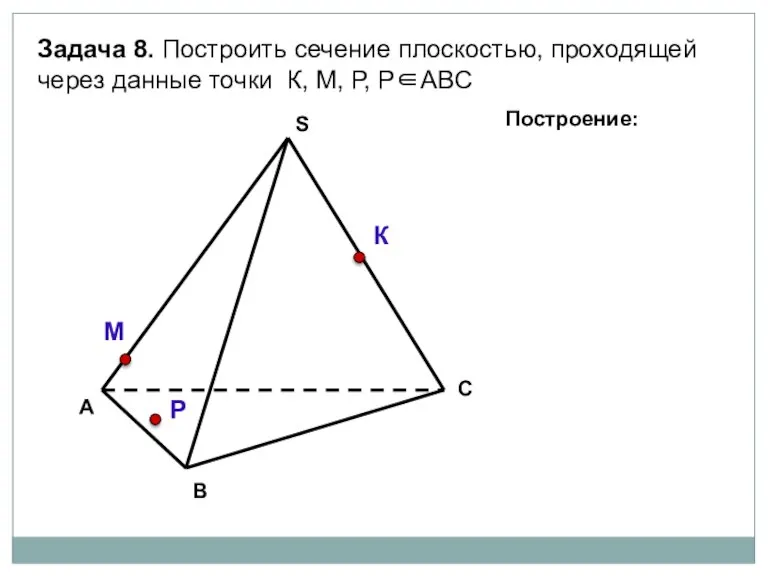
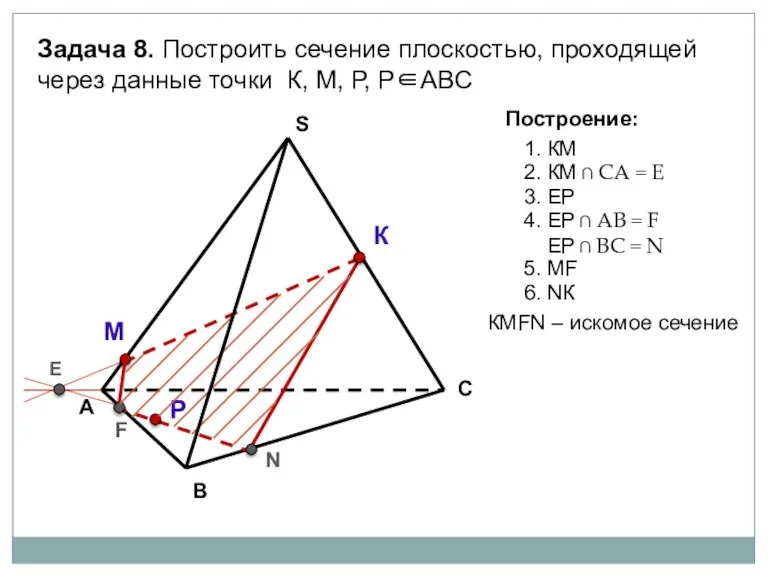
- 36. А В С S Задача 8. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 37. А В С S Задача 8. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 39. Скачать презентацию





 Решение задач
Решение задач Устный счёт. Для 5 коррекционного класса VIII вида
Устный счёт. Для 5 коррекционного класса VIII вида Основы логики
Основы логики Гамильтоновы цепи в некоторых типах линейно-выпуклых графов
Гамильтоновы цепи в некоторых типах линейно-выпуклых графов Интересные факты в тригонометрии
Интересные факты в тригонометрии Тест Смешанные числа
Тест Смешанные числа Треугольник и его виды
Треугольник и его виды Применение математики в банковском деле
Применение математики в банковском деле Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Каков развивающий потенциал функциональной линии в курсе математики?
Каков развивающий потенциал функциональной линии в курсе математики? Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ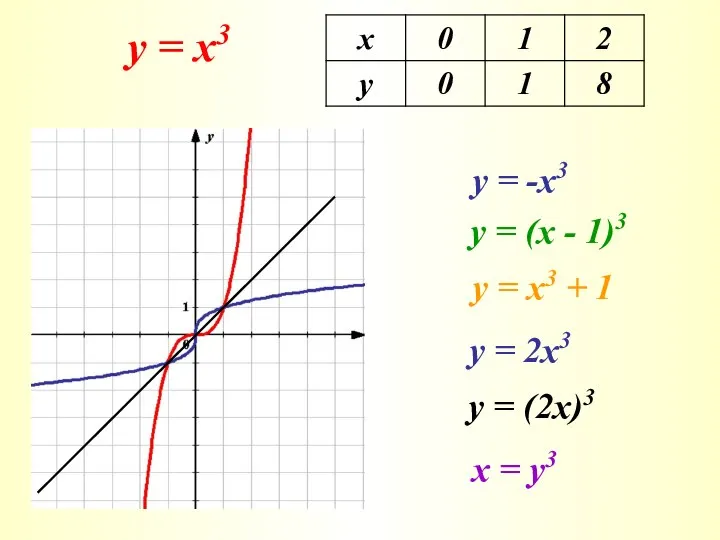 Логарифмические функции
Логарифмические функции Многоугольники в жизни
Многоугольники в жизни Алгебра в нашей жизни
Алгебра в нашей жизни Багдадская математическая школа
Багдадская математическая школа Основы теории графов
Основы теории графов Презентация на тему Свойства степени с рациональным показателем
Презентация на тему Свойства степени с рациональным показателем  Тригонометрические функции
Тригонометрические функции Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Деление с остатком
Деление с остатком Решение примеров
Решение примеров Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Решение неравенств с одной переменной. 8 класс
Решение неравенств с одной переменной. 8 класс Параллельный перенос
Параллельный перенос Подготовка к контрольной работе
Подготовка к контрольной работе Линейные уравнения. Ярмарка по решению старинных русских задач
Линейные уравнения. Ярмарка по решению старинных русских задач Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений