Элементы комбинаторики

План занятия
Перестановки (определение).
Формула числа перестановок из n элементов.
Факториал.
Решение задач.

Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Определение

Пусть имеются три книги. Обозначим их буквами
a, b и с. Эти книги можно расставить на полке по-разному.
Если первой поставить книгу a, то возможны такие расположения книг: abc, acb.
Если первой поставить книгу b, то возможными являются такие расположения: bac, bca.
И наконец, если первой поставить книгу с, то получим такие расположения: cab, cba.
Каждое из этих расположений называют
перестановкой из трёх элементов.
Пример.

Определение
Перестановкой из n элементов называется каждое расположение этих элементов в определённом порядке.
Число перестановок из n элементов обозначают символом
(читается «Р из n»).

Пусть мы имеем n элементов.
На первое место можно поставить любой из них.
Для каждого выбора первого элемента на второе место можно поставить один из оставшихся n-1 элементов.
Для каждого выбора первых двух элементов на третье место можно поставить один из оставшихся
n-2 элементов и т.д.
В результате получим, что
Рn= n (n - 1) ( n – 2) …3·2·1= n!
(читается «n факториал»).
Например, 2!= 2·1=2; 5!=5·4·3·2·1=120.
По определению считают, что 1!=1.

Таким образом, число всевозможных перестановок из
n элементов вычисляется по формуле:
= n!= 1·2·3·…·(n-2)(n-1)n

Пример 1.
Сколькими способами могут быть расставлены 8 участников финального забега на восьми беговых дорожках?

Решение.
Число способов равно числу перестановок из 8 элементов.
По формуле числа перестановок находим, что
P8=8!=1·2·3·4·5·6·7·8= 40 320.
Значит, существует 40 320 способов расстановки участников забега на восьми беговых дорожках.

Пример 2.
Сколько различных четырёхзначных чисел,
в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?

Решение.
Из цифр 0, 2, 4, 6 можно получить Р4 перестановок. Из этого числа надо исключить те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с цифры 0. Число таких перестановок равно Р3. Значит, искомое число четырёхзначных чисел (без повторения цифр), которые можно составить из цифр 0, 2, 4, 6, равно
Р4 - Р3 = 4! – 3! = 24 – 6 = 18.

Пример3.
Имеется девять различных книг, четыре из которых – учебники.
Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?

Решение.
Сначала будем рассматривать учебники как одну книгу. Тогда на полке надо расставить не девять, а шесть книг. Это можно сделать Р6 способами. В каждой из полученных комбинаций можно выполнить Р4 перестановок учебников. Значит, искомое число способов расположения книг на полке равно произведению Р6 · Р4. Получаем:
Р6 · Р4 = 6! · 4! = = 17 280.

Задачи на закрепление пройденного материала.
Сколькими способами могут встать в очередь в билетную кассу: 1) 3 человека; 2) 5 человек?
Сколько существует вариантов рассаживания вокруг стола: 1) 6 гостей на 6 стульях; 2) 7 гостей на 7 стульях?
Сколькими способами можно с помощью букв K, L, M и N обозначить вершины четырехугольника?
Сколько различных пятизначных чисел, все цифры которых различны, можно записать с помощью цифр 4, 5, 6, 7 и 8?
Сколькими способами можно расставить на полке 8 книг, среди которых 2 книги одного автора, которые при любых перестановках должны стоять рядом?
В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом?

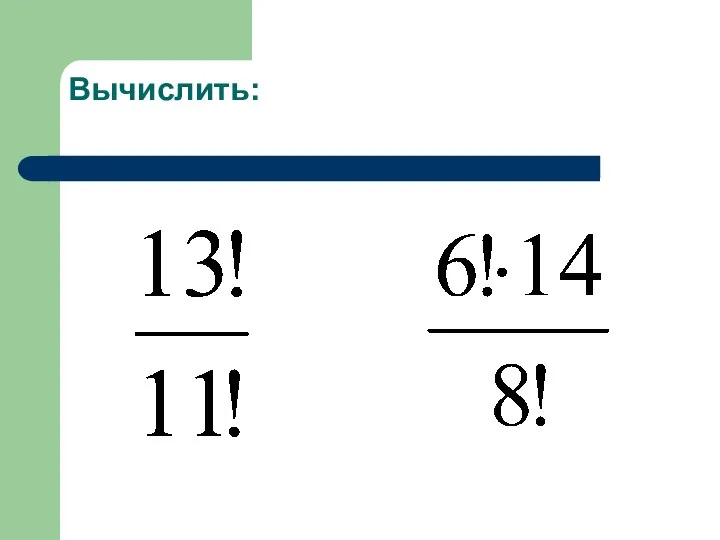
Вычислить: