Содержание
- 2. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax²+bx+c, где х - независимая
- 3. Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или вниз (если а у=2х²+4х-1 –
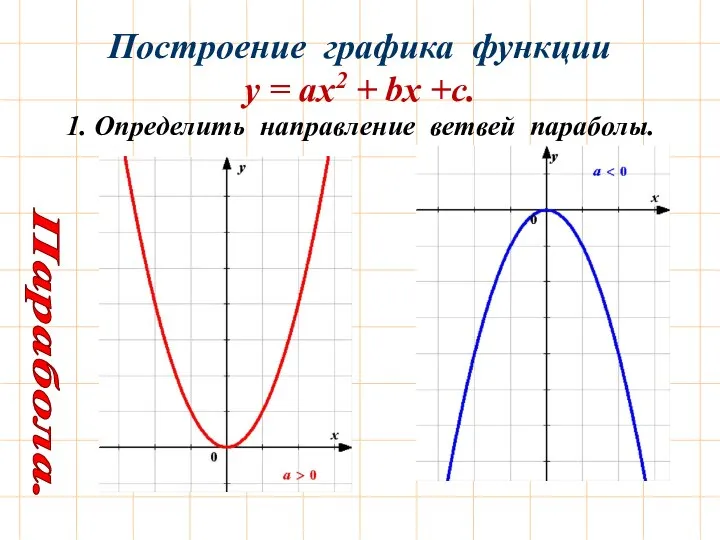
- 4. Построение графика функции у = ах2 + bх +с. 1. Определить направление ветвей параболы. Парабола.
- 5. 2. Найти координаты вершины параболы (х0; у0). 3. Провести ось симметрии. (х0;у0)
- 6. 4. Определить точки пересечения графика функции с осью Ох, т.е. найти нули функции при у =
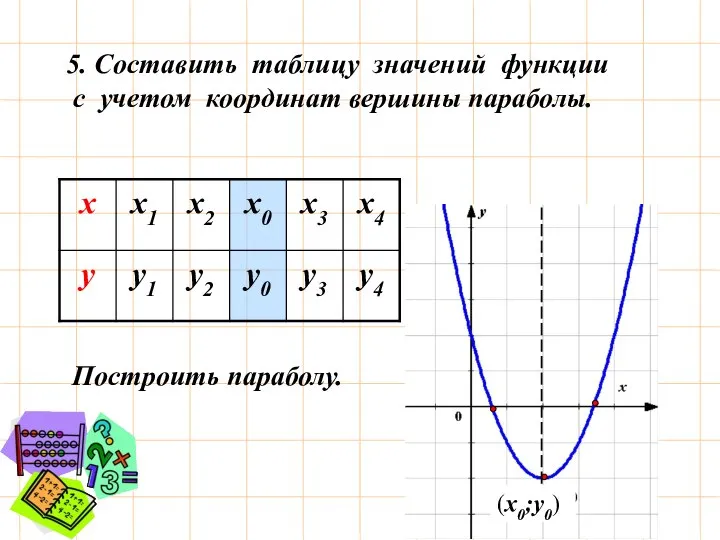
- 7. 5. Составить таблицу значений функции с учетом координат вершины параболы. Построить параболу. (х0;у0)
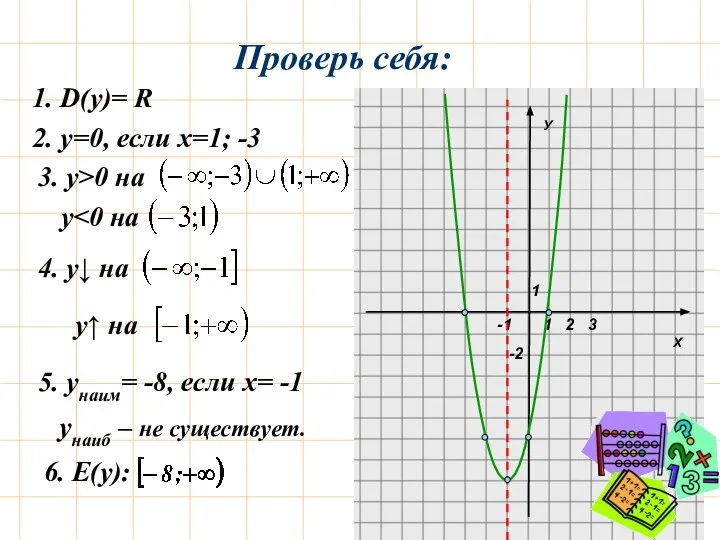
- 8. Постройте график функции у=2х²+4х-6, опишите его свойства
- 9. Х У 1 1 -2 2 3 -1 1. D(y)= R 2. у=0, если х=1; -3
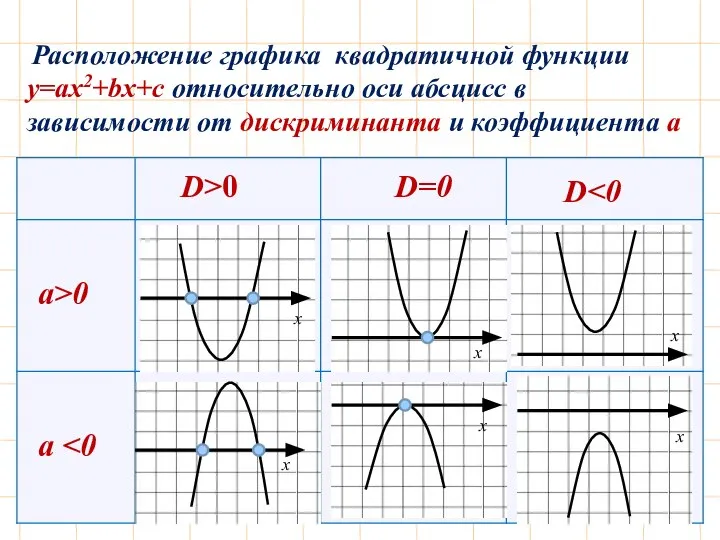
- 10. D>0 D=0 D а>0 а Расположение графика квадратичной функции у=aх2+bx+c относительно оси абсцисс в зависимости от
- 12. Скачать презентацию





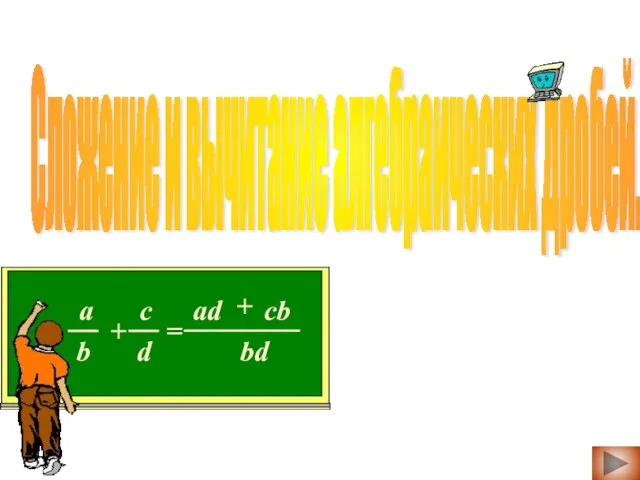 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА
Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА  Действительные числа
Действительные числа Математика в здоровье человека
Математика в здоровье человека Длина окружности
Длина окружности Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства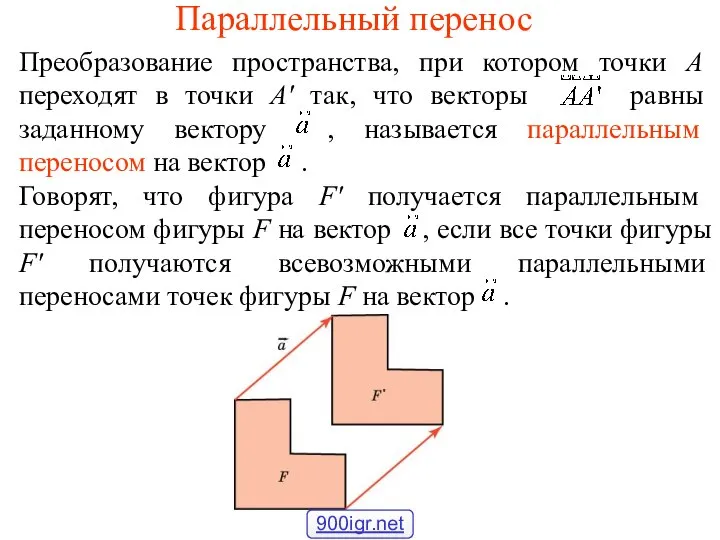 Параллельный перенос
Параллельный перенос Арифметическая прогрессия
Арифметическая прогрессия Метод Гаусса
Метод Гаусса Аттестационная работа. Элективный кружок, как элемент проектной деятельности
Аттестационная работа. Элективный кружок, как элемент проектной деятельности Презентация на тему Десяток (1 класс)
Презентация на тему Десяток (1 класс)  Преобразование буквенных выражений. Правила математического синтаксиса
Преобразование буквенных выражений. Правила математического синтаксиса Решение задач с помощью дифференциальных уравнений
Решение задач с помощью дифференциальных уравнений Первый признак равенства треугольников
Первый признак равенства треугольников Третий признак равенства треугольников. Математический диктант
Третий признак равенства треугольников. Математический диктант Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни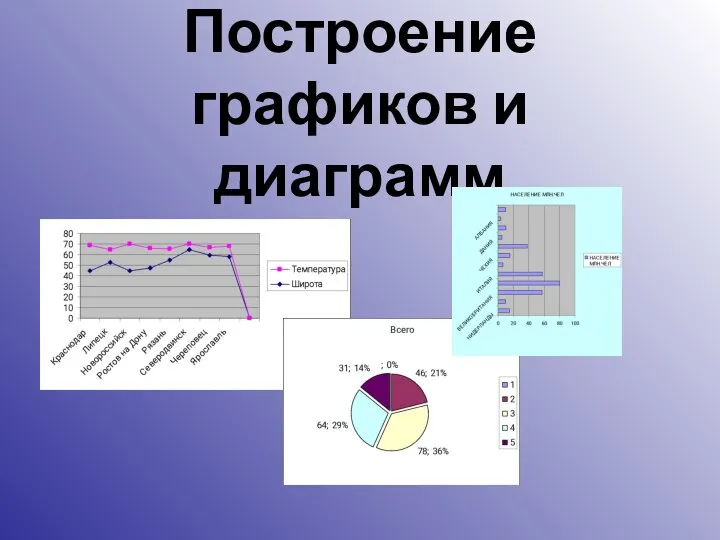 Электронные таблицы. Построение графиков и диаграмм
Электронные таблицы. Построение графиков и диаграмм Задача про комбинацию окружностей и квадрата и её обобщение от Тимофея Гаврикова
Задача про комбинацию окружностей и квадрата и её обобщение от Тимофея Гаврикова Отбор корней в тригонометрическом уравнении
Отбор корней в тригонометрическом уравнении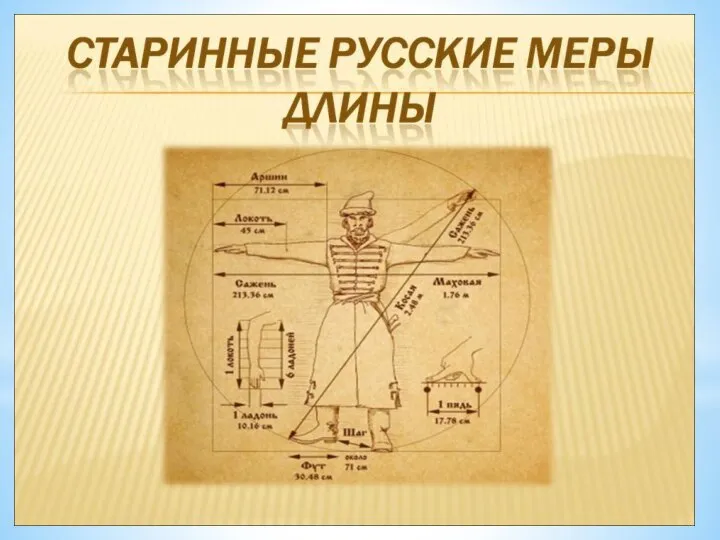 Старинные русские меры
Старинные русские меры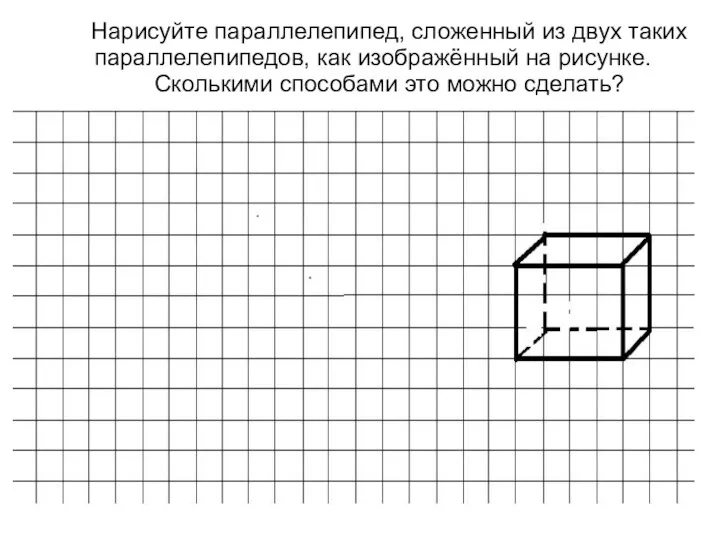 Многогранники. 5 класс
Многогранники. 5 класс Описанная окружность. Задачи
Описанная окружность. Задачи Геометрическая прогрессия
Геометрическая прогрессия Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Занятие 1_2022
Занятие 1_2022 Параллелограмм
Параллелограмм Интегральное исчисление
Интегральное исчисление Критерий Пирсона
Критерий Пирсона