ЛЕКЦИЯ_6

п.1. Метод координат на плоскости.
Суть метода: замена геометрических понятий и фактов алгебраическими соотношениями через координаты.

Основные формулы
1) Расстояние между двумя точками на плоскости.

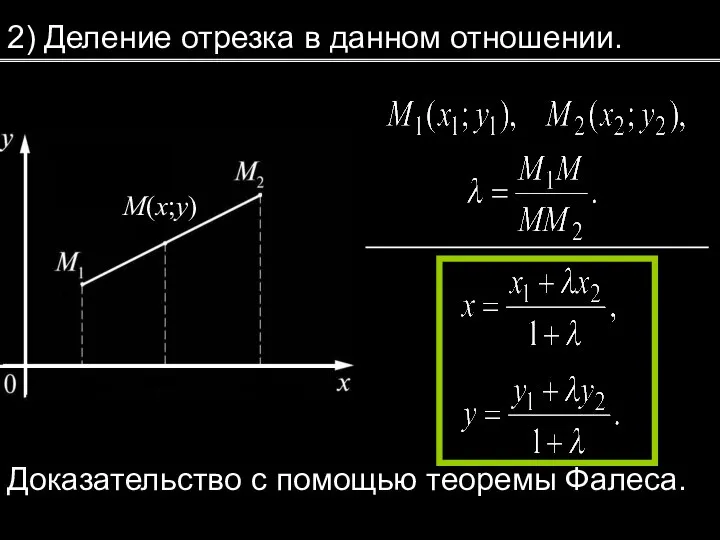
2) Деление отрезка в данном отношении.
M(x;y)
Доказательство с помощью теоремы Фалеса.

Если т.е. M ─ середина отрезка
то

п.2. Уравнение линии.
Уравнение
связывающее x и y, называется уравнением некоторой линии L,
связывающее x и y, называется уравнением некоторой линии L, если этому уравнению удовлетворяют координаты любой точки, лежащей на линии L,
связывающее x и y, называется уравнением некоторой линии L, если этому уравнению удовлетворяют координаты любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на L.

Замечание 1.
Замечание 1. Чтобы определить, принадлежит ли некоторая точка заданной линии ,
Замечание 1. Чтобы определить, принадлежит ли некоторая точка заданной линии , следует подставить координаты точки в уравнение линии .
Если , то M принадлежит L, иначе M не принадлежит L.

Пример. Определите, лежит ли точка на окружности
Решение. Так как
то M не лежит на данной окружности.

Замечание 2.
Замечание 2. Чтобы определить координаты точки пересечения двух линий и ,
Замечание 2. Чтобы определить координаты точки пересечения двух линий и , следует решить систему уравнений:

Пример. Найти количество точек пересечения прямой и окружности
Решение. Решим систему уравнений
Т.к. D>0, то система имеет два решения, т.е. линии пересекаются в двух точках.

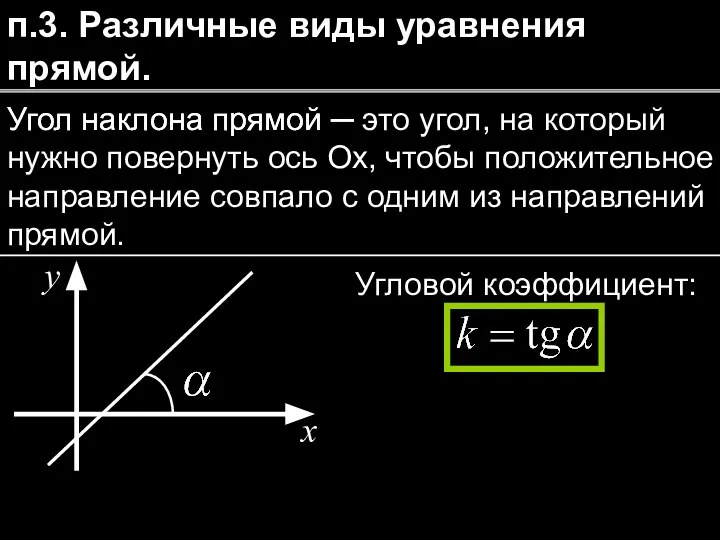
п.3. Различные виды уравнения прямой.
Угол наклона прямой ─
Угол наклона прямой ─ это угол, на который нужно повернуть ось Ox, чтобы положительное направление совпало с одним из направлений прямой.
Угловой коэффициент:
x
y

1) Уравнение прямой с угловым коэффициентом.

2) Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом.

3) Уравнение прямой, проходящей через две данные точки.

Замечание 1.
Если , то
Если , то

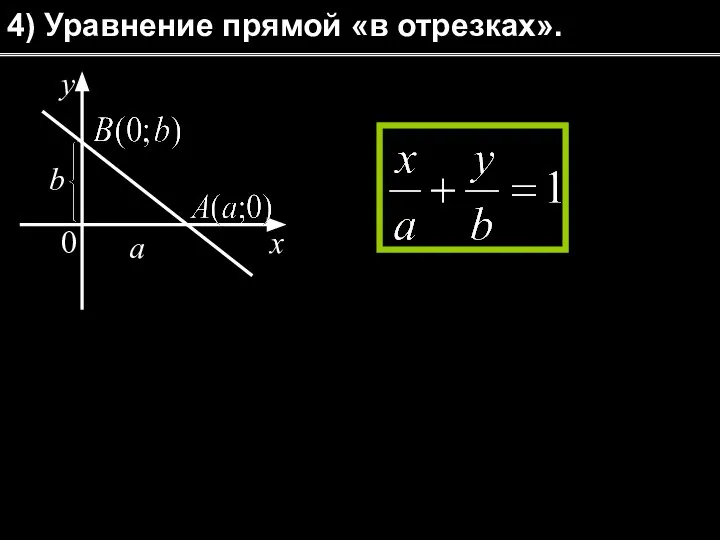
4) Уравнение прямой «в отрезках».
a
b

5) Общее уравнение прямой.
и, обратно, уравнение (1) при произвольных коэффициентах А, В, С (А и В одновременно не равны нулю) определяет некоторую прямую в прямоугольной системе координат Oxy.
Теорема. В прямоугольной системе координат любая прямая задается уравнением первой степени
(1)

Замечание 3. Вектор, параллельный данной прямой, называется направляющим вектором этой прямой.
Если прямая задана общим уравнением
то вектор
является направляющим вектором этой прямой.

Замечание 4. Вектор, перпендикулярный данной прямой, называется нормальным вектором этой прямой.
Если прямая задана общим уравнением
то вектор
является нормальным вектором этой прямой.
— уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

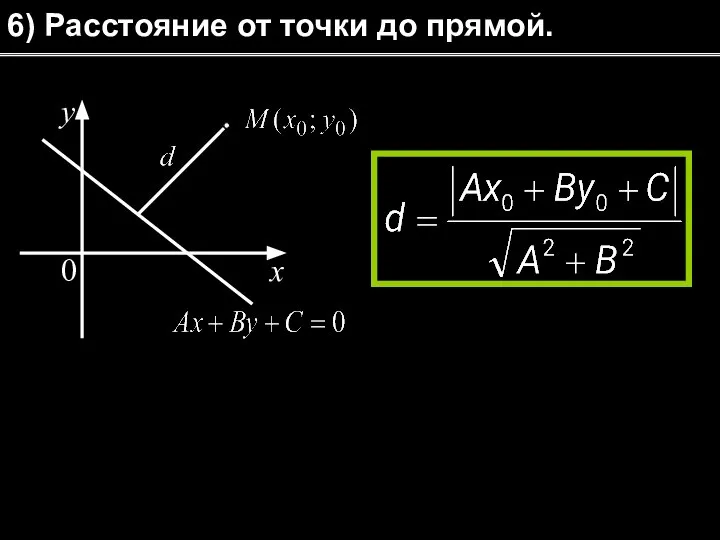
6) Расстояние от точки до прямой.

п.4. Угол между двумя прямыми на плоскости.

Угол между прямыми и ─ это угол, на который нужно повернуть против часовой стрелки прямую до совпадения с прямой
Угол между прямыми и ─

─ условие параллельности

─ условие перпендикулярности

Пример. Составить общее уравнение прямой, проходящей через точку M(3,-1) и перпендикулярной прямой
Решение.
M
1-й способ.
Учитывая условие перпендикулярности

Воспользуемся уравнение из пункта 2)
2-й способ.
Направляющий вектор прямой
является нормальным вектором прямой l.
Тогда

п.5. Взаимное расположение двух прямых на плоскости.

x
y
0
прямые пересекаются

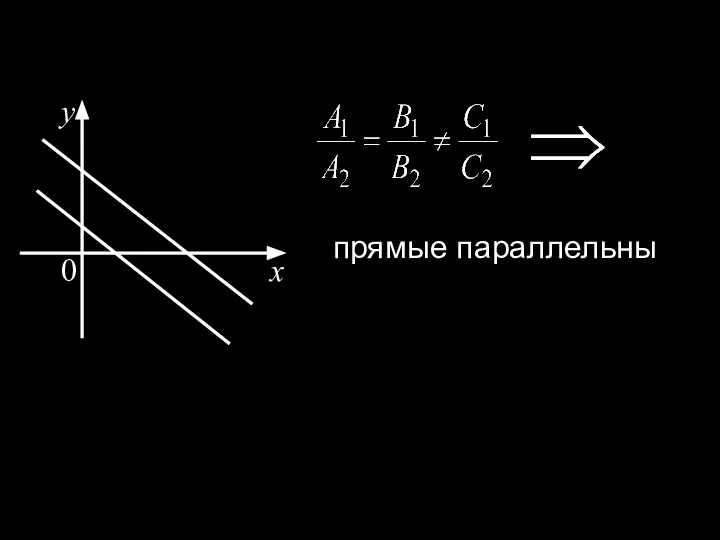
x
y
0
прямые параллельны