Содержание
- 2. Пусть элемент х можно выбрать m способами; элемент у можно выбрать K способами, тогда число всех
- 3. Пусть х – некоторое множество, состоящее из m элементов, а выборка состоит из k элементов, тогда:
- 5. Решение задач. №1.В гостинице 20 мест можно забронировать только 5 мест. Сколькими способами можно это сделать?
- 6. №4.В корзине 20 груш, 15 яблок и 10 апельсинов. Сколько имеется возможностей для выбора: а) груши
- 7. №5.На кафедре педагогики 8 преподавателей, каждый должен провести консультацию в один из 8 предложенных дней. Сколькими
- 8. №7.В корзине 5 белых и 2 черных шара. Сколько существует возможностей выбрать 3 белых и 1
- 10. Скачать презентацию







 МВ УРОК 22 ГЕО ТРЕУГОЛЬНИК
МВ УРОК 22 ГЕО ТРЕУГОЛЬНИК Четырехзначные числа
Четырехзначные числа Уравнения с двумя переменными
Уравнения с двумя переменными Решение задач на межпредметные связи
Решение задач на межпредметные связи От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Презентация на тему Длиннее короче
Презентация на тему Длиннее короче  Графики кусочных функций
Графики кусочных функций Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Степень и ее свойства
Степень и ее свойства Кругові приклади
Кругові приклади Величины. Свойства величин
Величины. Свойства величин Многонранники в нашей жизни
Многонранники в нашей жизни Куб
Куб Подготовка к ЕГЭ. Повторение. Математика
Подготовка к ЕГЭ. Повторение. Математика Косинус угла
Косинус угла Занимательная геометрия
Занимательная геометрия Сближение меридианов. Международное геомагнитное аналитическое поле IGRF
Сближение меридианов. Международное геомагнитное аналитическое поле IGRF Понятие цилиндра
Понятие цилиндра Измерение площадей. Площадь прямоугольника
Измерение площадей. Площадь прямоугольника Teorema_polnoy_veroyatnosti
Teorema_polnoy_veroyatnosti Приближение десятичных дробей
Приближение десятичных дробей Особенности набора математических формул в Microsoft
Особенности набора математических формул в Microsoft Презентация на тему Решето Эратосфена
Презентация на тему Решето Эратосфена  Обратные тригонометрические функции
Обратные тригонометрические функции tema_2_1_metrologia (1)
tema_2_1_metrologia (1) Числовая последовательность
Числовая последовательность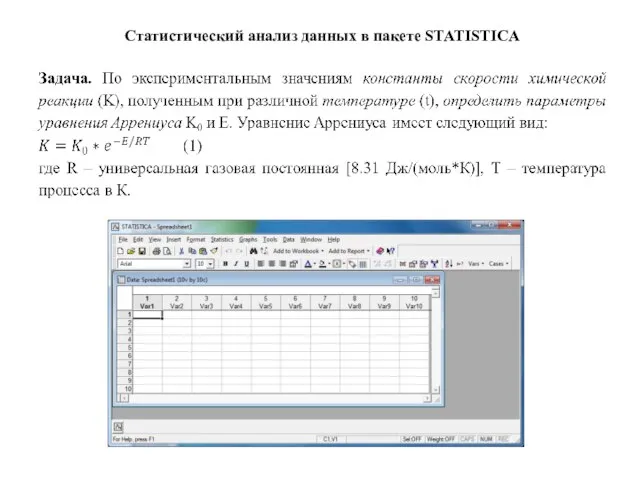 Статистический анализ данных в пакете Statistica
Статистический анализ данных в пакете Statistica Игра
Игра