Числовая последовательность

Понятие числовой последовательности
Рассмотрим ряд натуральных чисел N:
1, 2, 3, …, n – 1, n, п + 1, …
Функцию y = f(x), x ∈ N называют функцией натурального аргумента или числовой последовательностью и обозначают y = f(n) или y1, y2, …, yn, … или {уn}.
Величина уn называется общим членом последовательности.
Обычно числовая последовательность задаётся некоторой формулой уn = f(n), позволяющей найти любой член последовательности по его номеру n;
эта формула называется формулой общего члена.

Примеры числовых последовательностей
1, 2, 3, 4, 5, … – ряд натуральных чисел;
2, 4, 6, 8, 10, … – ряд чётных чисел;
1, 4, 9, 16, 25, … – ряд квадратов натуральных чисел;
5, 10, 15, 20, … – ряд натуральных чисел, кратных 5;
1, 1/2, 1/3, 1/4, 1/5, ... – ряд вида 1/n, где n∈N;
и т.д.

Способы задания последовательностей
Перечислением членов последовательности (словесно).
Заданием аналитической формулы.
Заданием рекуррентной формулы.
Примеры:
Последовательность простых чисел:
2; 3; 5; 7; 11; 13; 17; 19; 23; 29; …
Арифметическая прогрессия:
an = a1 + (n – 1)d
Геометрическая прогрессия:
bn + 1 = bn ∙ q

Ограниченность числовой последовательности
Последовательность {уn} называют ограниченной сверху, если все ее члены не больше некоторого числа.
Пример: -1, -4, -9, -16, …, -п2, … - ограничена сверху 0.
Последовательность {уn} ограниченна сверху, если существует число M такое, что для любого п выполняется неравенство
уп ≤ М
Число М называют верхней границей последовательности.

Ограниченность числовой последовательности
Последовательность {уn} называют ограниченной снизу, если все ее члены не меньше некоторого числа.
Пример: 1, 4, 9, 16, …, п2, … - ограничена снизу 1.
Последовательность {уn} ограниченна снизу, если существует число m такое, что для любого п выполняется неравенство
уп ≥ m
Число m называют нижней границей последовательности.
Если последовательность ограничена и сверху и снизу, то ее называют ограниченной последовательностью.

Возрастание и убывание числовой последовательности
Последовательность {уn} называют возрастающей последовательностью, если каждый ее член больше предыдущего:
у1 < y2 < y3 < y4 < … < yn < yn+1 < …
Пример: 1, 3, 5, 7, 9, 2п – 1, … - возрастающая последовательность.
Последовательность {уn} называют убывающей последовательностью, если каждый ее член меньше предыдущего:
у1 > y2 > y3 > y4 > … > yn > yn+1 > …
Пример: 1, 1/3, 1/5, 1/7, 1/(2п – 1), … - убывающая последовательность.
Возрастающие и убывающие последовательности называют монотонными

Предел числовой последовательности
Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n.
В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
Число а называется пределом числовой последовательности {un}
если для любого ε > 0 найдется такое число N = N(ε), зависящее от ε, что │un – a│< ε при n > N

Предел числовой последовательности
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого ε > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (a – ε, a + ε).
Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.

Рассмотрим последовательность:
– гармонический ряд
Если │q│< 1, то
Если │q│> 1, то последовательность уn = q n расходится
Если m∈N, k∈R, то

Свойства пределов
предел частного равен частному пределов:
предел произведения равен произведению пределов:
предел суммы равен сумме пределов:
постоянный множитель можно вынести за знак предела:

Примеры:

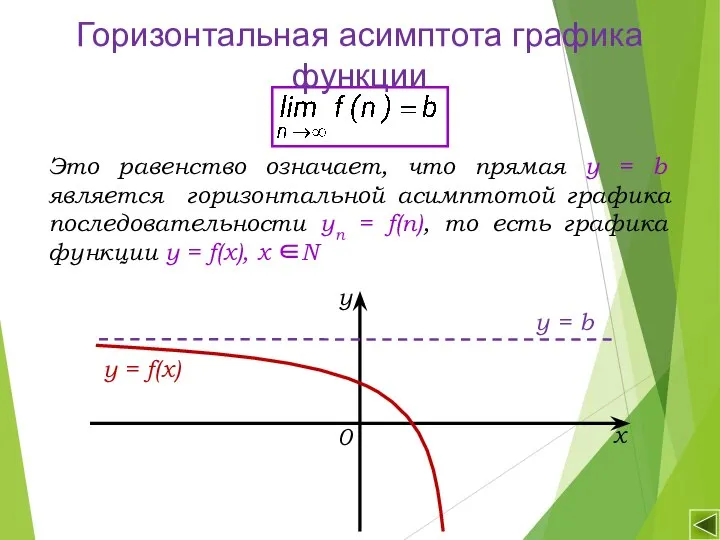
Это равенство означает, что прямая у = b является горизонтальной асимптотой графика последовательности yn = f(n), то есть графика функции y = f(х), х ∈N
Горизонтальная асимптота графика функции
х
у
y = f(x)
0
у = b

Сумма бесконечной геометрической прогрессии
Пример:
Дано: b1 + b2 + b3 + b4 + … + bn + … = 9;
(b1)2 + (b2)2 + (b3)2 + (b4)2 + … + (bn)2 + … = 40,5.
Найти: b5.
Решение:

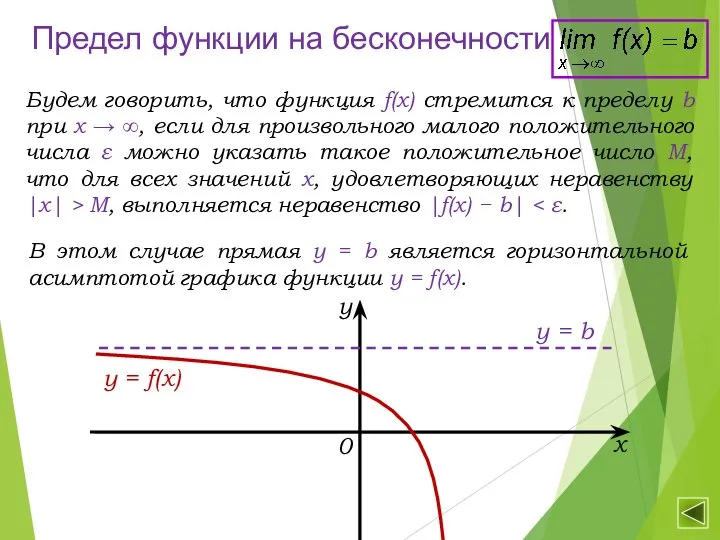
Предел функции на бесконечности
В этом случае прямая у = b является горизонтальной асимптотой графика функции y = f(x).
х
у
y = f(x)
0
у = b
Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M, что для всех значений x, удовлетворяющих неравенству |x| > M, выполняется неравенство |f(x) − b| < ε.

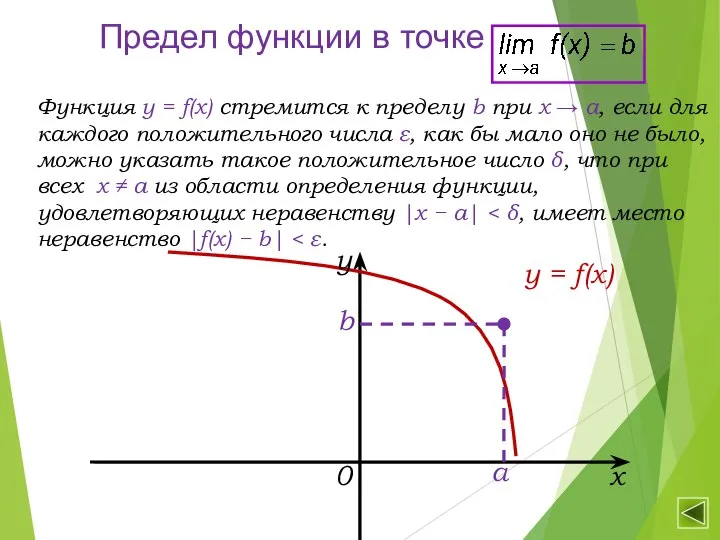
Предел функции в точке
Функция y = f(x) стремится к пределу b при x → a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x − a| < δ, имеет место неравенство |f(x) − b| < ε.
х
y = f(x)
0
b
у
а