Содержание
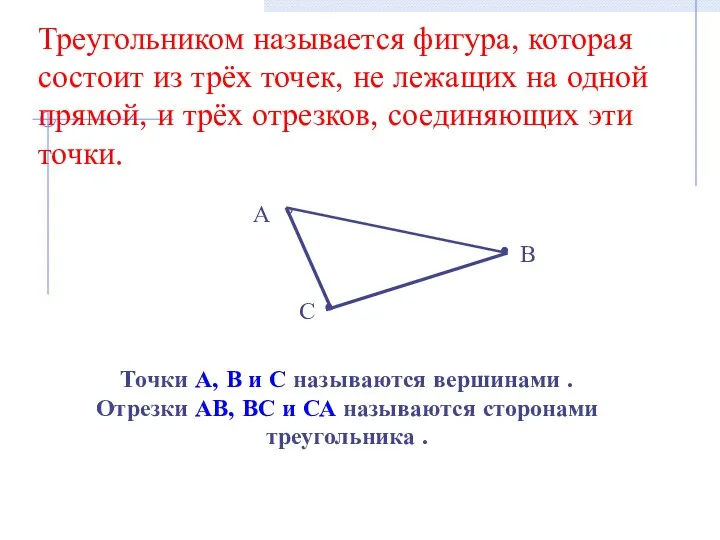
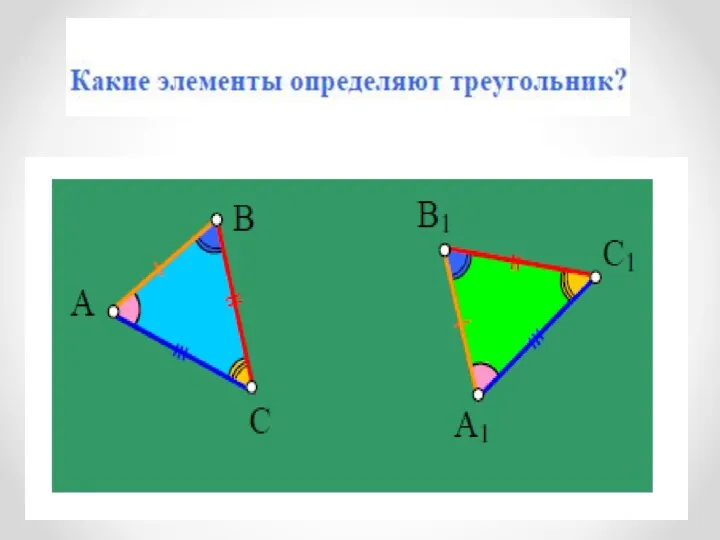
- 3. Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков,
- 5. ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ В ТРЕУГОЛЬНИКЕ 7 класс
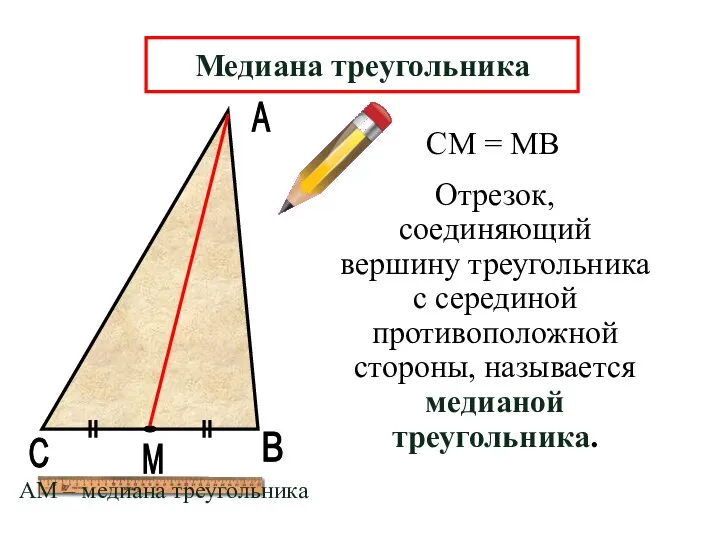
- 6. А В М Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. С СМ
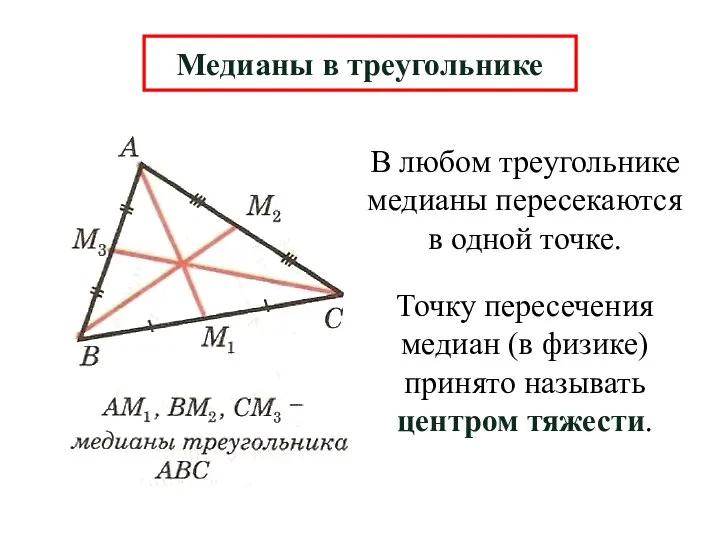
- 7. В любом треугольнике медианы пересекаются в одной точке. Медианы в треугольнике Точку пересечения медиан (в физике)
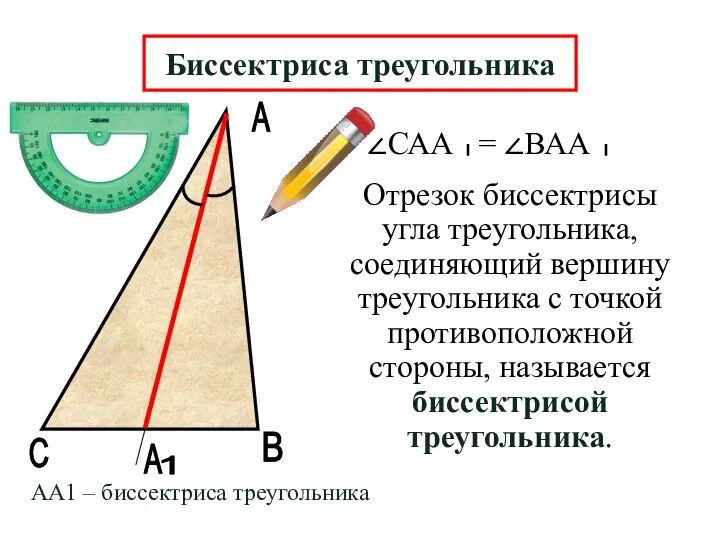
- 8. А В А Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой
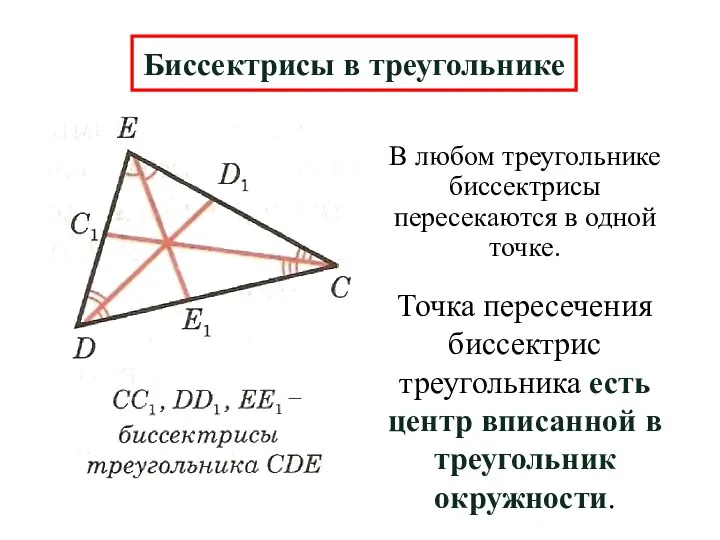
- 9. В любом треугольнике биссектрисы пересекаются в одной точке. Биссектрисы в треугольнике Точка пересечения биссектрис треугольника есть
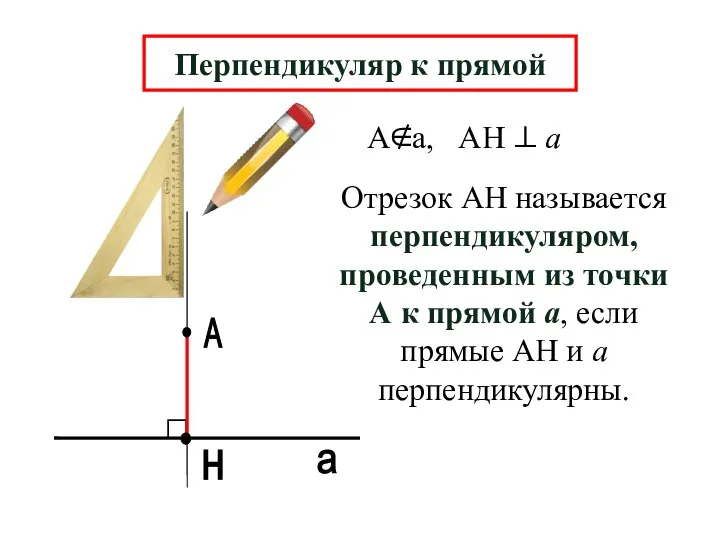
- 10. А н а Перпендикуляр к прямой Отрезок АН называется перпендикуляром, проведенным из точки А к прямой
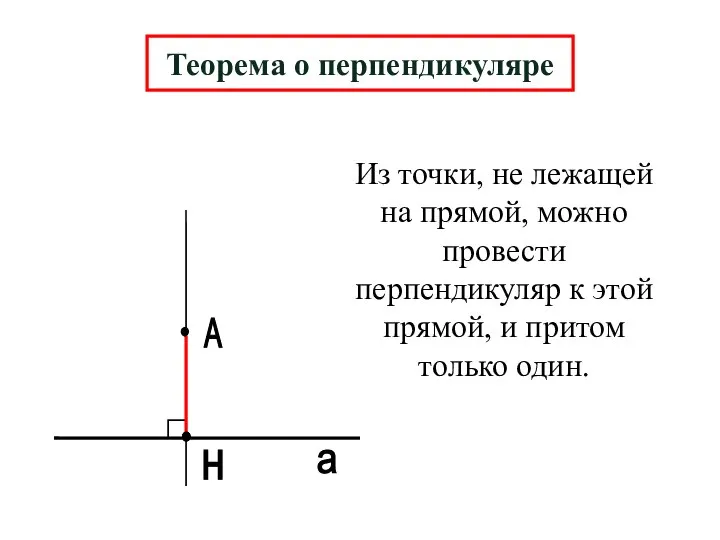
- 11. А н а Теорема о перпендикуляре Из точки, не лежащей на прямой, можно провести перпендикуляр к
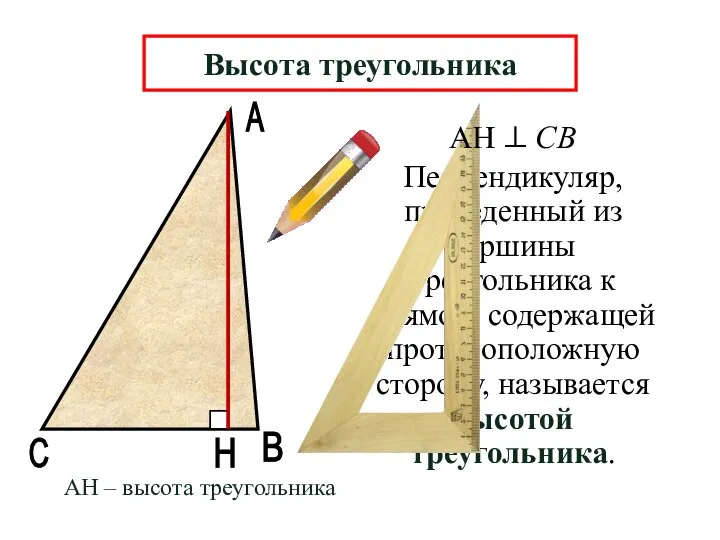
- 12. А В Н Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
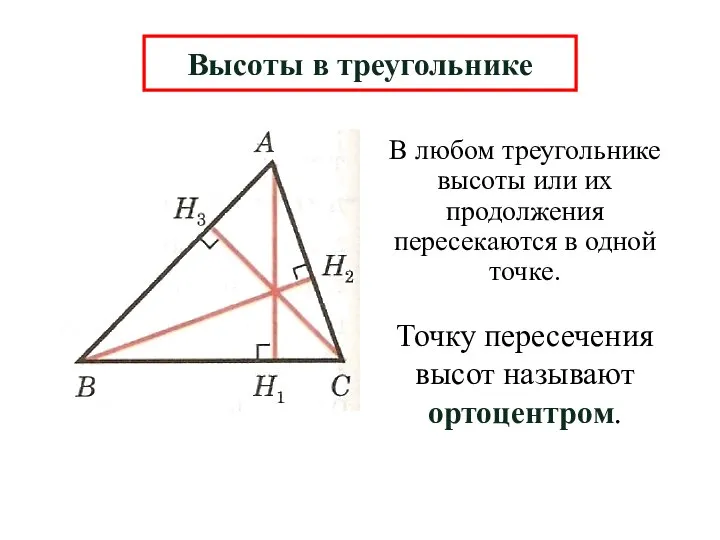
- 13. Высоты в треугольнике
- 14. В любом треугольнике высоты или их продолжения пересекаются в одной точке. Высоты в треугольнике Точку пересечения
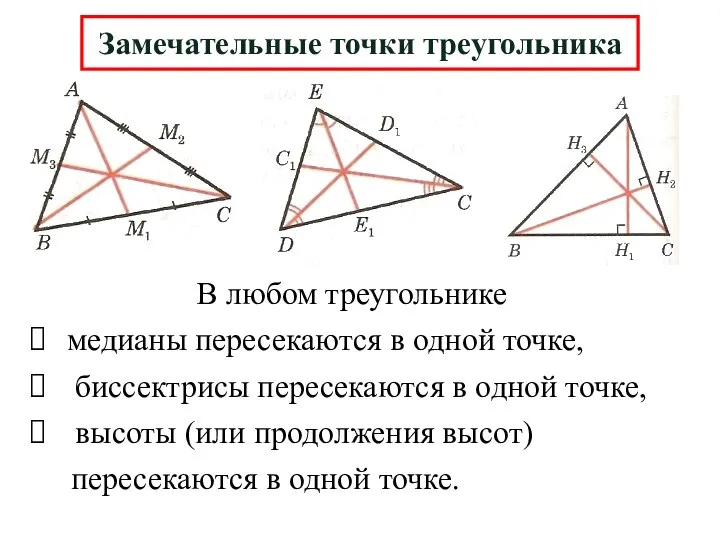
- 15. Замечательные точки треугольника В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке,
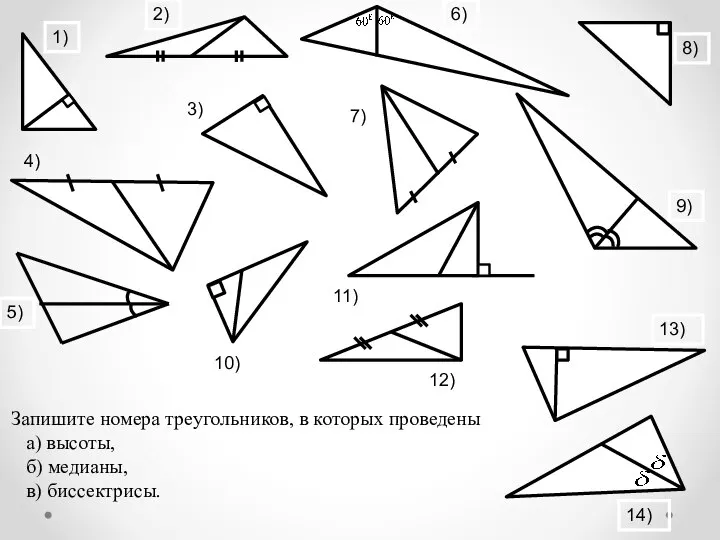
- 16. 2) 1) 5) 6) 7) 8) 9) 11) 12) 13) 14) 3) 4) 10) Запишите номера
- 17. ПРИЗНАКИ РАВЕНСТВА ФИГУР
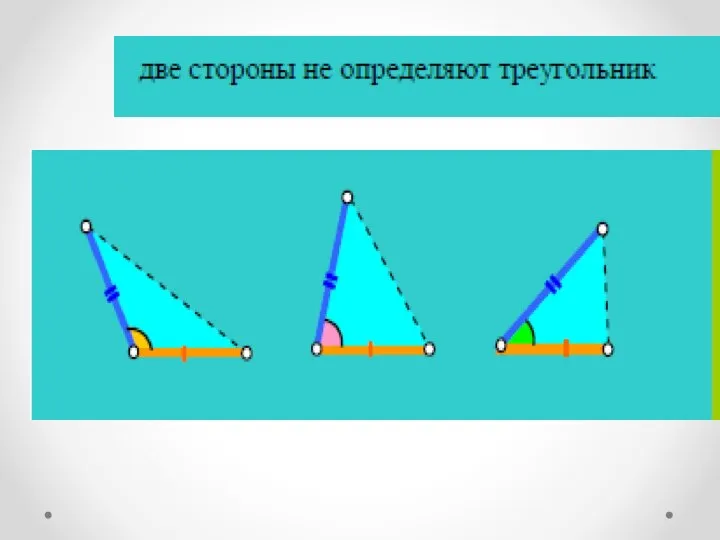
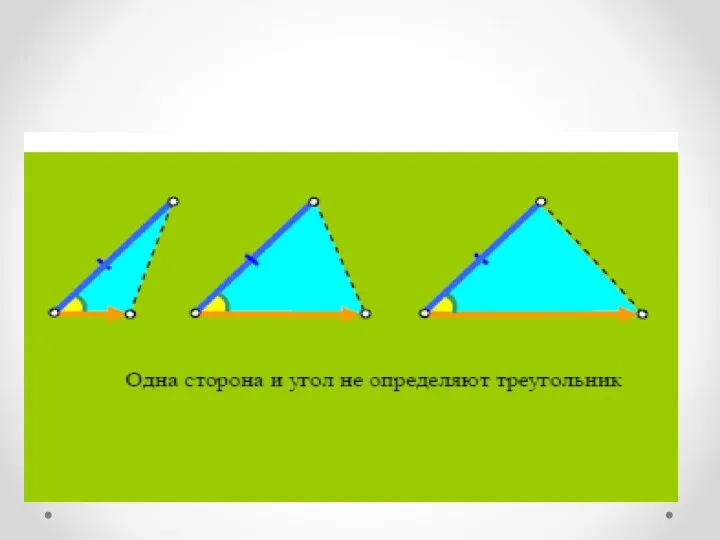
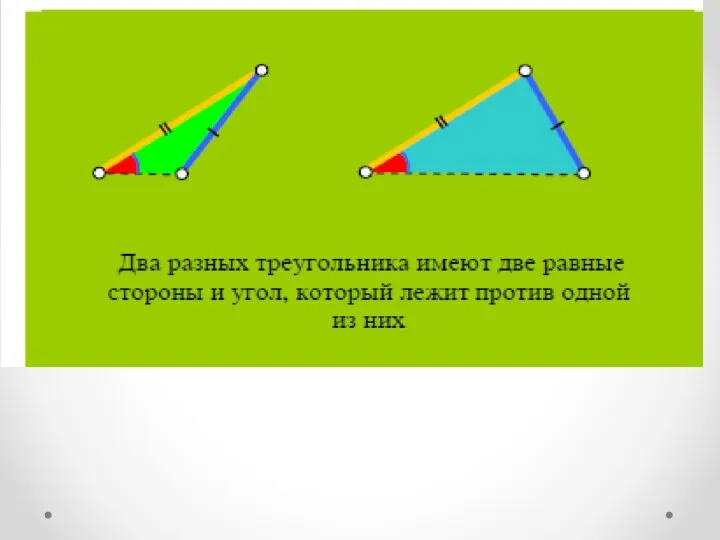
- 18. Что такое признаки равенства?
- 21. ПРИЗНАКИ
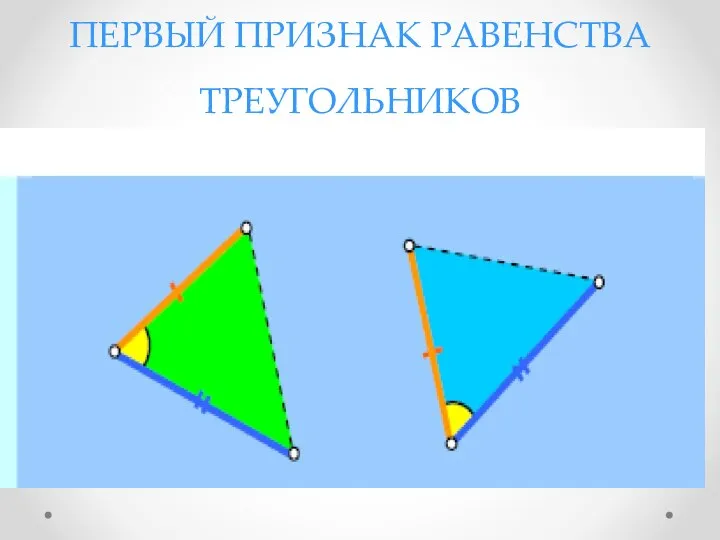
- 36. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
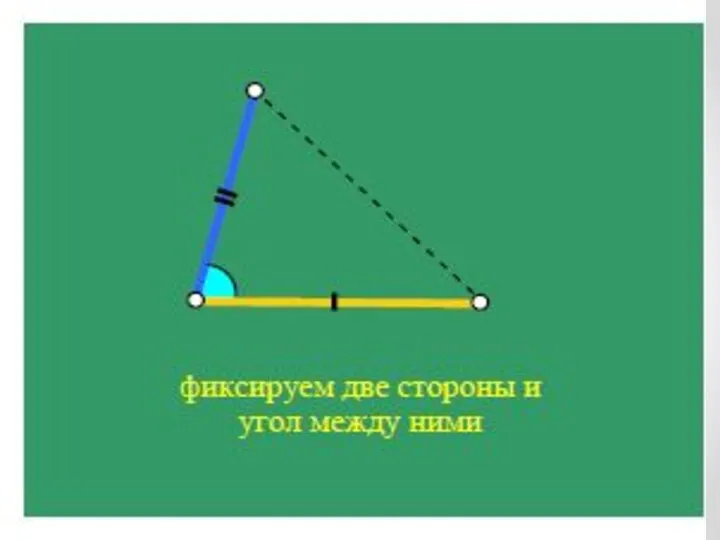
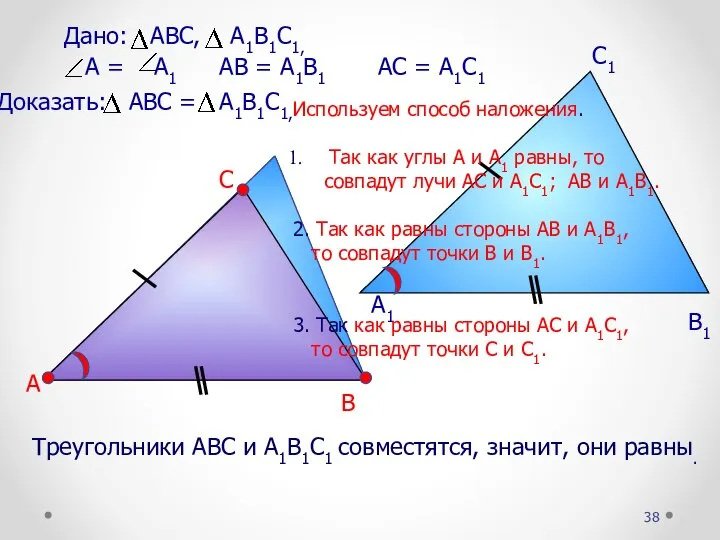
- 37. I признак равенства треугольников по двум сторонам и углу между ними. Если две стороны и угол
- 38. Треугольники АВС и А1В1С1 совместятся, значит, они равны. А В С А1 В1 С1 АВ =
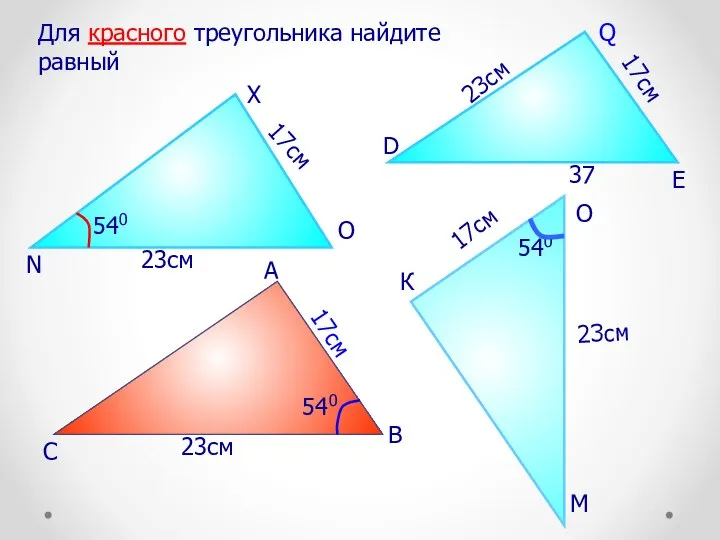
- 39. К 17см 23см Для красного треугольника найдите равный 23см 23см 23см 17см 17см 17см 37 540
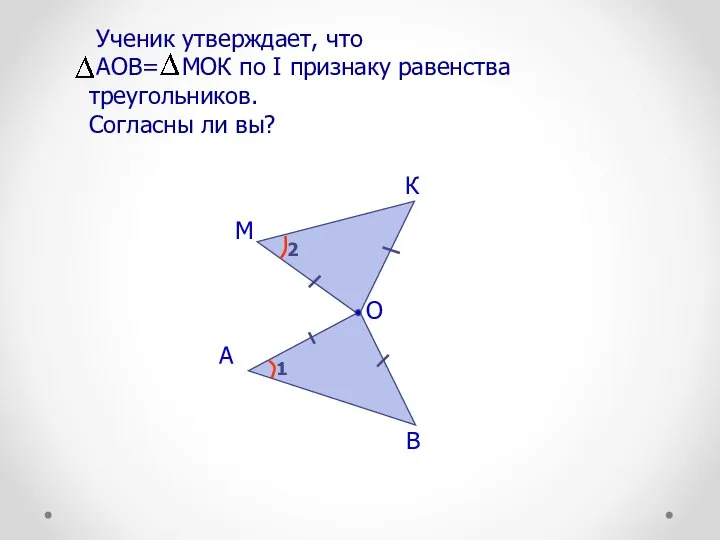
- 40. О А В К М Ученик утверждает, что АОВ= МОК по I признаку равенства треугольников. Согласны
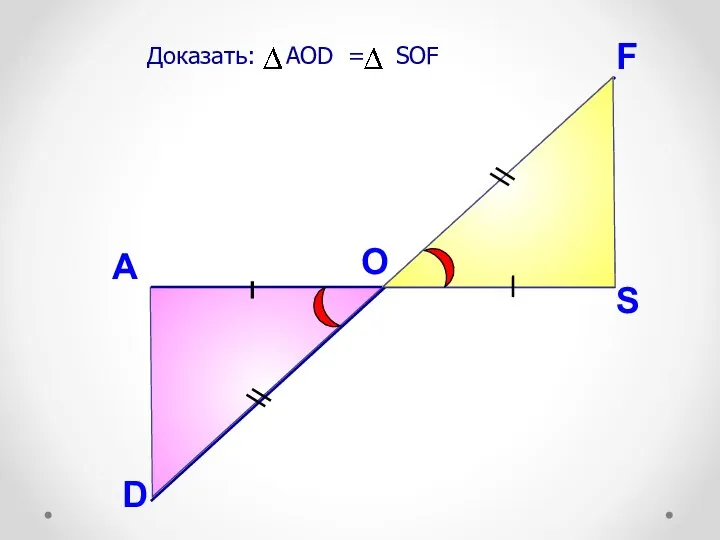
- 41. A Доказать: AOD = SOF O F S D
- 43. Скачать презентацию















 Uravnenia_i_neravenstva_Sistemy_uravneniy
Uravnenia_i_neravenstva_Sistemy_uravneniy Трапеция
Трапеция Турнир имени Лоповка
Турнир имени Лоповка Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  График квадратичной функции, содержащей переменную под знаком абсолютной величины
График квадратичной функции, содержащей переменную под знаком абсолютной величины Учебно-методический комплект по математике по ФГОС второй ступени
Учебно-методический комплект по математике по ФГОС второй ступени Введение в геометрию
Введение в геометрию Треугольник паскаля
Треугольник паскаля Пперпендикулярные прямые
Пперпендикулярные прямые Начертательная геометрия – это не просто, это очень просто
Начертательная геометрия – это не просто, это очень просто Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс
Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Тела и поверхности вращения
Тела и поверхности вращения Интерактивная игра-тренажёр. Сколько? Соотношение числа и цифры
Интерактивная игра-тренажёр. Сколько? Соотношение числа и цифры Вписанные и описанные четырехугольники
Вписанные и описанные четырехугольники Дифференциальные уравнения
Дифференциальные уравнения Понятие функции, предел
Понятие функции, предел Движения. 9-й класс
Движения. 9-й класс Окружность и круг. Задачи
Окружность и круг. Задачи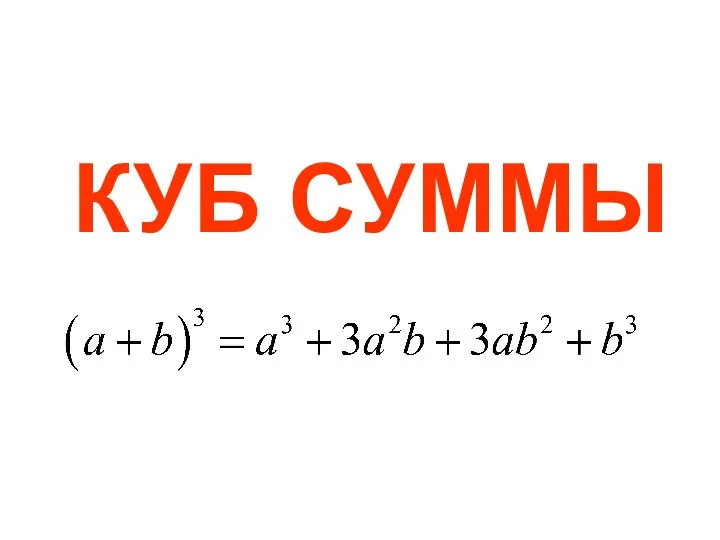 Куб суммы
Куб суммы Презентация на тему Комбинаторные задачи: размещения
Презентация на тему Комбинаторные задачи: размещения  Схемы к задачам
Схемы к задачам Функция у-сосх, её свойства и график
Функция у-сосх, её свойства и график Простейшие тригонометрические уравнения. Задания для устного счета
Простейшие тригонометрические уравнения. Задания для устного счета Отображения (функции)
Отображения (функции) Различные виды тестирования при изучении темы Десятичные дроби
Различные виды тестирования при изучении темы Десятичные дроби Логарифмы вокруг нас
Логарифмы вокруг нас Прикладная математика. Системы уравнений
Прикладная математика. Системы уравнений