Содержание
- 2. x²+2y=6 УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 2²+2∙1=6 ПАРА ЧИСЕЛ 2 И 1 – РЕШЕНИЕ УРАВНЕНИЯ
- 3. РЕШЕНИЕМ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ НАЗЫВАЕТСЯ ПАРА ЗНАЧЕНИЙ ПЕРЕМЕННЫХ, ОБРАЩАЮЩАЯ ЭТО УРАВНЕНИЕ В ВЕРНОЕ РАВЕНСТВО. (1;2),
- 4. 4²+2y=6 16+2y=6 2y=6-16 2y=-10 y=-5 (4;-5) 4²+2∙(-5)=6
- 5. x²+2y=6 2y=6-x² y=3-0,5∙x² УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ, ИМЕЮЩИЕ ОДНО И ТО ЖЕ МНОЖЕСТВО РЕШЕНИЙ, НАЗЫВАЮТСЯ РАВНОСИЛЬНЫМИ.
- 6. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение,
- 7. x²+2y=6 2y=6-x² y=3-0,5∙x² Если x=-2, то: y=3-0,5∙(-2)² y=3-0,5∙4 y=3-2 y=1
- 9. Скачать презентацию


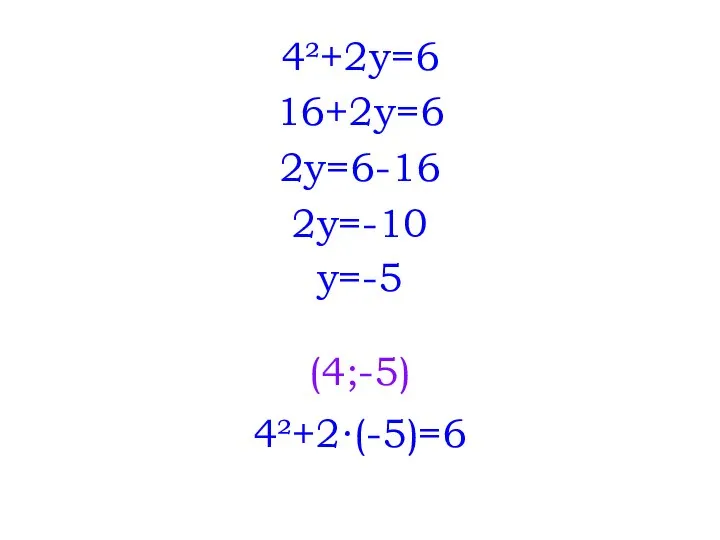


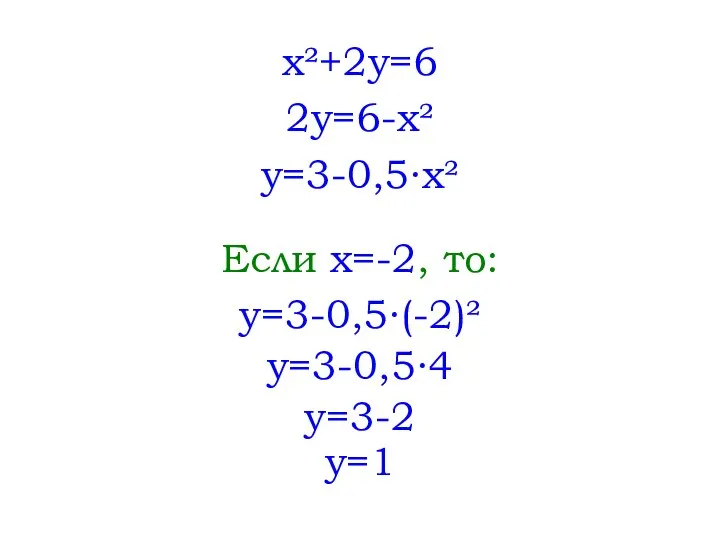
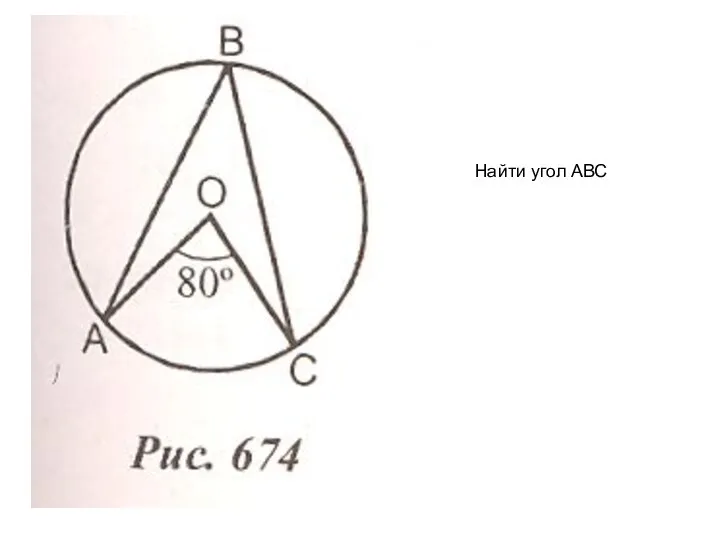 Найти угол АВС
Найти угол АВС Кто что любит поесть?
Кто что любит поесть? Математика в профессии сварщика
Математика в профессии сварщика Параллелограмм и его свойства и признаки
Параллелограмм и его свойства и признаки Метод интервалов. Задания для устного счета. Упражнение 3
Метод интервалов. Задания для устного счета. Упражнение 3 Презентация на тему Взаимно простые числа
Презентация на тему Взаимно простые числа  Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Математика. Задачи на кратное сравнение
Математика. Задачи на кратное сравнение Геометрия Евклида
Геометрия Евклида Умножение на двузначное число
Умножение на двузначное число Форматы вывода результата вычислений и логические операции в MATLAB
Форматы вывода результата вычислений и логические операции в MATLAB Вариационные ряды и их характеристики. Глава 3. Элементы математической статистики
Вариационные ряды и их характеристики. Глава 3. Элементы математической статистики Дифференциальные уравнения
Дифференциальные уравнения Линейная функция. Построение графика функции у= 2х-1
Линейная функция. Построение графика функции у= 2х-1 Сложение и вычитание рациональных чисел
Сложение и вычитание рациональных чисел Матрицы и определители
Матрицы и определители 1_urok_ponyatie_vektora
1_urok_ponyatie_vektora Таблица сложения в пределах 20. 1 класс
Таблица сложения в пределах 20. 1 класс Площадь треугольника
Площадь треугольника Функция y = cos x. Ее свойства и график
Функция y = cos x. Ее свойства и график Параллельные прямые в пространстве
Параллельные прямые в пространстве Выполните деление
Выполните деление Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Презентация на тему Векторы в пространстве Геометрия
Презентация на тему Векторы в пространстве Геометрия  Группировка слагаемых. Скобки
Группировка слагаемых. Скобки Теорія ймовірностей, ймовірнісні процеси і математична статистика
Теорія ймовірностей, ймовірнісні процеси і математична статистика Объединение множеств
Объединение множеств Повторение: Числа
Повторение: Числа