Статистический анализ данных в пакете Statistica

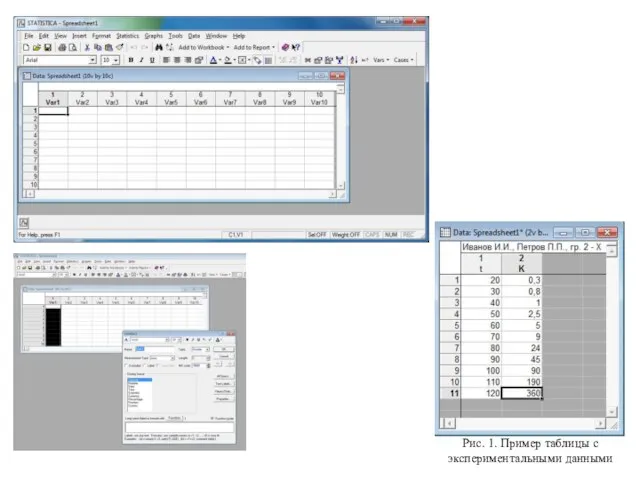
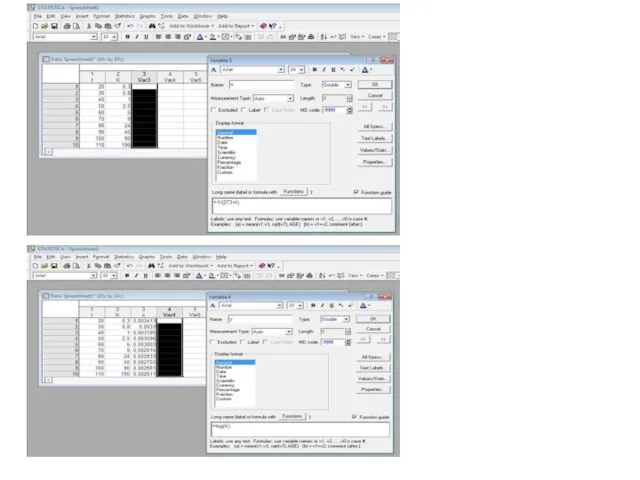
Рис. 1. Пример таблицы с экспериментальными данными

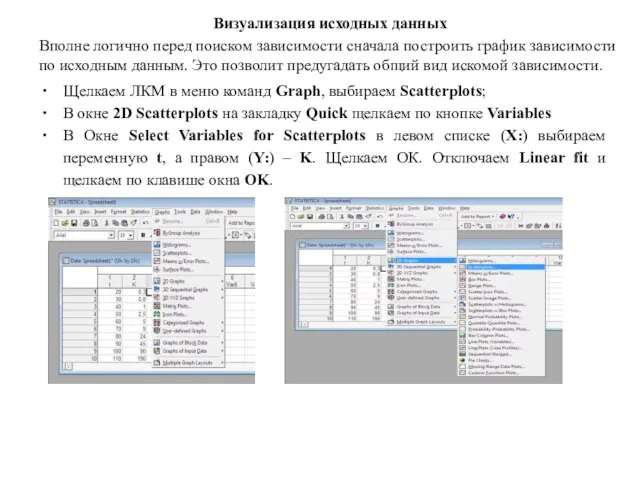
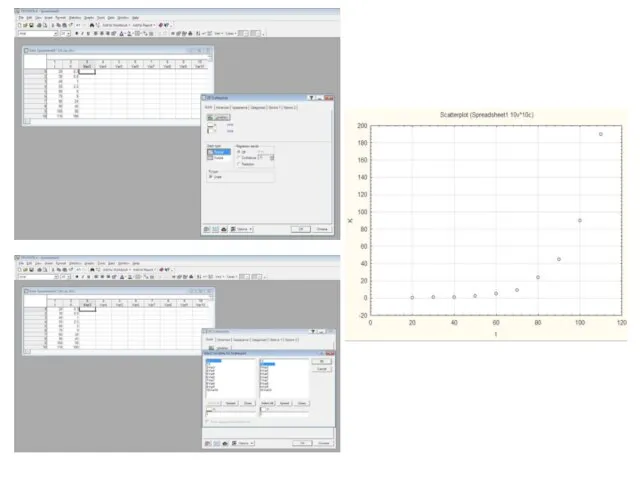
Щелкаем ЛКМ в меню команд Graph, выбираем Scatterplots;
В окне 2D Scatterplots на закладку Quick щелкаем по кнопке Variables
В Окне Select Variables for Scatterplots в левом списке (X:) выбираем переменную t, а правом (Y:) – K. Щелкаем ОК. Отключаем Linear fit и щелкаем по клавише окна OK.
Визуализация исходных данных
Вполне логично перед поиском зависимости сначала построить график зависимости по исходным данным. Это позволит предугадать общий вид искомой зависимости.

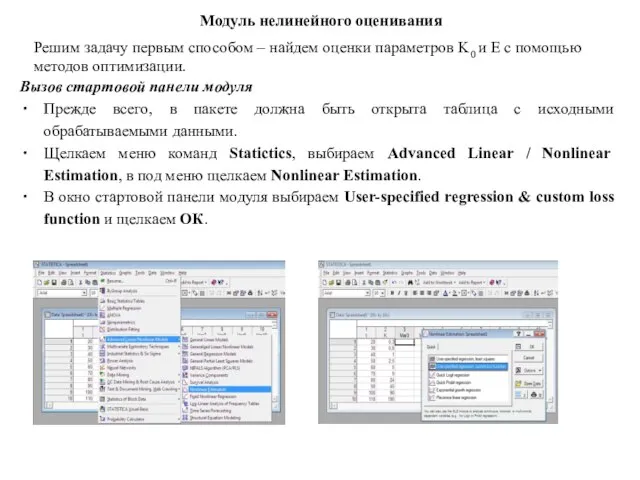
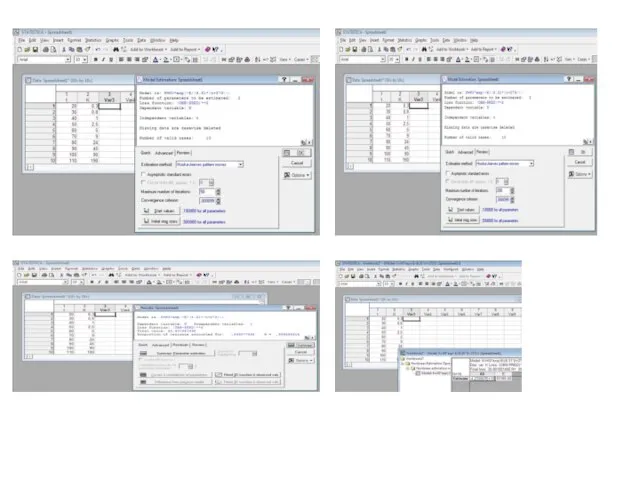
Модуль нелинейного оценивания
Решим задачу первым способом – найдем оценки параметров K0 и E с помощью методов оптимизации.
Вызов стартовой панели модуля
Прежде всего, в пакете должна быть открыта таблица с исходными обрабатываемыми данными.
Щелкаем меню команд Statictics, выбираем Advanced Linear / Nonlinear Estimation, в под меню щелкаем Nonlinear Estimation.
В окно стартовой панели модуля выбираем User-specified regression & custom loss function и щелкаем ОК.

Выбор минимизируемой функции и численного метода поиска оценок:
В окне User-specified regression щелкаем OK. Появляется окно Model Estimation: в информационной части приводятся искомая функция (Model), число оцениваемых параметров (Number of parameter to be estimate), зависимая (Depended) и независимая (Independent) переменная, число опытов (Number of Valid Cases).
Ниже выбираем вкладку Advanced, в поле Estimation Method выбираем численный метод Хука-Дживса (Hoove-Jeevs pattern moves). Число итераций Maxium Number of iterations и точность метода Convergence не меняем. В данном окне можно также задать начальные значения (кнопка Start Values) и начальный шаг поиска (кнопка Initial Step Values) для оцениваемых параметров в виде чисел с плавающей запятой (мантисс, к примеру, 5.2E9, что означает 5.2*109). Однако в данной задаче в силу простоты искомой функции мы их не задаем. Щелкаем OK в окне Model Estimation.

Нахождение оценок с помощью линейного регрессионного анализа

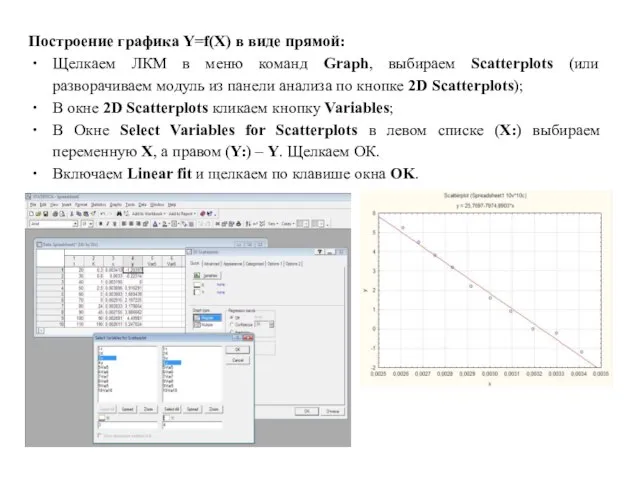
Построение графика Y=f(X) в виде прямой:
Щелкаем ЛКМ в меню команд Graph, выбираем Scatterplots (или разворачиваем модуль из панели анализа по кнопке 2D Scatterplots);
В окне 2D Scatterplots кликаем кнопку Variables;
В Окне Select Variables for Scatterplots в левом списке (X:) выбираем переменную X, а правом (Y:) – Y. Щелкаем ОК.
Включаем Linear fit и щелкаем по клавише окна OK.

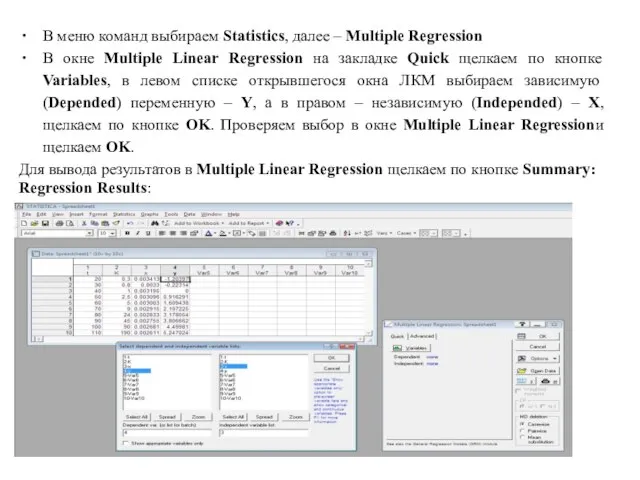
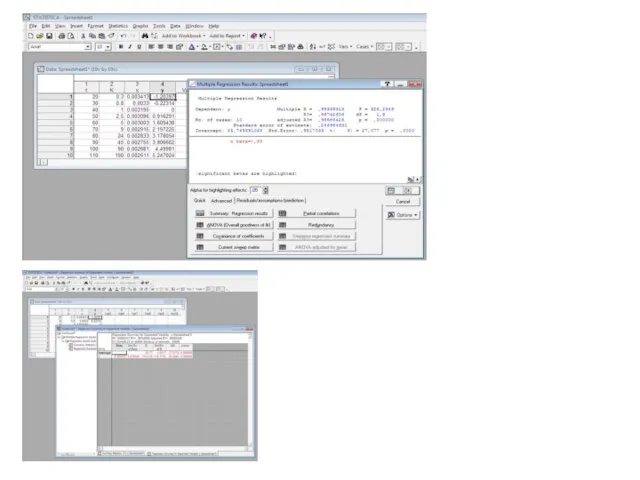
В меню команд выбираем Statistics, далее – Multiple Regression
В окне Multiple Linear Regression на закладке Quick щелкаем по кнопке Variables, в левом списке открывшегося окна ЛКМ выбираем зависимую (Depended) переменную – Y, а в правом – независимую (Independed) – X, щелкаем по кнопке OK. Проверяем выбор в окне Multiple Linear Regressionи щелкаем OK.
Для вывода результатов в Multiple Linear Regression щелкаем по кнопке Summary: Regression Results: