- Главная
- Математика
- Элементы теории множеств. Множества и основные операции над ними

Содержание
- 2. ОПР.1: под множеством М понимается совокупность некоторых объектов, которые будут называться элементами множества М.Элементы множества различны.
- 3. II Множество можно задать перечислением принадлежащих ему элементов или указанием свойств, которым элементы множества должны удовлетворять:
- 14. Скачать презентацию
Слайд 2ОПР.1: под множеством М понимается совокупность некоторых объектов, которые будут называться элементами
ОПР.1: под множеством М понимается совокупность некоторых объектов, которые будут называться элементами

множества М.Элементы множества различны.
ПР: Множество S страниц в книге; множество N натуральных чисел 1,2,3,….;
множество студентов в группе; множество отличников колледжа.
ПР: Множество S страниц в книге; множество N натуральных чисел 1,2,3,….;
множество студентов в группе; множество отличников колледжа.
ОПР.2: если объект x является элементом множества М, то говорят, что
х принадлежит М.Обозначение: x М. В противном случае говорят, что x не принадлежит М. Обозначение : x М.Элементы множества сами могут является множествами.
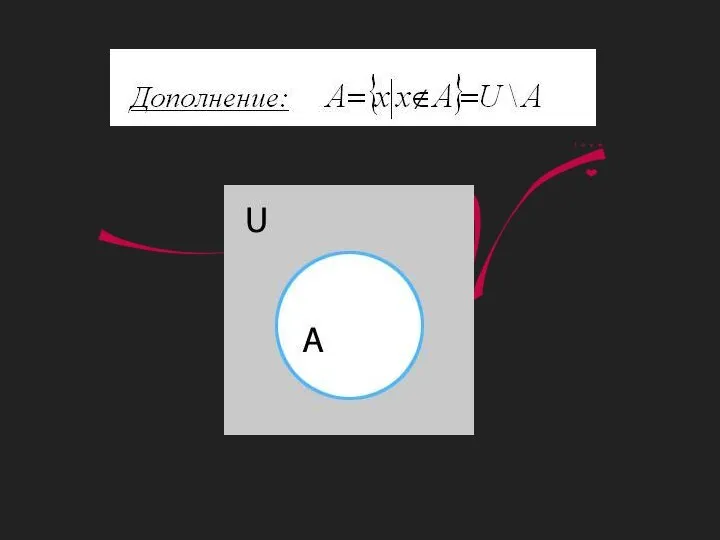
ОПР.3: множество, не содержащее элементов, называется пустым - .
Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсумом).
I
Слайд 3II
Множество можно задать перечислением принадлежащих ему элементов или указанием свойств, которым элементы
II
Множество можно задать перечислением принадлежащих ему элементов или указанием свойств, которым элементы

множества должны удовлетворять:
перечислением:
перечислением:
указанием свойств:

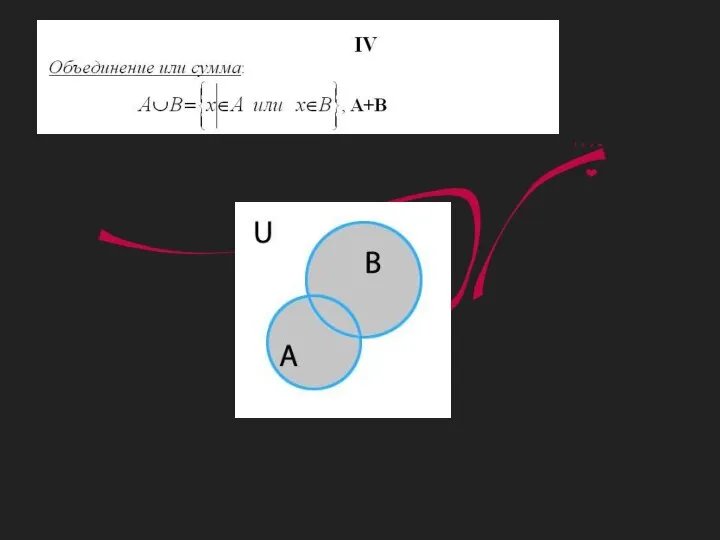
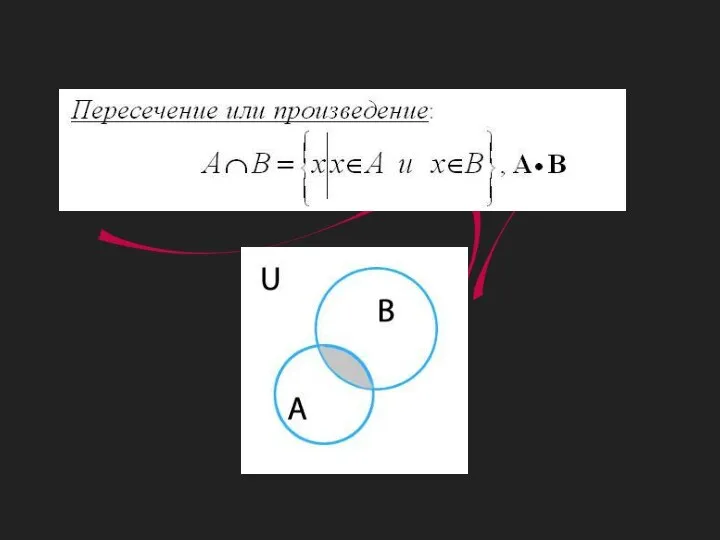
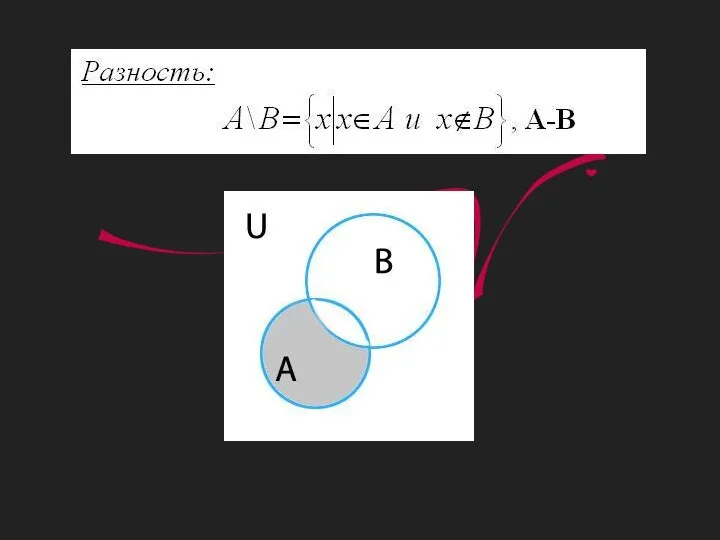
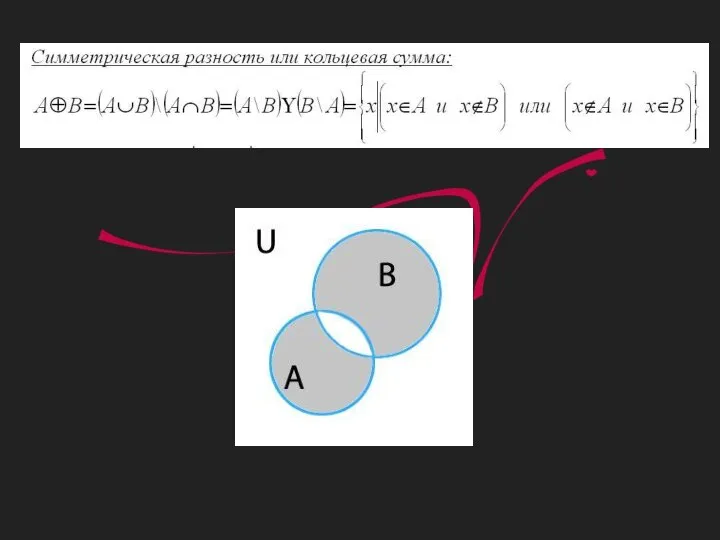



 Системы и совокупности неравенств с одной переменной
Системы и совокупности неравенств с одной переменной Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии Графики кусочных функций
Графики кусочных функций Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Решение задач с помощью составления систем уравнений. 9 класс
Решение задач с помощью составления систем уравнений. 9 класс Порядковый счёт в пределах 10
Порядковый счёт в пределах 10 Нестандартные уравнения
Нестандартные уравнения Презентация на тему Космическое путешествие 1 класс
Презентация на тему Космическое путешествие 1 класс  Методы многокритериальной оптимизации
Методы многокритериальной оптимизации Десятичные дроби
Десятичные дроби Умножение десятичных дробей. Космическое путешествие
Умножение десятичных дробей. Космическое путешествие Наибольшее и наименьшее значение функций
Наибольшее и наименьшее значение функций Квадратные уравнения
Квадратные уравнения Презентация на тему Свойства сложения и умножения
Презентация на тему Свойства сложения и умножения  Разложим по полочкам задачи на смеси. Интегрированный урок по математике и химии
Разложим по полочкам задачи на смеси. Интегрированный урок по математике и химии Правильные многогранники и ИДСЗ
Правильные многогранники и ИДСЗ Порядок выполнения действий. Скобки
Порядок выполнения действий. Скобки Математичний диктант. Паралелограм
Математичний диктант. Паралелограм Презентация на тему Решение нестандартных задач
Презентация на тему Решение нестандартных задач 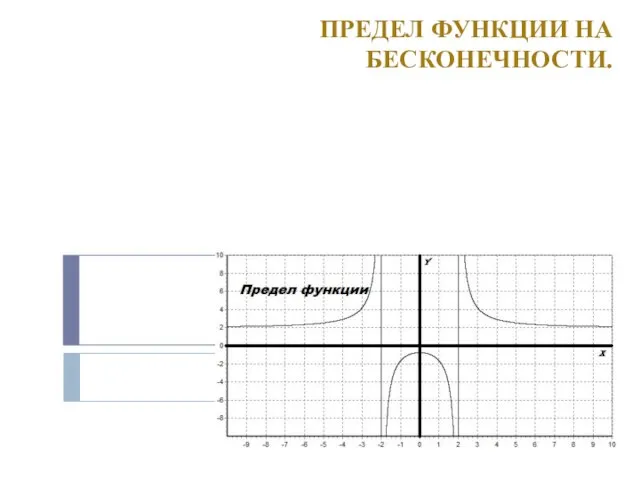 Predel_funktsii
Predel_funktsii Теорема Пифагора
Теорема Пифагора Формула Бернулли
Формула Бернулли Решение задач с помощью уравнений
Решение задач с помощью уравнений Признаки параллельности прямых
Признаки параллельности прямых Презентация на тему Линейная функция и её график
Презентация на тему Линейная функция и её график  Длина окружности. Площадь
Длина окружности. Площадь Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными Скалярное произведение векторов
Скалярное произведение векторов