Слайд 2Типичные проявления нарушения полноценности аргументации
незаконные обобщения;
Перебор частных случаев ≠ решение

Слайд 3Типичные проявления нарушения полноценности аргументации
незаконные обобщения;
Перебор частных случаев ≠ решение
1.а) Разбейте

квадрат на два равных пятиугольника.
б) Как разбить квадрат на два равных 11-угольника?
в) Как разбить квадрат на два равных n-угольника, если n − нечётное число?
2. Докажите, что клетчатый квадрат с вырезанной левой верхней клеткой можно разбить на клетчатые уголки из трёх клеток. Для квадрата со стороной
а) 4 клетки
б) 8 клеток
в) 1024 клетки
Слайд 4Типичные проявления нарушения полноценности аргументации
2) необоснованные аналогии;
По аналогии…
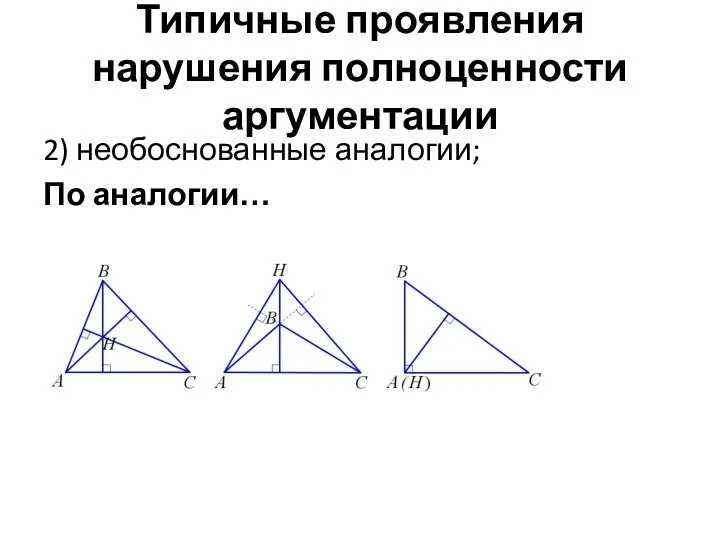
Слайд 5Типичные проявления нарушения полноценности аргументации
3) неполнота дизъюнкций;
Рассмотрены не все возможные ситуации в

задаче
Слайд 7Типичные проявления нарушения полноценности аргументации
4) неполнота (невыдержанность) классификации.
Потерян класс некоторого понятия
а) простые

и составные (единица)
б) остроугольные и тупоугольные (прямоугольные)
в) положительные и отрицательные (нуль)
Слайд 8Ошибки: Неумение работать с условием

Слайд 9Ошибки: ох уж эти числа
Нуль – никакое (и снова неполнота классификации)
Тип числа
Различные/равные

Слайд 10Ошибки: Оценка + пример
Какое наибольшее/
наименьшее…?
- Пример
Оценка
Задача. Какое минимальное число шашек

надо взять, чтобы при любой их расстановке на клетках шахматной доски (8×8) обязательно встретились 4 шашки, стоящие друг за другом по горизонтали?
Слайд 11Ошибки: Доказательство неравенств

Слайд 12Ошибки: Доказательство неравенств

Слайд 13Ошибки: Доказательство неравенств

Слайд 14Ошибки по незнанию:
Вписанные углы
1. Угол:
центральный,
вписанный,
с вершиной внутри круга,
с вершиной

вне круга,
между хордой и касательной.
2. Свойства вписанного в окружность четырёхугольника
3. Признаки вписанного в окружность четырёхугольника
Слайд 15Общие подходы, методы, приемы
1. Метод перебора (не подбор);
2. Прямое или конструктивное доказательство

(«Существует(ют) ли…?», «Можно ли?»);
3. Способ доказательства «от противного»;
4. Косвенные доказательства (принцип Дирихле);
5. Метод «крайнего»;
6. Рассуждения по индукции (ММИ).














 Комбинаторная задача с монетами
Комбинаторная задача с монетами Тестовые задания
Тестовые задания Производная и ее применение
Производная и ее применение Окружность и круг
Окружность и круг Математическая статистика
Математическая статистика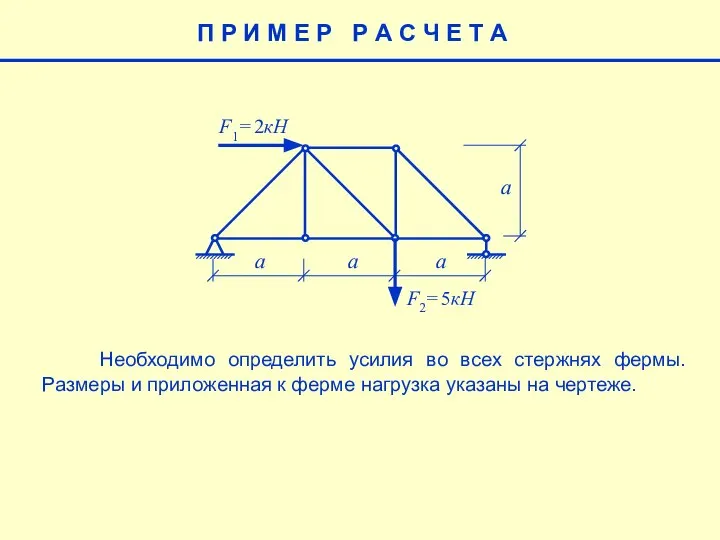 Методы расчета ферм
Методы расчета ферм Презентация на тему Золотое сечение-гармония математики
Презентация на тему Золотое сечение-гармония математики  Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Тела вращения. Урок 142
Тела вращения. Урок 142 Элементы теории вероятностей
Элементы теории вероятностей математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Деление дробей. Решение задач
Деление дробей. Решение задач Линейные алгоритмы
Линейные алгоритмы Круговая окружность
Круговая окружность Эйлеровы и гамильтоновы графы
Эйлеровы и гамильтоновы графы Возрастание и убывание функции
Возрастание и убывание функции Таблица Шульте
Таблица Шульте Планиметрия малыми порциями
Планиметрия малыми порциями Вычитание (Помоги Буратино исправить ошибки)
Вычитание (Помоги Буратино исправить ошибки)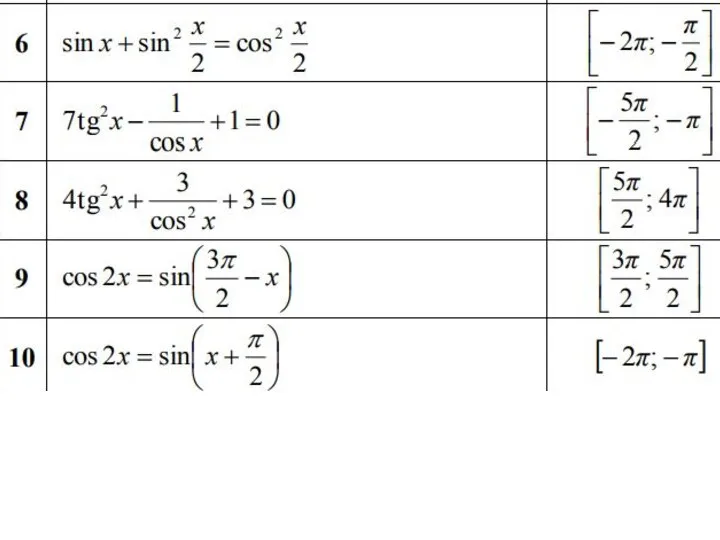 Решение уравнений
Решение уравнений 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Методы статистического анализа литературных текстов
Методы статистического анализа литературных текстов Прямоугольные треугольники
Прямоугольные треугольники Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08 Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР)
Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР) Натуральный ряд чисел
Натуральный ряд чисел Многогранный угол. Трёхгранный угол
Многогранный угол. Трёхгранный угол