Слайд 154. Множество всех функций у = f (x), определенных и непрерывных на

отрезке [a, b], для которых обычными правилами математического анализа определены операции сложения таких функций и умножения их на число, является линейным пространством. Пусть f (x) и g (x) ⎯ функции, определенные и непрерывные на отрезке [a, b], тогда их сумма f (x) + g (x) = h (x) ⎯ определенная и непрерывная во всех точках отрезка [a, b] функция. Аналогично, при умножении функции на любое число получаем функцию, определенную и непрерывную на отрезке [a, b], т. е. принадлежащую рассматриваемому множеству. В качестве нулевого элемента в этом множестве берем функцию, имеющую значение нуль во всех точках отрезка [a, b], т. е. функцию у = 0 ⎯ часть оси Ох, а именно отрезок а ≤ х ≤ b. Противоположным элементом для функции f (x), будет функция −f (x). Остальные аксиомы будут выполняться в силу того, что все операции над функциями сводятся в каждой конкретной точке отрезка к операциям над числами, для которых эти аксиомы верны. Следовательно, совокупность функций, непрерывных на отрезке [a, b], с обычными операциями сложения функций и умножения функции на число является линейным пространством, которое называют пространством непрерывных функций на отрезке [a, b] и обозначают С[а, b].



















 Золотое сечение в Web-дизайне
Золотое сечение в Web-дизайне Презентация на тему Число 0 Цифра 0
Презентация на тему Число 0 Цифра 0 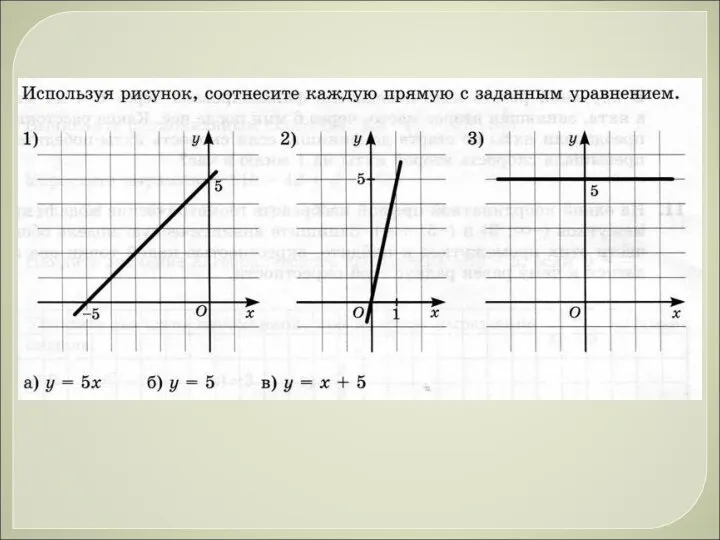 Соотношение прямой с заданным уравнением
Соотношение прямой с заданным уравнением Великие матекматики и их открытия
Великие матекматики и их открытия Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Куб. Измерения куба
Куб. Измерения куба Временные ряды
Временные ряды Многогранники
Многогранники Кластерный анализ. Лекция 8
Кластерный анализ. Лекция 8 Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Смежные и вертикальные углы
Смежные и вертикальные углы Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9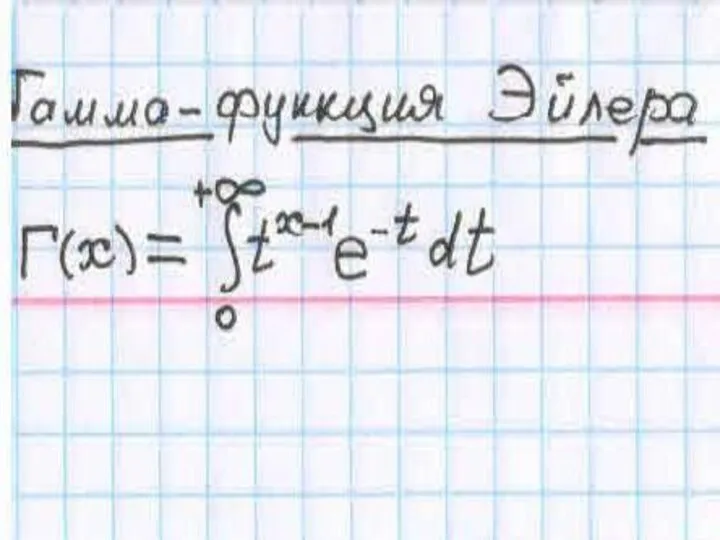 Гамма-функция Эйлера
Гамма-функция Эйлера Проценты (5)
Проценты (5) Восход и заход солнца с точки зрения графика тригонометрических функций
Восход и заход солнца с точки зрения графика тригонометрических функций Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат
Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат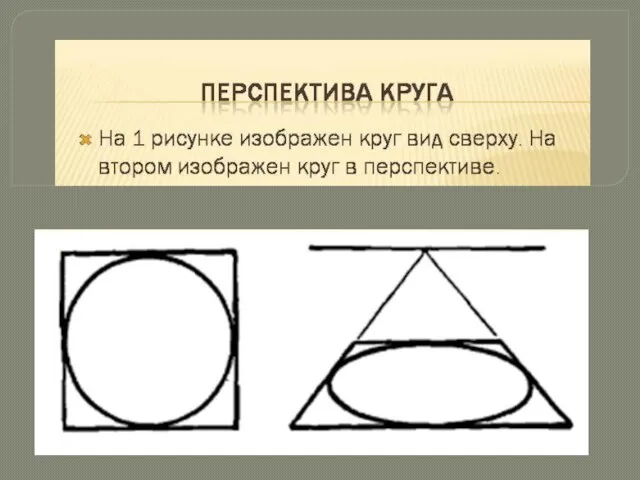 Перспектива круга
Перспектива круга Математика. Русский язык. Технология. Вопросы
Математика. Русский язык. Технология. Вопросы Частные производные. Лекция 17
Частные производные. Лекция 17 797821
797821 Число и цифра 5
Число и цифра 5 Понятие угла. Тригонометрические формулы
Понятие угла. Тригонометрические формулы Օբյեկտ-կողմնորոշված ծրագրավորման լեզու
Օբյեկտ-կողմնորոշված ծրագրավորման լեզու Компоненты вычитания
Компоненты вычитания теория вероятностей задачи
теория вероятностей задачи Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг)
Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг) Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)
Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)