Содержание
- 2. План занятия 1. Эйлеров цикл и эйлеров граф: определения 2. Гамильтоновы графы 3. Алгоритмы поиска эйлеровых
- 3. ПОВТОРЕНИЕ: МАРШРУТЫ, ЦЕПИ, ЦИКЛЫ Маршрутом в графе называется последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной
- 4. Длиной маршрута называют число ребер в нем, причем каждое ребро считается столько раз, сколько раз оно
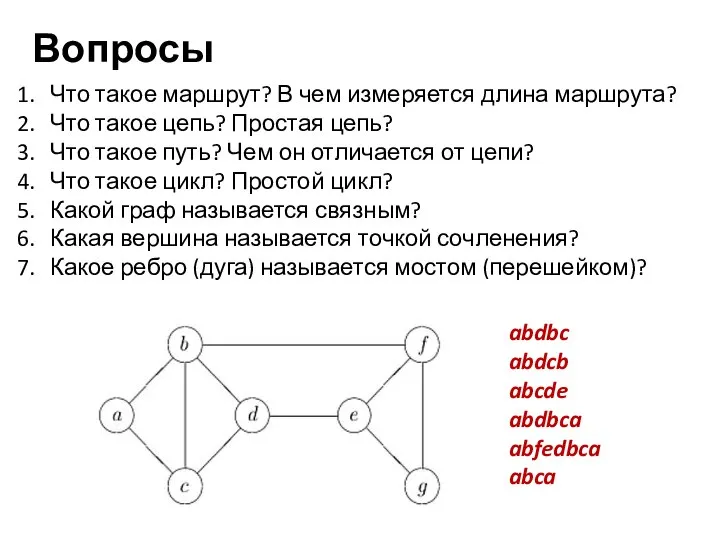
- 5. Что такое маршрут? В чем измеряется длина маршрута? Что такое цепь? Простая цепь? Что такое путь?
- 6. ОПРЕДЕЛЕНИЯ Эйлеровым путем графа называется путь, содержащий все ребра графа ровно один раз Эйлеровым циклом называется
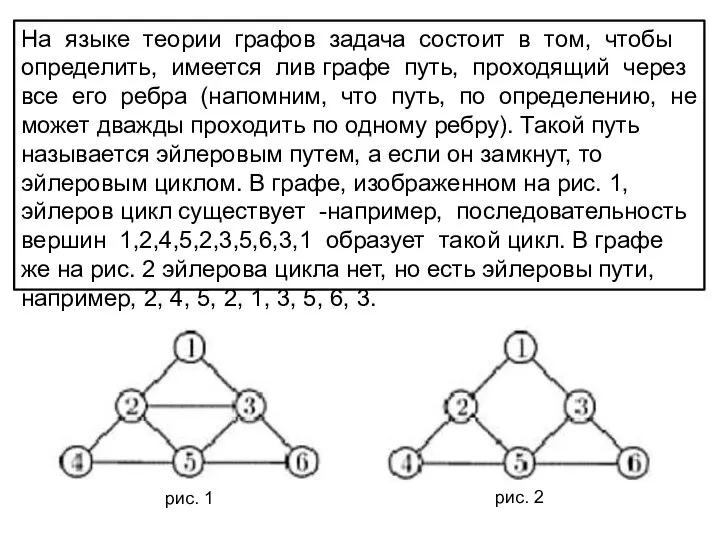
- 7. На языке теории графов задача состоит в том, чтобы определить, имеется лив графе путь, проходящий через
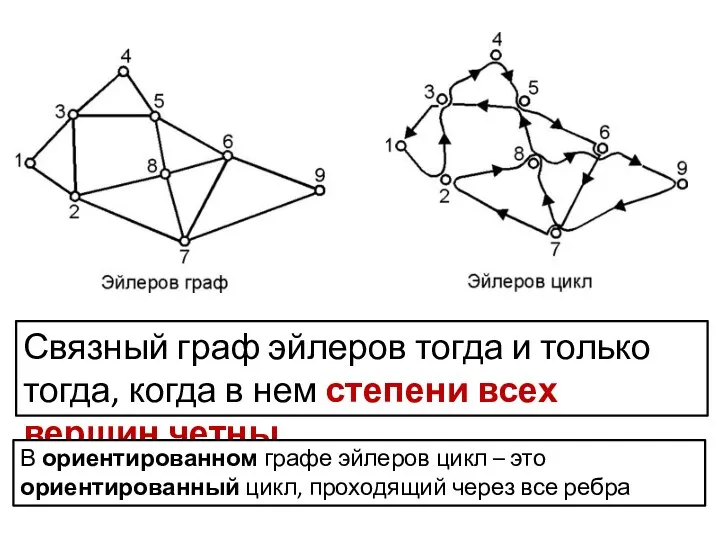
- 8. Связный граф эйлеров тогда и только тогда, когда в нем степени всех вершин четны В ориентированном
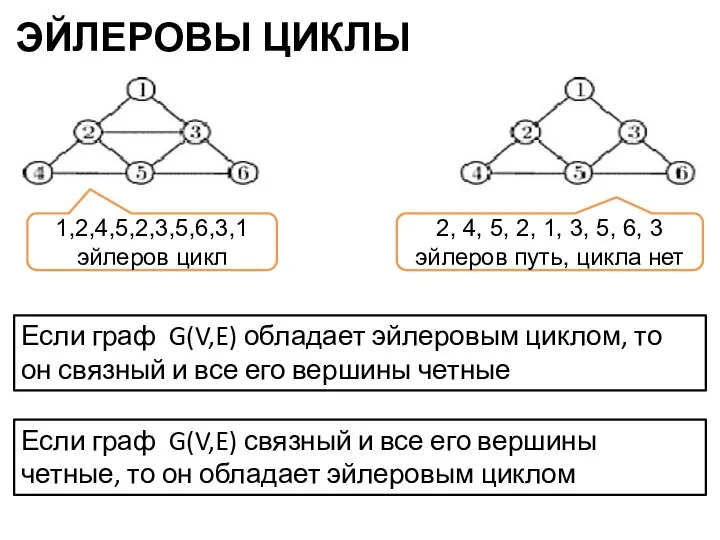
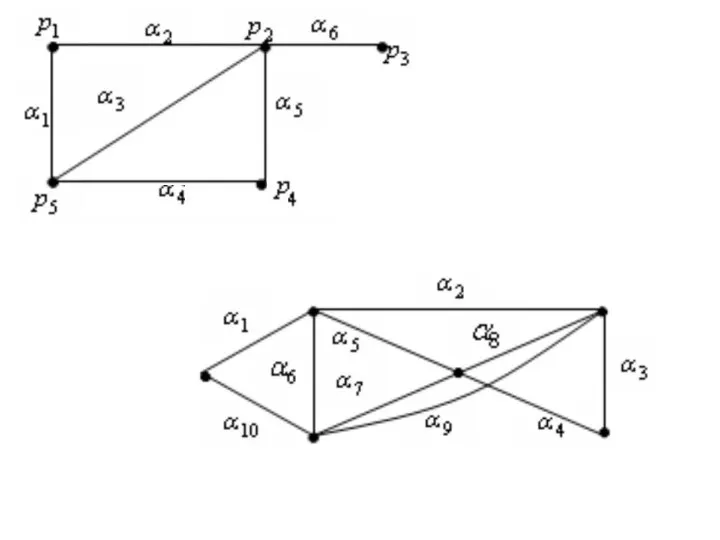
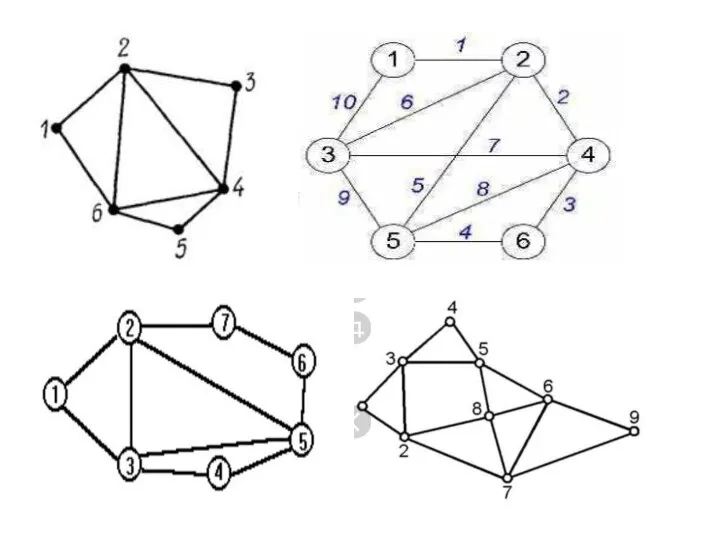
- 9. ЭЙЛЕРОВЫ ЦИКЛЫ 1,2,4,5,2,3,5,6,3,1 эйлеров цикл 2, 4, 5, 2, 1, 3, 5, 6, 3 эйлеров путь,
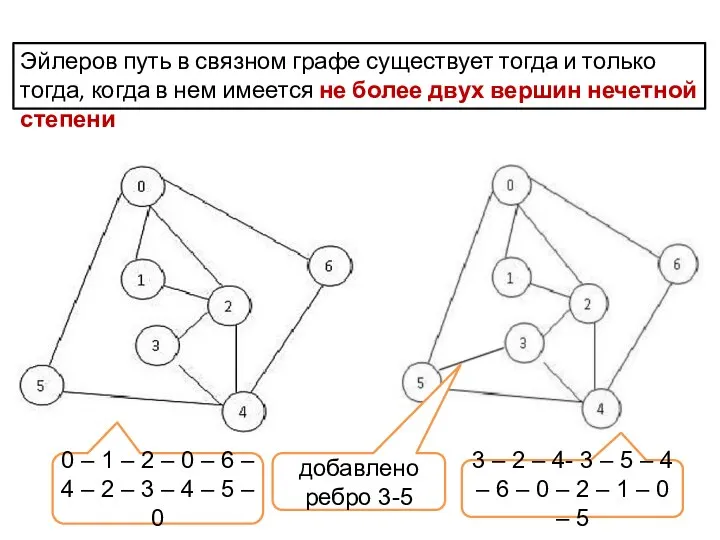
- 10. Эйлеров путь в связном графе существует тогда и только тогда, когда в нем имеется не более
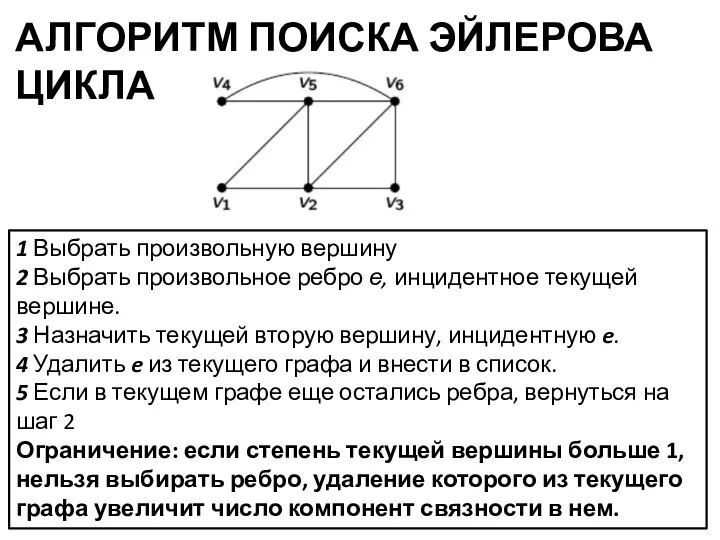
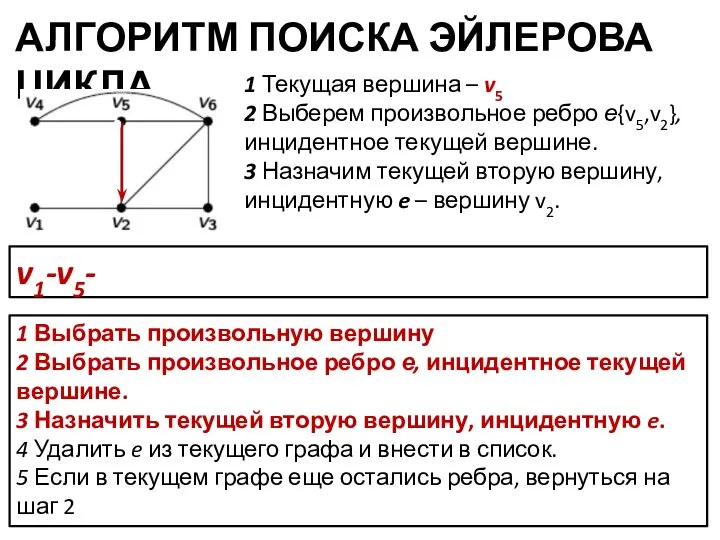
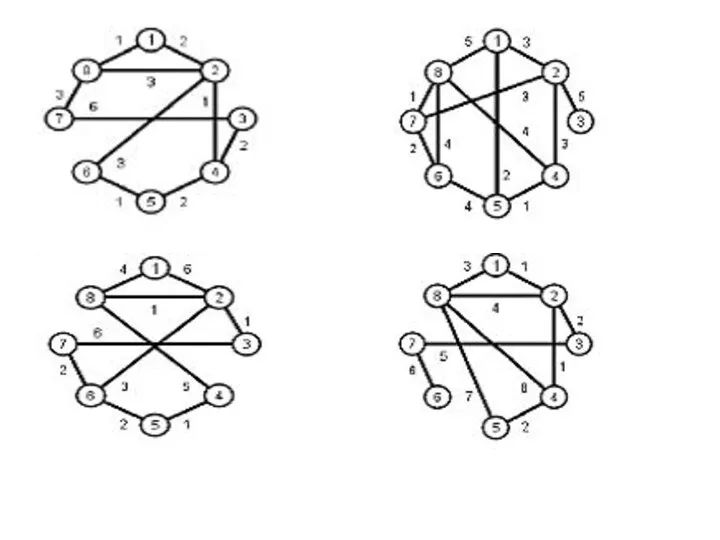
- 11. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
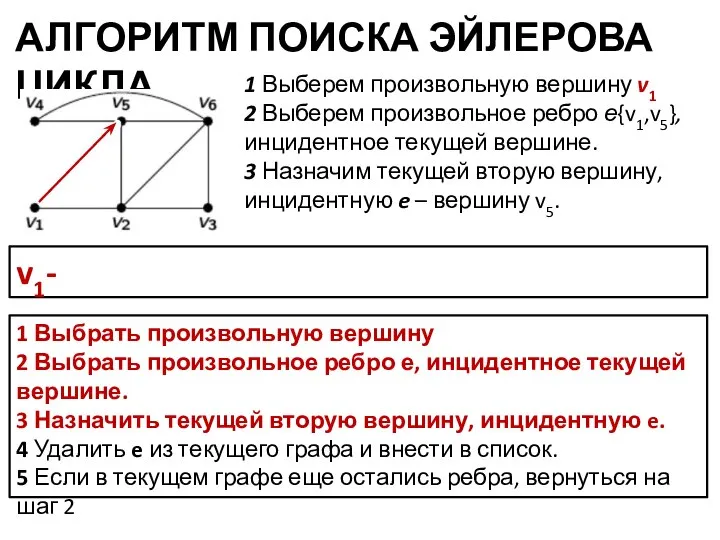
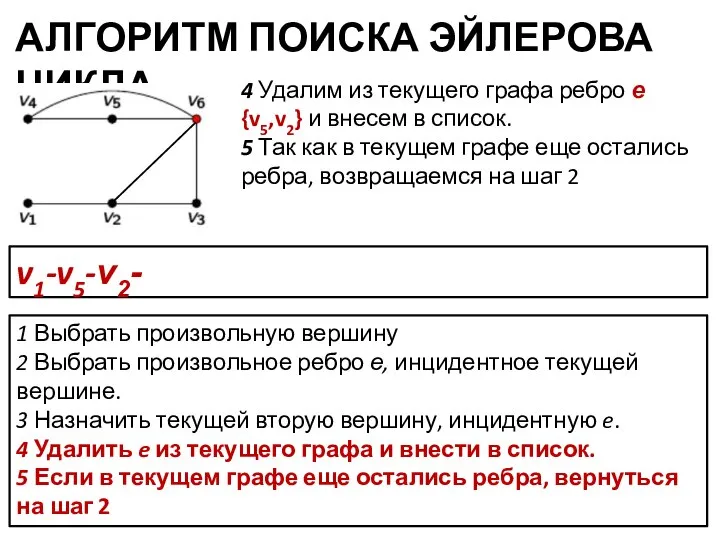
- 12. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
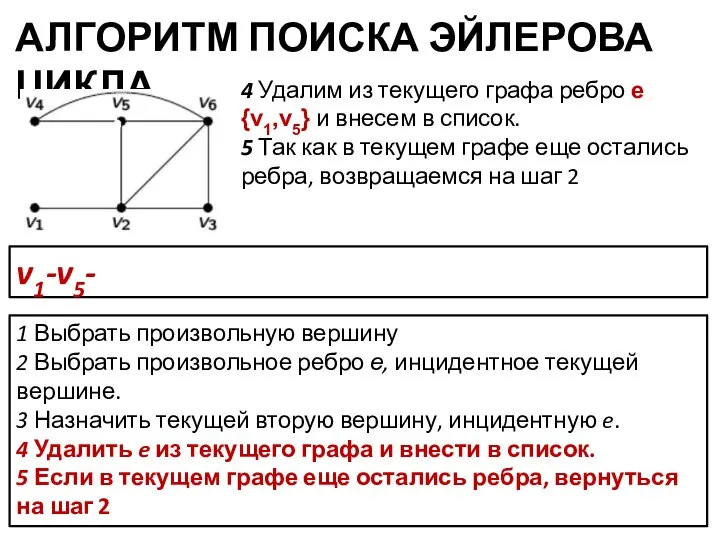
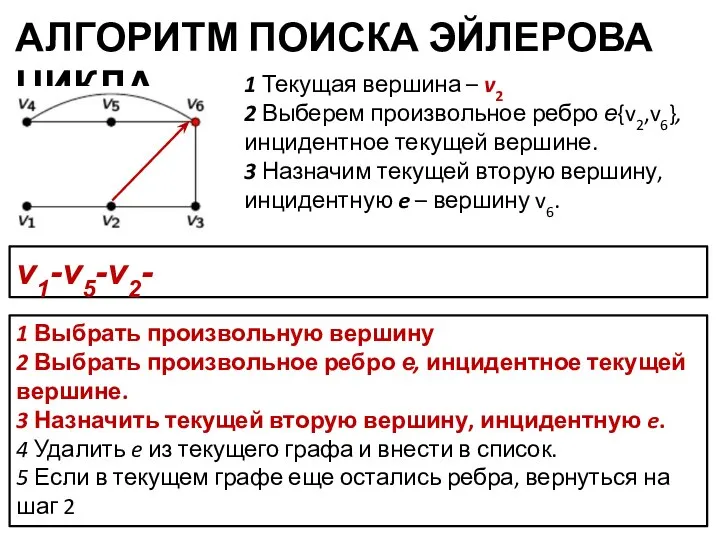
- 13. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
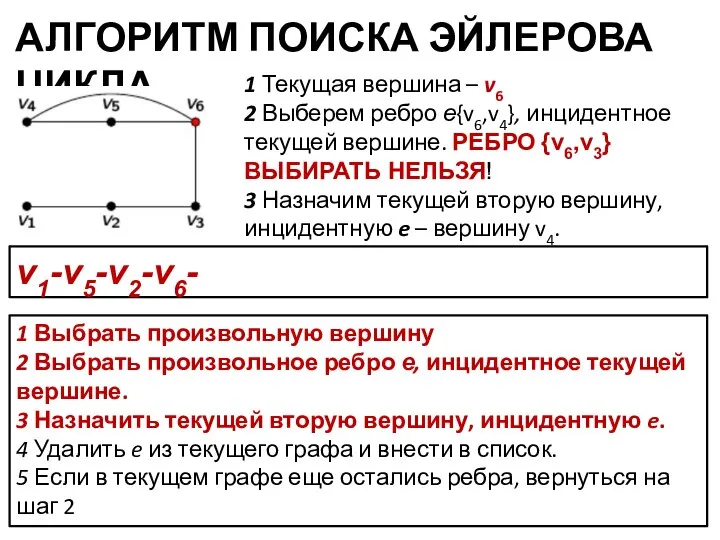
- 14. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
- 15. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
- 16. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
- 17. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
- 18. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
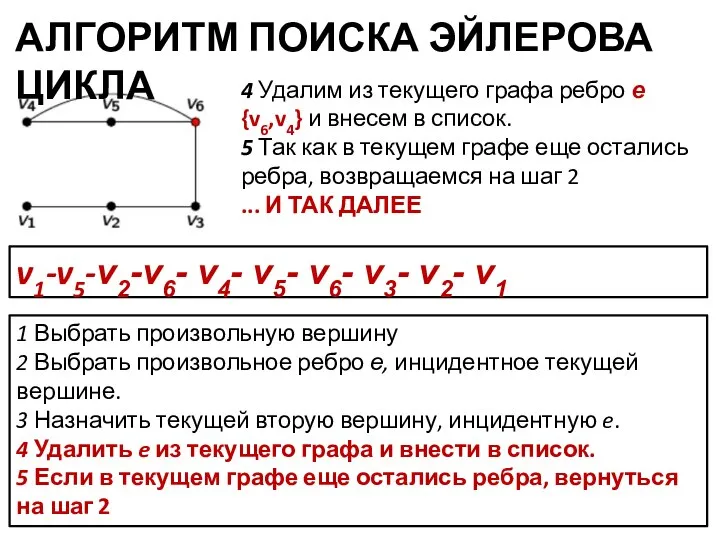
- 19. АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине.
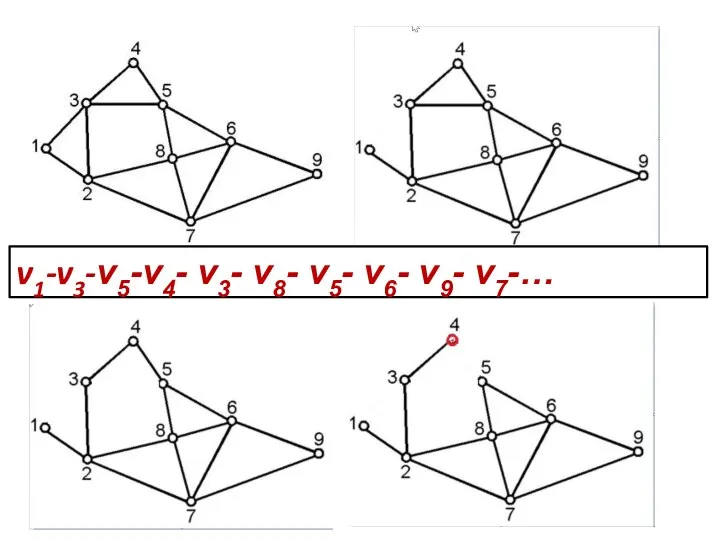
- 20. v1-v3-v5-v4- v3- v8- v5- v6- v9- v7-…
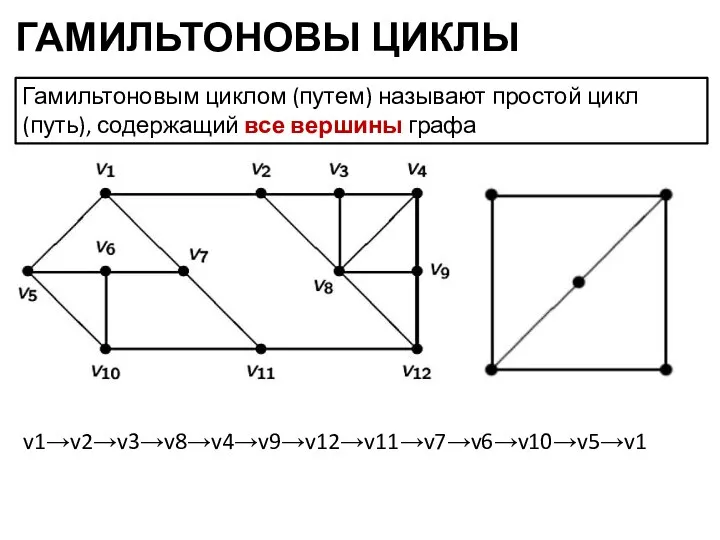
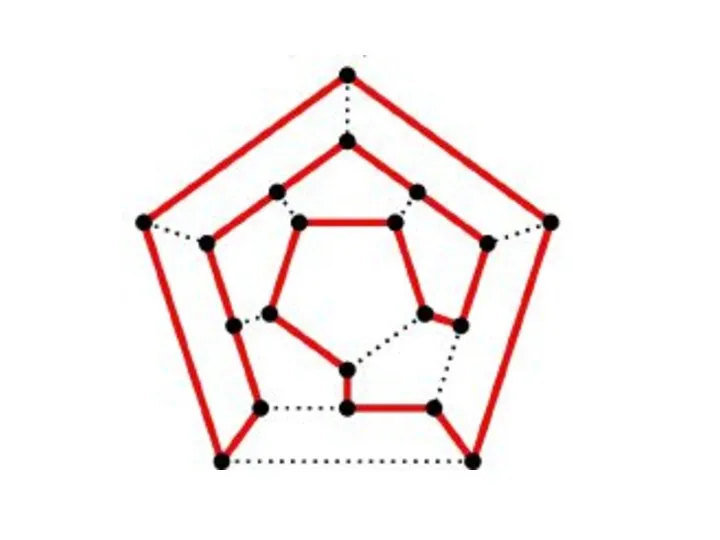
- 21. ГАМИЛЬТОНОВЫ ЦИКЛЫ Гамильтоновым циклом (путем) называют простой цикл (путь), содержащий все вершины графа v1→v2→v3→v8→v4→v9→v12→v11→v7→v6→v10→v5→v1
- 22. Задача коммивояжера разрешима тогда и только тогда, когда граф этой задачи гамильтонов. Задача коммивояжера: Дан список
- 23. СРАВНЕНИЕ ЗАДАЧ ОБ ЭЙЛЕРОВЫХ И ГАМИЛЬТОНОВЫХ ЦИКЛАХ Для решения вопроса о существовании эйлерова цикла в графе
- 24. Есть несколько достаточных условий существования гамильтоновых циклов в графе: 1. Всякий полный граф является гамильтоновым, так
- 29. Контрольные вопросы: Дайте определение эйлерова графа. Сформулируйте алгоритм построения эйлерова цикла. Какой граф называют гамильтоновым? Существует
- 30. Источники информации Программирование, компьютеры и сети https://progr-system.ru/
- 32. Скачать презентацию










 Комплексные числа и действия над ними
Комплексные числа и действия над ними Цена деления и предел измерения линейки
Цена деления и предел измерения линейки Состав чисел
Состав чисел Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу
Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу Реши уравнения
Реши уравнения Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Треугольники
Треугольники Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Решение уравнений с одной переменной
Решение уравнений с одной переменной Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Признаки параллельности прямых
Признаки параллельности прямых Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Математика. Числа до 20
Математика. Числа до 20 Какой функции соответствует график
Какой функции соответствует график Контрольная работа
Контрольная работа Теория антагонистических игр. Задачи для выполнения
Теория антагонистических игр. Задачи для выполнения Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Задачи на перебор вариантов
Задачи на перебор вариантов Решение тригонометрических уравнений
Решение тригонометрических уравнений Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора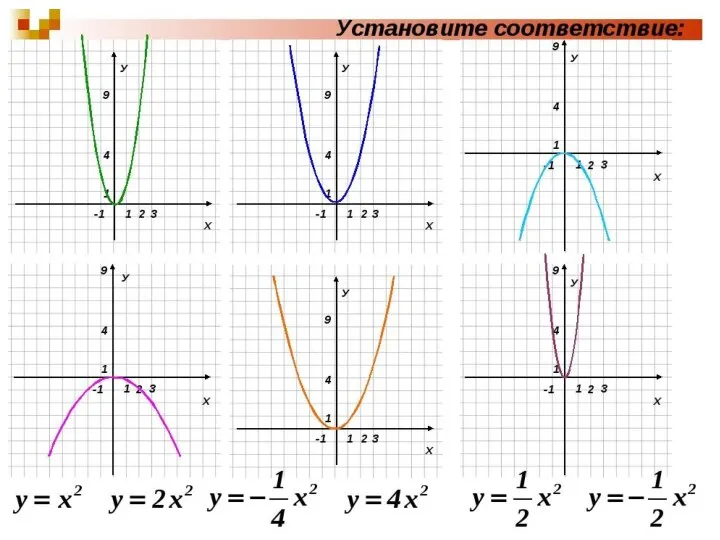 Графики функций
Графики функций Результант. Литература
Результант. Литература Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла