Содержание
- 3. Содержание: 1. План 2. Введение 3. Основная часть 4. Заключение 5. Общие выводы по работе 6.
- 4. План: 1. Введение. 2. Историческая справка. 3. Уравнения. Алгебраически уравнения. а) Основные определения. б) Линейное уравнение
- 5. Математика... выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного. Аристотель
- 6. Введение Данная работа является попыткой обобщить и систематизировать изученный материал по выше указанной теме. Мы расположили
- 7. Цель: Определить какие способы чаще всего применяются для решения уравнений. Задачи: Показать необходимость применения различных способов
- 8. Историческая справка: Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач
- 9. Уравнения. Алгебраические уравнения В алгебре рассматриваются два вида равенств – тождества и уравнения.
- 10. Тождество – это равенство, которое выполняется при всех (допустимых) значениях входящих в него переменных ). Для
- 11. Уравнение – это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие
- 12. Линейным уравнением называется уравнение первой степени. (1) где a и b – некоторые действительные числа. Линейное
- 13. Алгебраическое уравнение второй степени. (3) где a, b , c – некоторые действительные числа, называется квадратным
- 14. Уравнения n-й степени вида (8) называется двучленным уравнением. При a >0 и b >0 решается заменой
- 15. Алгебраическое уравнение четвертой степени. где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой
- 16. Рациональным алгебраическим уравнением называется уравнение вида (17) где и - многочлены. Далее для определенности будем полагать,
- 17. Уравнение, содержащее неизвестное (либо рациональное алгебраическое выражение от неизвестного) под знаком радикала, называют иррациональным уравнением. В
- 18. Приведем некоторые стандартные, наиболее часто применяемые методы решения Одним из самых простых является метод освобождения от
- 19. Множество допустимых значений этого уравнения: Положив , после подстановки получим уравнение или эквивалентное ему уравнение которое
- 20. Решая эти уравнения, находим, что данное иррациональное уравнение имеет единственный корень х=2. В заключение заметим, что
- 21. Заключение Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются
- 22. Общие выводы по работе Математика содержит множество способов и подходов к решению уравнений. В школьном курсе
- 23. Список использованной литературы 1. Глав. ред. М. Д. Аксенова. Энциклопедия для детей. Том 11. Математика. –
- 25. Скачать презентацию






















 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Величины. Длина
Величины. Длина Случайные величины 14 сен
Случайные величины 14 сен Возникновение первых математических понятий
Возникновение первых математических понятий Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс
Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс Умножение на 1 и 0
Умножение на 1 и 0 Диктант по геометрии
Диктант по геометрии Выбор схемы измерения переменных
Выбор схемы измерения переменных Умножение на 10,100,1000, 0,1, 0,01, 0,001
Умножение на 10,100,1000, 0,1, 0,01, 0,001 Подготовка к блиц-турниру
Подготовка к блиц-турниру Скалярное прозведение векторов
Скалярное прозведение векторов Шифр Цезаря
Шифр Цезаря Сфера и шар
Сфера и шар Многогранники. Призма
Многогранники. Призма Пропорции и проценты
Пропорции и проценты Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число Графический диктант
Графический диктант Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника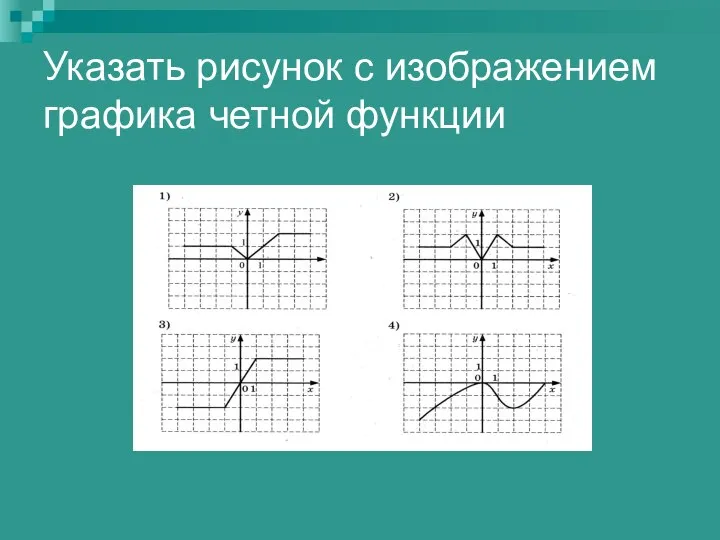 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Параллелепипед
Параллелепипед Выражение отношения в процентах
Выражение отношения в процентах Задачи на проценты. Схемы
Задачи на проценты. Схемы Решение нелинейных уравнений
Решение нелинейных уравнений Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика