Логика высказываний. Таблица истинности логических союзов

В качестве особой науки формальная логика (от греч. logos – слово, понятие, рассуждение, разум) существует около двух с половиной тысяч лет. Ее основателем считается великий древнегреческий мыслитель Аристотель (384–322 гг. до н.э.). В настоящее время эта наука представляет собой разветвленную дисциплину, включающую десятки разделов (теорий), которые приспособлены к применению в самых разнообразных областях человеческой деятельности.

Для гуманитарной сферы знаний особый интерес представляет раздел логики, предметом которого являются логические схемы (логической формы) естественных рассуждений, то есть рассуждений, фиксируемых и сообщаемых преимущественно средствами разговорного (естественного) языка.

Под рассуждением понимается связный, последовательный, непротиворечивый переход от одних мыслей к другим при рассмотрении некоторого предмета. Связные, цельные и осмысленные тексты (письменные, устные) – это, в конечном счете, более или менее сложные рассуждения. Рассудок – собирательное понятие для различного рода рассуждений.

Фундаментальный и наиболее простой раздел двухзначной логики – логика высказываний.
Он получил название от своей коренной категории – высказывания, то есть языкового выражения, о котором можно сказать только одно из двух: истинно оно или ложно.

Вопросы, просьбы, молитвы, приказы, восклицания не являются высказываниями. Например, о вопросе «Существовала ли Атлантида?» можно сказать, что он корректен (правильно поставлен), но не истинен; поэтому он – не высказывание. Не являются высказываниями отдельные слова (кроме случаев, когда они выступают представителями высказываний – «Ночь. Улица. Фонарь. Аптека. Бессмысленный и тусклый свет» (А.Блок)).

Логика высказываний, как и любой другой раздел формальной логики, имеет дело не столько с самими высказываниями, сколько со схемами их построения.
Предметный язык схем включает:
1) p, q, r, s, … – символы, которые обозначают переменные для простых высказываний;

2) ¬, ∧, ∨, →, ↔ - символы для обозначения логических союзов, связывающих переменные (в естественном языке им последовательно соответствуют выражения: «неверно, что», «и», «или», «если…, то», «если, и только если…, то» или их синонимы);
(, ) – скобки как указатели совершения логических действий.

На предметном уровне логические схемы построения высказываний (как и сами высказывания) делятся на простые и сложные. Сложную схему можно разбить на простые. Простая схема дальше не расчленяется.
Например, логическую схему p∧q (ей может соответствовать, например, высказывание «Полоцк – один из самых древних городов Беларуси, а Новополоцк – один из самых юных») можно разбить на две простых схемы – p и q. Поэтому это сложная схема.

Каждая из схем состоит из логических переменных и логических постоянных. Последние называются логическими союзами. Важнейшие из логических схем в логике высказываний – отрицание, конъюнкция, дизъюнкция (слабая и сильная), импликация, эквиваленция.

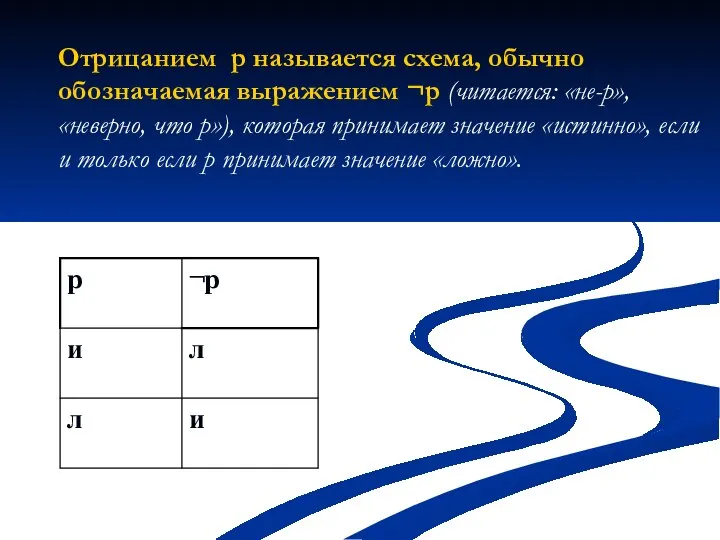
Отрицанием p называется схема, обычно обозначаемая выражением ¬p (читается: «не-p», «неверно, что p»), которая принимает значение «истинно», если и только если p принимает значение «ложно».

Конъюнкция p и q – логическая схема, обычно обозначаемая выражением p∧q, которая принимает значение «истинно», если и только если значение истинно принимает как p, так и q.
Выражение p∧q будем читать: «p и q».

Дизъюнкция слабая p и q – логическая схема, обычно обозначаемая выражением p∨q, которая принимает значение «истинно», если и только если значение «истинно» принимает хотя бы одно из p и q.
Выражение p∨q будем читать: «p или q».

Дизъюнкциия сильная p и q - логическая схема, обычно обозначаемая выражением p∨q, которая принимает значение «истинно», если и только если значение «истинно» принимает лишь одно из p и q.
Выражение p∨q будем читать: «либо p, либо q».

Импликация p и q – логическая схема, обычно обозначаемая выражением p→q, которая принимает значение «ложно», если и только если p принимает значение «истинно», а q – значение «ложно».
Выражение p→q будем читать: «если p, то q»,

Эквиваленция p и q – логическая схема, обычно обозначаемая выражением p↔q, которая принимает значение «истинно», если и только если значения p и q совпадают .
Выражение p↔q будем читать: «p, если и только если q», «p эквивалентно q».