Содержание
- 2. Лемма: Если векторы а и b коллинеарны и а ≠ 0, то существует такое число k,
- 5. Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
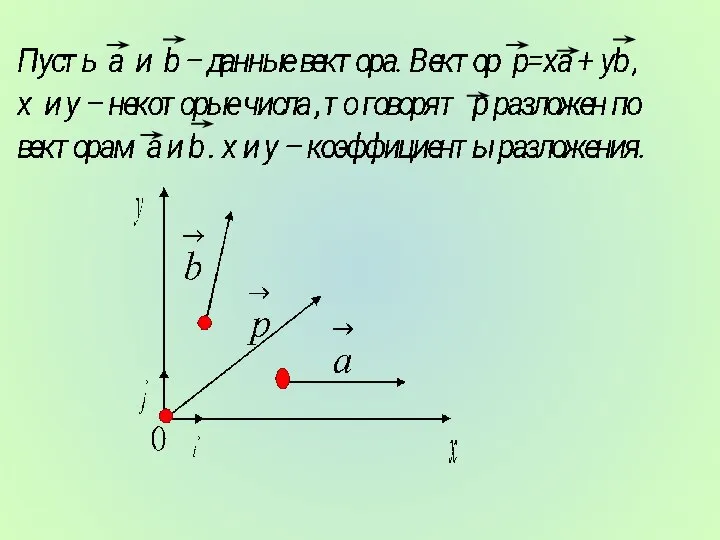
- 6. Доказательство: Пусть а и b - неколлинеарные векторы. Докажем , что любой вектор р можно разложить
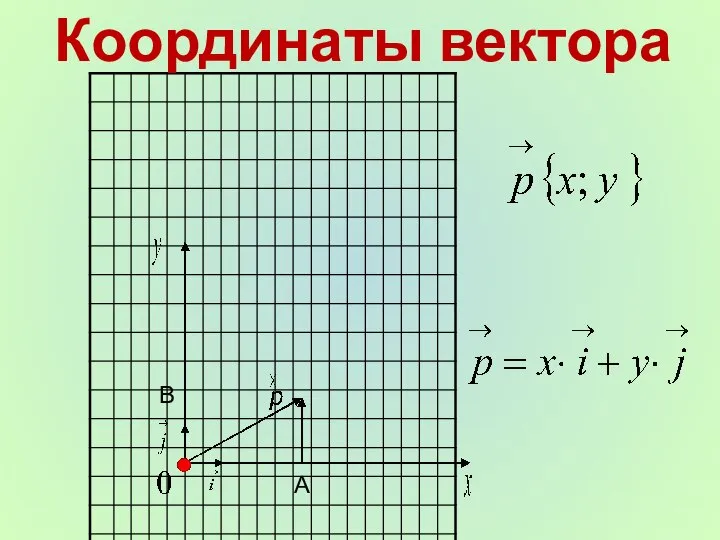
- 7. Координаты вектора А В
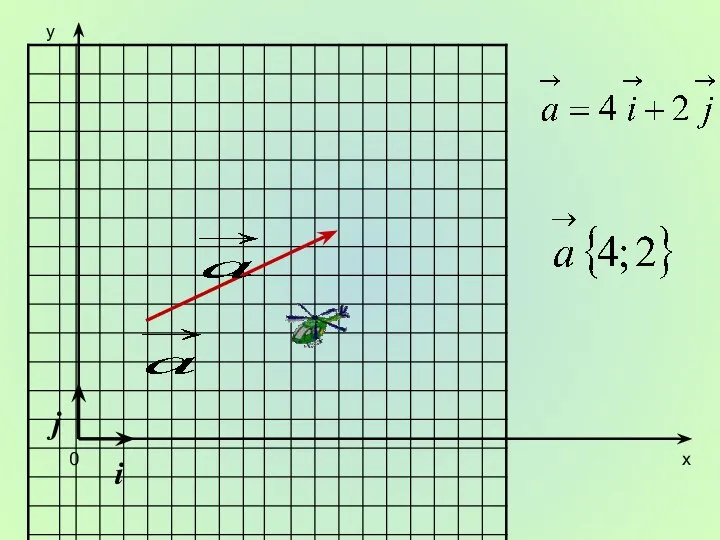
- 8. x y 0 i j
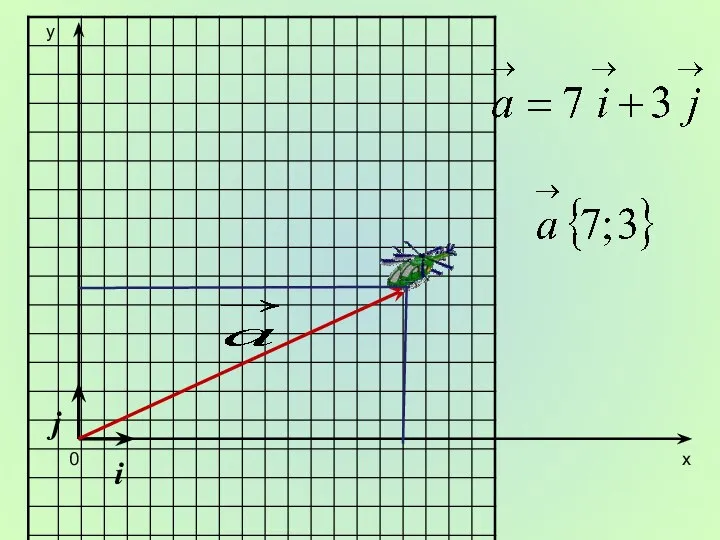
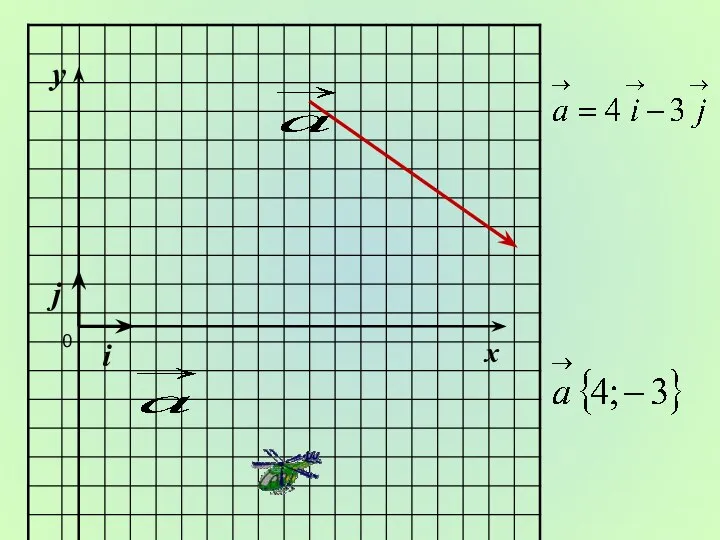
- 9. x y 0 i j
- 10. x y 0 i j
- 12. Скачать презентацию

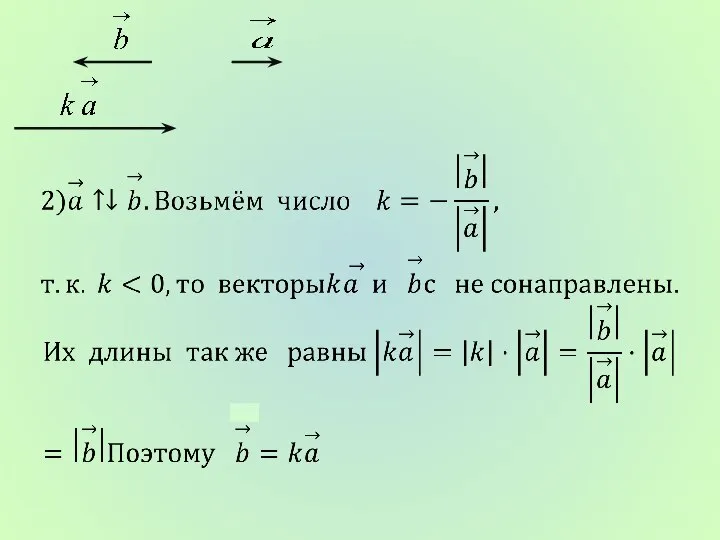


 Методика изучения площади
Методика изучения площади Векторы в пространстве
Векторы в пространстве Распределительный закон
Распределительный закон Четырехугольники
Четырехугольники Презентация на тему Занимательно о математике. Древняя нумерация, старинные меры длины, интересные цифры
Презентация на тему Занимательно о математике. Древняя нумерация, старинные меры длины, интересные цифры  Основные постулаты
Основные постулаты Reshenie_zadach_Gemetria_10
Reshenie_zadach_Gemetria_10 Цилиндры фараона
Цилиндры фараона Урок математики 14 декабря. Классная работа
Урок математики 14 декабря. Классная работа Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Набрать код доступа
Набрать код доступа Признаки параллельности прямых
Признаки параллельности прямых Параллельные плоскости
Параллельные плоскости Интерполирование с кратными узлами
Интерполирование с кратными узлами Треугольник и его виды
Треугольник и его виды Задачи на проценты
Задачи на проценты Этапы Всероссийской олимпиады школьников по математике: особенности задач, основные ошибки
Этапы Всероссийской олимпиады школьников по математике: особенности задач, основные ошибки Множества и операции над ними
Множества и операции над ними Теорема Пифагора
Теорема Пифагора Вычитание. Решение текстовых задач с помощью сложения и вычитания
Вычитание. Решение текстовых задач с помощью сложения и вычитания Задача на движение
Задача на движение Развертка, площадь боковой и полной поверхности пирамиды и усеченной пирамиды
Развертка, площадь боковой и полной поверхности пирамиды и усеченной пирамиды Презентация по математике "Отношение больше, меньше" -
Презентация по математике "Отношение больше, меньше" -  Производная функции
Производная функции Особенности решения 22 задания (часть С) в ОГЭ - математика. Средняя скорость - это не среднее арифметическое чисел
Особенности решения 22 задания (часть С) в ОГЭ - математика. Средняя скорость - это не среднее арифметическое чисел Выполни задания в электронном дневнике
Выполни задания в электронном дневнике Презентация на тему Обыкновенные дроби
Презентация на тему Обыкновенные дроби  Математические ребусы
Математические ребусы