Слайд 2Неполные квадратные уравнения вида
х2 = ɑ
нужно решать используя формулу сокращенного

умножения и утверждение «Произведение равно нулю, тогда и только тогда, когда хотя бы один из множителей равен нулю».
Слайд 4Напомню:
Уравнение – это равенство двух выражений, содержащее неизвестную.
Корень уравнения – это

значение неизвестного, при котором уравнение становится верным числовым равенством.
Решить уравнение – это значит найти все его корни или доказать, что их нет.
Слайд 5Для решения уравнений используют равносильны и неравносильные преобразования.
Равносильные преобразования:
1) Если к левой

и провой части уравнения прибавить одно и тоже число, то получим равносильное уравнение.
2) Если левую и правую часть уравнения умножить или разделить на одно и тоже число, то получим равносильное уравнение.
Слайд 6Неравносильные преобразования:
1) Умножение уравнения на выражение содержащее неизвестную (используется для избавления от

знаменателя).
2) Возведение в степень.
Слайд 7Неравносильные преобразования приводят уравнение к уравнению следствию. Значит нужно проводить проверку или

находить область допустимых значений (ОДЗ).
Поэтому решая простые уравнения, такие как неполные квадратные уравнения, нужно использовать равносильные преобразования.






 Геометрия. Планиметрия
Геометрия. Планиметрия Теорема синусов
Теорема синусов Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Математика и режим дня
Математика и режим дня Умножение десятичных дробей
Умножение десятичных дробей Линейная функция. 7 класс
Линейная функция. 7 класс Прямоугольный параллелепипед
Прямоугольный параллелепипед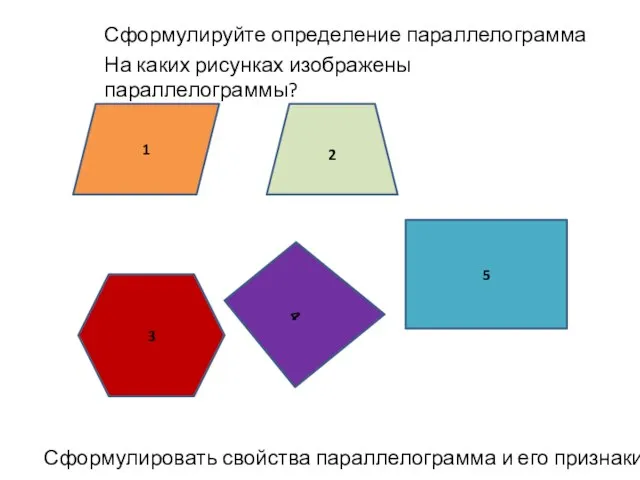 Презентация на тему Параллелограмм и трапеция (8 класс)
Презентация на тему Параллелограмм и трапеция (8 класс)  Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Сумма п-первых членов арифметической прогрессии
Сумма п-первых членов арифметической прогрессии Симплекс метод. Лекция 5
Симплекс метод. Лекция 5 Центральные углы
Центральные углы Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Координаты вектора. Простейшие задачи в координатах
Координаты вектора. Простейшие задачи в координатах Скалярное произведение в евклидовом и унитарном пространстве
Скалярное произведение в евклидовом и унитарном пространстве Презентация на тему РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ
Презентация на тему РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ  Базіс лінейнай прасторы. Каардынаты
Базіс лінейнай прасторы. Каардынаты Презентация на тему Конусы в нашей жизни
Презентация на тему Конусы в нашей жизни  Площадь многоугольника
Площадь многоугольника Основные комбинаторные конфигурации
Основные комбинаторные конфигурации История дробей
История дробей Тетраэдр
Тетраэдр Геометриялық фигуралар
Геометриялық фигуралар Решение системы уравнений первой степени с двумя неизвестными
Решение системы уравнений первой степени с двумя неизвестными Дроби и проценты. Построение диаграмм
Дроби и проценты. Построение диаграмм Математический калейдоскоп Областная интеллектуальная игра
Математический калейдоскоп Областная интеллектуальная игра Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики